光流（optical flow）和openCV中实现

转载请注明出处！！！http://blog.csdn.net/zhonghuan1992

光流（optical flow）和openCV中实现

光流的概念：

       是Gibson在1950年首先提出来的。它是空间运动物体在观察成像平面上的像素运动的瞬时速度，是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息的一种方法。一般而言，光流是由于场景中前景目标本身的移动、相机的运动，或者两者的共同运动所产生的。

         当人的眼睛观察运动物体时，物体的景象在人眼的视网膜上形成一系列连续变化的图像，这一系列连续变化的信息不断“流过”视网膜（即图像平面），好像一种光的“流”，故称之为光流（optical flow）。光流表达了图像的变化，由于它包含了目标运动的信息，因此可被观察者用来确定目标的运动情况。

         看下面的图，它展示了一个小球在5个连续的帧中的运动，箭头上的数字代表不同的帧，那个红色小球的运动构成了光流。

        

 

 

操作：

         给你一个图上的一系列点，在另外一张图上找到与前面一些列点相同的点。

         或者给你图I1上的点[u_x, u_y]^T，找到I2上的点[u_x + δ_x, u_y + δ_y]^T，最小化ε：

                  

         上面加入W_x表示一块区域，一般跟踪一个区域的点。

         在图形学应用中，在多张图上跟踪点（特征）是一项基本的操作：在一张图上找到一个对象，观察对象如何移动。

         基于特征点的跟踪算法大致可以分为两个步骤：

     1）探测当前帧的特征点；

     2）通过当前帧和下一帧灰度比较，估计当前帧特征点在下一帧的位置；

     3）过滤位置不变的特征点，余下的点就是目标了。

         特征点可以是Harris角点，也可以是边缘点等等。

         考虑一个像素在第一帧的光强度（这里增加了一个维度时间，前面的时候我们只是处理图像，所以没有必要时间。现在需要增加这个维度）。它移动了 的距离到一下帧，用了时间。因为像素点是一样的，光强度也没有发生变化（其实这个光强度没有改变是很多光流算法的基本假设）。，所以我们可以说：

然后通过泰勒级数近似展开有：

所以：

         上面的等式叫做光流等式，偏导数可以求出来，可是 u和v是未知的，所以无法解决上的等式。但是有很多方法可以解决这个问题，其中一个叫做Lucas-Kanade方法。

Lucas-Kanade：

         有这么一个假定，所有的相邻像素有相似的行动，Lucas-Kanade方法使用3*3的一块区域，它假定这9个点有相同的行动，所以现在的问题变为有9个等式，2个未知量，这个问题当然能够解决。一个好的解决方式是使用最小二乘法。

         令n=9，于是便有了9个等式：

  

         其中q1，q2，…，代表像素点，  是偏导，上面的等式可以写成下面的形式：A v = b，其中：

         然后，得到下面的：

         最终算出来的两个未知数的解是：

         上面的解决小而连贯的运动，想想刚刚我们的假设是9个像素点速度一致。因为现实中大而连贯的运动是普遍存在的，我们需要大的窗口来捕获运动，可是大窗口违背了运动连贯的假设，图像金字塔可以解决这个问题。（图像金字塔的内容以后本人掌握更多的再补充，现在不敢乱发表）。

OpenCV中的实现:

         OpenCV提供了对上面介绍的方法的支持，函数名叫做：cv2.calcOpticalFlowPyrLK()，现在让我们在视频中跟踪一些点。为了决定跟踪哪些点，使用cv2.goodFeaturesToTrack()。 

我们得到第一帧，探测Shi-Tomasi角点，然后我们使用 Lucas-Kanade光流法来跟综这些点。

#include "opencv2/video/tracking.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
 
#include 
#include 
 
using namespace cv;
using namespace std;
 
static void help()
{
    // print a welcome message, and the OpenCV version
    cout << "\nThis is ademo of Lukas-Kanade optical flow lkdemo(),\n"
        "Using OpenCVversion "<< CV_VERSION << endl;
    cout << "\nIt usescamera by default, but you can provide a path to video as an argument.\n";
    cout << "\nHot keys:\n"
        "\tESC - quitthe program\n"
        "\tr -auto-initialize tracking\n"
        "\tc - deleteall the points\n"
        "\tn - switch the\"night\" mode on/off\n"
        "To add/removea feature point click it\n" << endl;
}
 
Point2f point;
bool addRemovePt = false;
 
static void onMouse(int event, int x, int y, int /*flags*/, void* /*param*/)
{
    if (event == CV_EVENT_LBUTTONDOWN)
    {
        point = Point2f((float)x, (float)y);
        addRemovePt = true;
    }
}
 
int main(int argc, char** argv)
{
    help();
 
    VideoCapture cap;
    TermCriteria termcrit(CV_TERMCRIT_ITER | CV_TERMCRIT_EPS, 20, 0.03);
    Size subPixWinSize(10, 10), winSize(31, 31);
 
    const int MAX_COUNT = 500;
    bool needToInit = false;
    bool nightMode = false;
 
    /*if (argc == 1 || (argc == 2 && strlen(argv[1])== 1 && isdigit(argv[1][0])))
        cap.open(argc == 2 ? argv[1][0] - '0' :0);
    else if (argc == 2)
        cap.open(argv[1]);*/
 
    cap.open("G:\\视频分析入门练习\\视频分析入门练习 - 附件\\sample.avi");
 
    if (!cap.isOpened())
    {
        cout << "Could notinitialize capturing...\n";
        return 0;
    }
 
    namedWindow("LK", 1);
    setMouseCallback("LK", onMouse, 0);
 
    Mat gray, prevGray, image;
    vector points[2];
 
    for (;;)
    {
        Mat frame;
        cap >> frame;
        if (frame.empty())
            break;
 
        frame.copyTo(image);
        cvtColor(image, gray, COLOR_BGR2GRAY);
 
        if (nightMode)
            image = Scalar::all(0);
 
        if (needToInit)
        {
            // automaticinitialization
            goodFeaturesToTrack(gray, points[1],100, 0.01, 10, Mat(), 3, 0, 0.04);
            cornerSubPix(gray, points[1],subPixWinSize, Size(-1, -1), termcrit);
            addRemovePt = false;
        }
        else if(!points[0].empty())
        {
            vector status;
            vector err;
            if (prevGray.empty())
                gray.copyTo(prevGray);
            calcOpticalFlowPyrLK(prevGray, gray,points[0], points[1], status, err, winSize,
                3, termcrit, 0, 0.001);
            size_t i, k;
            for (i = k = 0; i  tmp;
            tmp.push_back(point);
            cornerSubPix(gray, tmp, winSize,cvSize(-1, -1), termcrit);
            points[1].push_back(tmp[0]);
            addRemovePt = false;
        }
 
        needToInit = false;
        imshow("LK", image);
 
        char c = (char)waitKey(100);
        if (c == 27)
            break;
        switch (c)
        {
        case 'r':
            needToInit = true;
            break;
        case 'c':
            points[0].clear();
            points[1].clear();
            break;
        case 'n':
            nightMode = !nightMode;
            break;
        }
 
        std::swap(points[1], points[0]);
        cv::swap(prevGray, gray);
    }
 
    return 0;
}

 

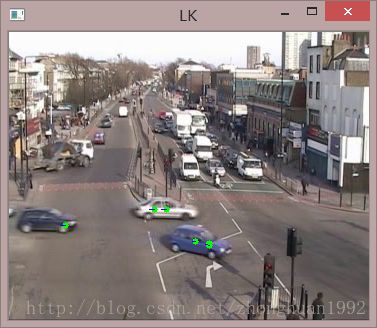
结果：随意取得一些特征点，特征点会随着车的移动而移动