早在上世纪七十年代末,Williams在他的“Casting Curved Shadows on Curved Surface”一文中提出了名为Shadow Map的阴影生成技术。之后,他人在此基础上针对相关问题做了许多改进。现在,Shadow Map仍被作为主流的阴影生成技术被广泛应用。
Z缓冲在一开始就是Shadow Map技术的实现基础。讨论Shadow Map技术的意义,不仅在于了解一种阴影生成技术,还在于可借此掌握一种很有用的技术手段。物体表面上一点,只有在与光源之间没有障碍阻隔时,它的深度值 才会被保存到Z缓冲中。换个角度看,这就相当于,在物体表面上某点的深度值被保存到Z-Buffer之前,用此点与光源间连线与场景中所有对象做了一次碰 撞检测。借用Z-Buffer做碰撞检测的这一方法,还可以用来帮助处理许多其它问题。
一、Shadow Map 原理
Shadow Map实际上比阴影体的原理要简单一些。阴影体是借助Stencil Buffer来做碰撞(观察者视线与阴影体中可能存在的障碍物之间),而Shadow Map则借助Z-Buffer来做碰撞检测。
图 一
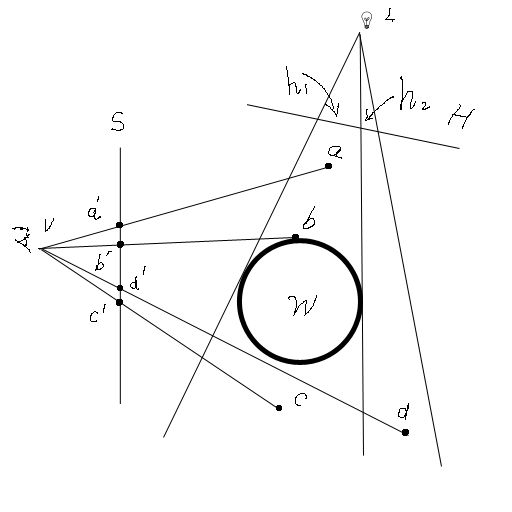
如图一所示,假设三维空间中,有物体W在光源L照射下形成阴影。空间中的a点位于W与L之间,c 点位于W之后,而b点是W表面上的一点。a、b、c、d经透视投影变换,在屏幕S上对应着a'、b'、c'、d'四个像素区域。
Shadow Map的思想方法是:假设先在光源L处放置一个摄像机(形成所谓的Light Space),则此像机将会把整个场景投影到相应的投影平面H上,其视锥在H平面上的投影是h1和h2两块区域之合。平面H所对应的Z-Buffer保存 的是Light Space的所有对象(本例中仅有W)的深度值。在实际生成观察平面S上的像素时,会先将像素对应的空间中的点(如上图中a'、b'、c'、d'所对应的 a、b、c、d)转换到Light Space中,投影到H平面上,并将相应的深度值与事先保存在H平面所对应的Z-Buffer的深度值进行比较,以图一为例,a点会投影到区域h1中,由 于它位于W之前,其深度值会比H平面的相应Z-Buffer中的值小;b点在h1上的投影点的深度值等于H平面的相应Z-Buffer中的值;c点在h1 上的投影点的深度值,则会大于H平面的相应Z-Buffer中的值;由于在生成H平面的投影时,会事先刷新其Z-Buffer的值,刷新值为1,所以在本 例中,空间d点在H上的投影的深度值也将小于相应点的Z-Buffer值;因此,通过空间中某一点在平面H上的投影的深度值与H平面原Z-Buffer中 的值的比较结果,就可以判断此点是否处于阴影中,并可根据这个判断来设置观察平面S上的相应像素的颜色。
考虑这样一种情况,空间中的一点如果处于观察者V的视锥中,同时又位于Light Space的视锥之外,那么显然就无法通过上面的方法来判断它是否被阴影所覆盖。这也是Shadow Map的局限之处。
Z-Buffer值一般由图形引擎结合相应硬件,在渲染管线内部计算,用户只需直接调用即可。因此直接使用Z-Buffer的值高效而又方便。 但是,通常情况下,Z-Buffer与Stencil Buffer合用4字节空间来描述一个像素,在Shadow Map中用来保存Light Space相应场景对象的深度值一般只有一个字节,而深度值是一个处于0~1之间的浮点数,这样势必会影响到后面的计算精度。这也可看作是传统 Shadow Map的另一不足。
绕过Z-Buffer来实现Shadow Map,可以为解决这一问题提供一种方法。
二、Shadow Map的实践
本文的实验是通过Fx Composer 2.5在一台 Laptop上进行的,其内置一块 nVidia GT420M显卡。
图 二
图 三
图二与图三是使用阴影前后的比较。这里没做镜面反射,处于影阴区的像素则被简单地直接涂黑。
首先要做的,是生成一张Shadow Map数据图。因为不使用Z-Buffer,就要做一些额外的创建工作,为了把DIY精神贯彻到底,索性一切从头开始。
1. 先来构建Light Space的相关转换矩阵
设置光源的位置和及Light Space的视锥投射方向:
1 float3 Lamp0Point = {0.0f,20.0f,0.1f};
2 float3 Lamp0LookAt = {0.0f,0.0f,0.0f};
1) 计算Light Space的View转换矩阵
设:
则根据仿射坐标系变换公式有:
![]()
其中,(xt, yt, zt) 为空间一点p在Light Space坐标系中的坐标;(xr, yr, zr)是点p在原世界坐标系中的坐标;M是原世界坐标系到Light Space坐标系的过渡矩阵;(x0, y0, z0)是Light Space坐标系原点在原世界坐标系中的坐标值。α1、 α2、 α3是Light Space坐标系的基向量,(a11, a12, a13)、(a21, a22, a23)、(a31, a32, a33)是三个坐标轴向量在原世界坐标系中坐标。
由上式可得:
![]()
由于直角坐标系基向量互为正交向量,所以有:
据此得到Light Space的View转换矩阵计算函数为:
1 float4x4 LightViewMat(float3 lampPos, float3 lampLookAt)
2 {
3 float3 lampDirt = lampLookAt - lampPos; 4 5 float3 vUp = float3(0.0f, 1.0f, 0.0f); 6 float3 vFront = normalize(lampDirt); 7 float3 vRight = cross(vUp, vFront); 8 vRight = normalize(vRight); 9 vUp = cross(vFront, vRight); 10 vUp = normalize(vUp); 11 12 // get the matrix from I to II 13 float4x4 matTrans = 14 { 15 1, 0, 0, 0, 16 0, 1, 0, 0, 17 0, 0, 1, 0, 18 -lampPos.x, -lampPos.y, -lampPos.z, 1, 19 }; 20 21 float4x4 matView = 22 { 23 vRight.x, vUp.x, vFront.x, 0, 24 vRight.y, vUp.y, vFront.y, 0, 25 vRight.z, vUp.z, vFront.z, 0, 26 0, 0, 0, 1, 27 }; 28 29 float4x4 mView = mul(matTrans, matView); 30 31 return mView; 32 }
2) 计算Light Space的投影矩阵
在设定了视锥体近裁剪平面和远裁剪平面的值后,根据给定的y方向的视角,就可以计算出投影平面上透视投影区域在y轴上的坐标范围(top值和 bottom值);再根据给出的宽高比(aspect),就可以方便地算出透视投影区域在x轴上的坐标范围(right值和left值)。透视投影矩阵的 目的是将视锥转换为x∈[-1,1],y∈[-1, 1],z∈[0, 1]长方体(CVV)。经透视投影矩阵处理后的空间坐标,还要再做一个齐次化处理(将x,y,z值分别除以w)。一个处于视锥体内的点经透视变换和齐次化 处理后,其坐标值必处于CVV体的范围内;一个处于视锥体外的点经透视变换和齐次化处理后,其坐标值必处于CVV体范围之外。这就是依靠CVV体进行裁剪 的算法依据。实际上,裁剪操作在经过透视矩阵的转换后,在做齐次化处理之前就完成了,这样做可以大大减少运算量。
对于透视变换来说,有了投影平面上的相应点的x、y值,就可以直接画出物体在透视投影后的形状。投影平面上的x、y值通过等比关系就可以计算得到。透视变 换后所得的点的z值,因为可以体现空间中各对象间的前后遮挡关系,所以也需要计算并保留下来。在实际计算时,由于要将处于视锥体内的各点的坐标范围转化到 CVV体中,故而要通过 z' = a*z+b这种方式(而不是直接依靠几何上的等比关系)构造出来。具体过程可以参看这两篇文章。对于Shadow Map来说,透视投影所得的Z值尤为重要。
1 float4x4 LightProjcetMat()
2 {
3 // get the matrix prjection 4 float yfov = 1.57f; // 90 degree 5 float aspect = ViewPortSize.x/ViewPortSize.y; 6 float n = 6.0f; 7 float f = 100.0f; 8 float dfn = f - n; 9 10 float t = 0.362*n*tan(yfov/2); 11 float b = -t; 12 float r = t*aspect; 13 float l = -r; 14 float drl = r - l; 15 float dtb = t - b; 16 float arl = r + l; 17 float atb = t + b; 18 19 float4x4 matProj = 20 { 21 2*n/drl, 0, 0, 0, 22 0, 2*n/dtb, 0, 0, 23 arl/drl, atb/dtb, f/dfn, 1, 24 0, 0, -f*n/dfn, 0, 25 }; 26 27 28 return matProj; 29 }
第10行在计算t值时,多乘了一个0.362的缩放因子(根据实际情况调整),目的在于减少生成Shadow Map时的计算误差。第6行将近裁剪平面设为6.0而不是常见的1.0,也可起到同样的作用。
3) 定义并生成Shadow Map纹理
1 texture2D Lamp0ShadowMapColor : RENDERCOLORTARGET
2 <
3 float2 ViewPortRatio = {1.0,1.0}; 4 int MipLevels = 1; 5 string Format = "A8R8G8B8" ; 6 >; 7 8 sampler2D Lamp0ShadowMapSampler = sampler_state { 9 Texture = ; 10 FILTER = MIN_MAG_MIP_LINEAR; 11 AddressU = Clamp; 12 AddressV = Clamp; 13 };
第3行的作用是使生成的Shadaow Map纹理大小与渲染窗口自动保持一致,这样可以很方便地观察到Shadow Map纹理大小改变时,对最终生成的阴影效果的影响。
1 float4x4 matWorld : World;
2 float4x4 matView : View;
3 float4x4 matProject : Projection; 4 5 struct SourceData 6 { 7 float3 pos3 : POSITION; 8 float4 n : NORMAL; 9 }; 10 11 struct VertexOutput 12 { 13 float4 pos4 : POSITION; 14 15 float4 rpos4 : TEXCOORD3; 16 float4 n : NORMAL; 17 18 float4 lpos4 : TEXCOORD2; 19 float4 ldirt4 : TEXCOORD6; 20 float4 uvd : TEXCOORD5; 21 }; 22 23 static float4x4 matLightView = LightViewMat(Lamp0Point, Lamp0LookAt); 24 static float4x4 matLightProj = LightProjcetMat(); 25 26 VertexOutput makeShadowVS(SourceData vData) 27 { 28 VertexOutput vOut = (VertexOutput)0; 29 30 float4x4 matTmp = mul(matWorld, matLightView); 31 matTmp = mul(matTmp, matLightProj); 32 33 34 float4 coordCVV = mul(float4(vData.pos3.xyz, 1.0f), matTmp); 35 36 float4 m = 1/coordCVV.w; 37 38 vOut.pos4.xyz = m*coordCVV.xyz; 39 vOut.pos4.w = 1.0f; 40 41 vOut.lpos4 = vOut.pos4; 42 vOut.lpos4.z *= fat; 43 44 return vOut; 45 } 46 47 float4 makeShadowPS(VertexOutput In) : COLOR 48 { 49 return float4(In.lpos4.z, 0, 0, 1); 50 }
在生成纹理时,将Z-Buffer Test 设为Enable状态,这样就可以保证纹理中保存的深度值始终是离光源最近的那个点的。另外,可以修改上段代码第5行的纹理像素格式,就能方便地得到更精确的深度值。
4) 使用Shadow Map纹理生成阴影
以图一为例,直观来看,生成阴影前应该先将相应观察平面S上的像素对应的空间点(如b'对应的b)的位置计算出来,再用之前生成的Light Space的matLightView和matLightProj把点b投射到平面H上。这样就需要进行从b'到b的变换,很显然观察窗口S的透视矩阵的 逆矩阵是存在的。但实际上还有更简易的做法:
1 VertexOutput useShadowVS(SourceData vData)
2 {
3 VertexOutput v = (VertexOutput)0; 4 v.pos4 = mul(float4(vData.pos3, 1.0f), matWorldViewProj); 5 6 7 v.n = mul(float4(vData.n.xyz, 0.0f), matWorld); 8 v.n = normalize(v.n); 9 v.rpos4 = mul(float4(vData.pos3, 1.0f), matWorld); 10 11 float3 vLightDirect = Lamp0Point - v.rpos4.xyz; 12 vLightDirect = normalize(vLightDirect); 13 v.ldirt4 = float4(vLightDirect, 0.0f); 14 15 float4x4 matTmp = mul(matWorld, matLightView); 16 matTmp = mul(matTmp, matLightProj); 17 18 float4 lightCVV = mul(float4(vData.pos3, 1.0f), matTmp); 19 lightCVV.z -= 0.1f; 20 21 float m = 1/lightCVV.w; 22 lightCVV.xyz = m*lightCVV.xyz; 23 lightCVV.w = 1.0f; 24 25 v.lpos4 = lightCVV; 26 27 28 float2 uv = (float2)0; 29 uv.x = (1.0f+v.lpos4.x)/2.0f; 30 uv.y = (1.0f-v.lpos4.y)/2.0f; 31 v.uvd.xy = uv; 32 v.uvd.z = v.lpos4.z; 33 34 return v; 35 } 36 37 38 float4 useShadowPS(VertexOutput v) : COLOR 39 { 40 41 float2 uv = v.uvd.xy; 42 float dep = v.uvd.z; 43 44 float3 samplerCol = (float3)0; 45 float c = -1; 46 float tmpLm = 0.0f; 47 48 float3 sdp = tex2D(Lamp0ShadowMapSampler, uv).rgb; 49 if( dep < sdp.x ) 50 { 51 tmpLm = 1.0f; 52 } 53 float fall = 1.0/dot(v.ldirt4.xyz, v.ldirt4.xyz); 54 55 float3 ld = v.ldirt4.xyz; 56 float3 n = v.n; 57 float diffuse = dot(ld, n); 58 float3 col = float3(1,1,1); 59 float linf = 0.8f; 60 //col = diffuse * col; 61 62 tmpLm = (tmpLm)*diffuse*fall*linf; 63 col = tmpLm * col; 64 65 return float4(col, 1); 66 }
第15到第32行,直接计算出每一个顶点在Light Space投影平面上的点的x、y、 z坐标值;在进入到观察者投影变换时,可见像素的x、y、z坐标就可以据此通过插值得到。这样做好处是,避免计算透视变换的逆运算,能使代码更简洁,不足 之处是增加了大量多余的运算。
第19行,对lightCVV的z值做了一个偏移运算,作用是校正浮点运算可能出现的误差。以图一中的点b为例,由于基于浮点数的空间变换运算会出现计 算误差,因此位于W表面上的b点经投影变换后,本应等于Z-Buffer中相应像素的深度值,有可能变得大于此值,从而导致其后的逻辑判断出错(第49 行),所以需要对运算结果做一个误差校正。更一般的做法是将lightCVV乘以一个事先设置好的误差校正矩阵。
第53行,计算光照强度衰减因子(与距离的平方成反比)。初始光照强度在第59行设定。