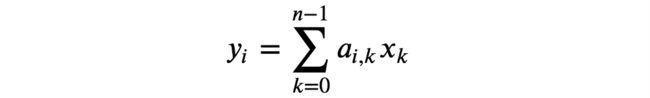Weight Initialization in Neural Networks: A Journey From the Basics to Kaiming
我想邀请您加入我的探索,通过不同的方法初始化神经网络中的图层权重。 通过各种简短的实验和思想练习,我们将逐步发现为什么在训练深度神经网络时足够的重量初始化非常重要。 在此过程中,我们将介绍研究人员多年来提出的各种方法,并最终深入研究最适合您最有可能使用的当代网络架构的方法。
接下来的例子来自我自己重新实现的一套笔记本,Jeremy Howard在最新版本的fast.ai的深度学习第二部分课程中介绍了这一课程,该课程目前于2019年春天在USF的数据研究所举行。
Why Initialize Weights
权重初始化的目的是防止层激活输出在正向通过深度神经网络的过程中爆炸或消失。如果发生任何一种情况,损失梯度将太大或太小而无法有效地向后流动,并且如果网络甚至能够这样做,则网络将花费更长时间来收敛。
矩阵乘法是神经网络的基本数学运算。在具有多个层的深度神经网络中,一个前向通道仅需要在每个层,在该层的输入和权重矩阵之间执行连续的矩阵乘法。在一层的这种乘法的乘积成为后续层的输入,依此类推。
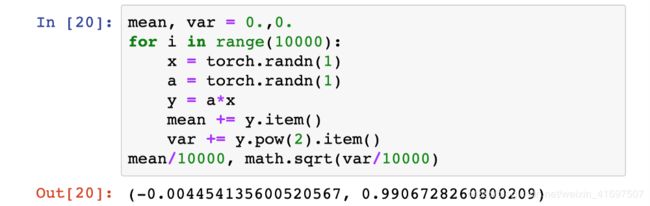
对于一个说明这一点的快速和肮脏的例子,让我们假设我们有一个包含一些网络输入的向量x。这是训练神经网络的标准做法,以确保我们的输入值被缩放,使得它们落入这样的正态分布,平均值为0,标准差为1。
![]()
让我们假设我们有一个没有激活的简单的100层网络,并且每个层都有一个包含图层权重的矩阵a。 为了完成单个前向传递,我们必须在层输入和每100个层中的权重之间执行矩阵乘法,这将使总共100个连续矩阵乘法。
事实证明,从我们对输入进行缩放的相同标准正态分布初始化图层权重值绝不是一个好主意。 为了了解原因,我们可以模拟我们假设网络的正向传递。
哇! 在这100次乘法期间的某个地方,层输出变得非常大,甚至计算机也无法识别它们的标准偏差并且意味着数字。 我们实际上可以确切地看到发生了多长时间。
激活输出在我们网络的29层内爆炸。 我们明确地将权重初始化为过大。
不幸的是,我们还要担心防止层输出消失。 为了看看当我们初始化网络权重太小时会发生什么 - 我们将扩展我们的权重值,使得它们仍然落入平均值为0的正态分布内,它们的标准偏差为0.01。
在上述假设的前向传递过程中,激活输出完全消失。
总结一下,如果权重被初始化得太大,网络将无法很好地学习。 当权重初始化太小时也会发生同样的情况。
How can we find the sweet spot?
请记住,如上所述,完成正向传递通过神经网络所需的数学只需要连续的矩阵乘法。 如果我们的输出y是我们的输入向量x和权重矩阵a之间的矩阵乘法的乘积,则y中的每个元素i被定义为
其中i是权重矩阵a的给定行索引,k是权重矩阵a中的给定列索引和输入向量x中的元素索引,并且n是x中元素的范围或总数。 这也可以在Python中定义为:
y[i] = sum([c*d for c,d in zip(a[i], x)])
我们可以证明,在给定的层,我们从标准正态分布初始化的输入x和权重矩阵a的矩阵乘积平均具有非常接近输入连接数的平方根的标准偏差, 在我们的例子中是√512。
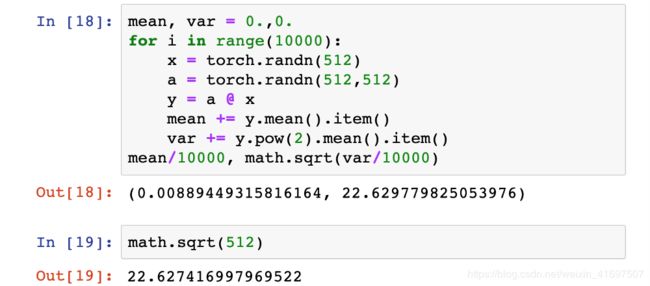
如果我们根据如何定义矩阵乘法来看这个属性就不足为奇了:为了计算y,我们将输入x的一个元素的元素乘法乘以权重a的一列的512个乘积相加。 在我们使用标准正态分布初始化x和a的示例中,这512个产品中的每一个的平均值为0,标准差为1。
然后,这512个产品的总和的平均值为0,方差为512,因此标准差为√512。
这就是为什么在上面的例子中我们看到我们的图层输出在29次连续矩阵乘法后爆炸。 在我们简单的100层网络架构的情况下,我们想要的是每层的输出具有大约1的标准偏差。这可以想象我们可以在我们想要的多个网络层上重复矩阵乘法 没有激活爆炸或消失。
如果我们首先通过将所有随机选择的值除以√512来对权重矩阵a进行缩放,那么填充输出y的一个元素的元素乘法现在平均只有1 /√512的方差。
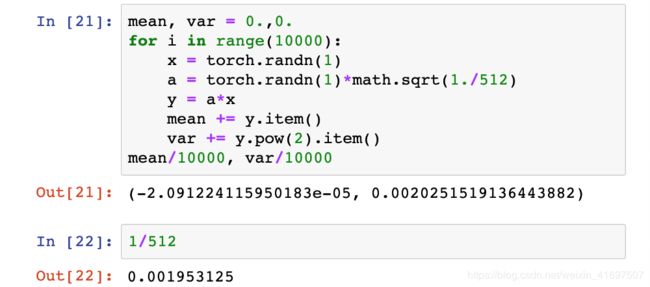
这意味着矩阵y的标准偏差(包含通过输入x和权重a之间的矩阵乘法生成的512个值中的每一个)将是1.让我们通过实验确认。
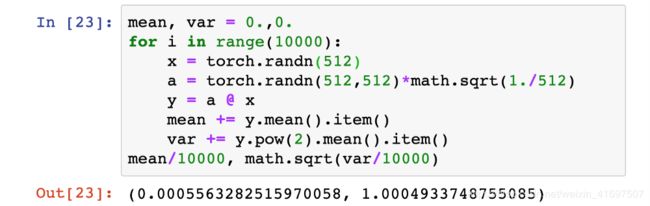
现在让我们重新运行我们快速而肮脏的100层网络。 和以前一样,我们首先从[-1,1]内的标准正态分布中随机选择层权重,但这次我们将这些权重按1 /√n进行缩放,其中n是一层的网络输入连接数,即 我们的例子中有512个。

成功! 即使在我们的100个假设层之后,我们的层输出既不会爆炸也不会消失。
虽然乍一看似乎在这一点上我们可以称它为一天,现实世界的神经网络并不像我们的第一个例子似乎表明的那么简单。 为简单起见,省略了激活功能。 但是,我们永远不会在现实生活中这样做。 这要归功于在网络层的尾端放置这些非线性激活函数,深度神经网络能够创建描述现实世界现象的复杂函数的近似近似,然后可用于生成令人惊讶的令人印象深刻的预测, 例如手写样本的分类。
Xavier Initialization
直到几年前,最常用的激活函数关于给定值是对称的,并且具有渐近接近从该中点加/减一定距离的值的范围。 双曲正切和softsign函数举例说明了这类激活。
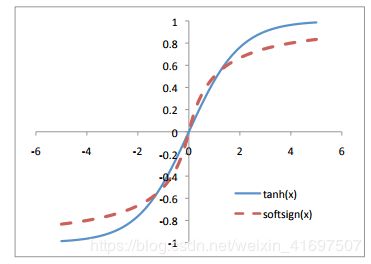
Tanh and softsign activation functions.
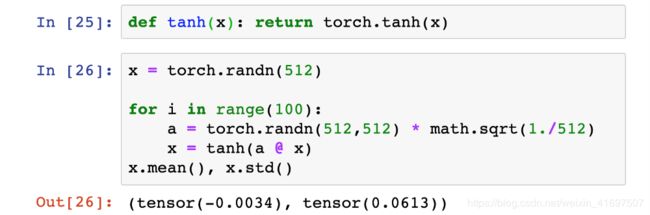
我们将在假设的100层网络的每一层之后添加一个双曲正切激活函数,然后看看当我们使用本土权重初始化方案时会发生什么,其中层权重按1 /√n缩放。
第100层的激活输出的标准偏差低至约0.06。 这绝对是偏小的一面,但至少激活并没有完全消失!
直观地说,发现我们自己的体重初始策略的旅程现在看起来似乎回想起来,你可能会惊讶地听到,就在2010年,这不是初始化体重层的传统方法。
当Xavier Glorot和Yoshua Bengio发表他们的标题性文章理解训练深度前馈神经网络的难度时,“常用的启发式” 他们比较了他们的实验是从[-1,1]中的均匀分布初始化权重,然后按1 /√n缩放。
事实证明,这种“标准”方法实际上并不能很好地发挥作用。
使用“标准”重量初始化重新运行我们的100层tanh网络会导致激活梯度变得无限小 - 它们就像消失一样好。
这种糟糕的表现实际上是促使Glorot和Bengio提出他们自己的权重初始化策略,他们在他们的论文中称之为“规范化初始化”,现在通常被称为“Xavier初始化”。
Xavier初始化将图层的权重设置为从在其间界定的随机均匀分布中选择的值
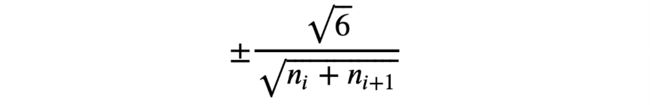
其中nᵢ是该层的传入网络连接数或“扇入”数,nᵢ₊1是该层的传出网络连接数,也称为“扇出”。
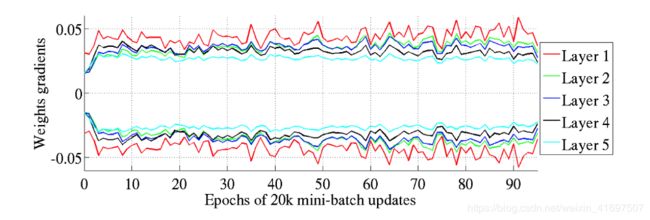
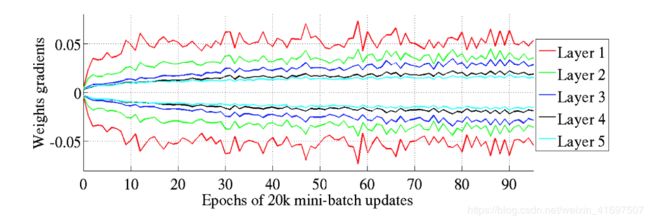
Glorot和Bengio认为Xavier权重初始化将保持激活和反向传播梯度的变化,一直向上或向下网络层。 在他们的实验中,他们观察到Xavier初始化使得5层网络能够在层间保持其重量梯度的几乎相同的方差。
相反,事实证明,使用“标准”初始化会在网络较低层的权重梯度与较高层的权重梯度之间的差异方面带来更大的差距,而最高层的权重梯度接近于零。
为了推动这一点,Glorot和Bengio证明了使用Xavier初始化的网络在CIFAR-10图像分类任务上实现了更快的收敛和更高的准确性。HTML)。
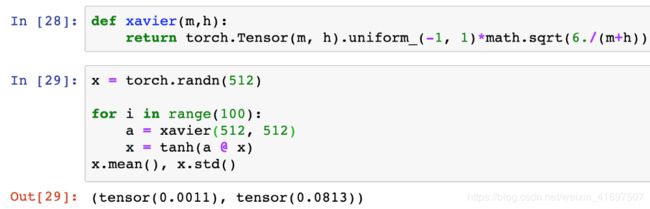
让我们再次重新运行我们的100层tanh网络,这次使用Xavier初始化:
在我们的实验网络中,Xavier初始化执行与我们之前导出的本地方法完全相同,我们从随机正态分布中采样值,并通过传入网络连接数n的平方根进行缩放。
Kaiming Initialization
从概念上讲,当使用关于零对称且在[-1,1]内有输出的激活函数(例如softsign和tanh)时,我们希望每层的激活输出的平均值为0和a 标准偏差大约为1,平均。 这正是我们的本土方法和Xavier所能实现的。
但是,如果我们使用ReLU激活功能呢? 想以同样的方式扩展随机初始权重值是否仍然有意义?
为了看看会发生什么,让我们在我们假设的网络层中使用ReLU激活而不是tanh,并观察其输出的预期标准偏差。
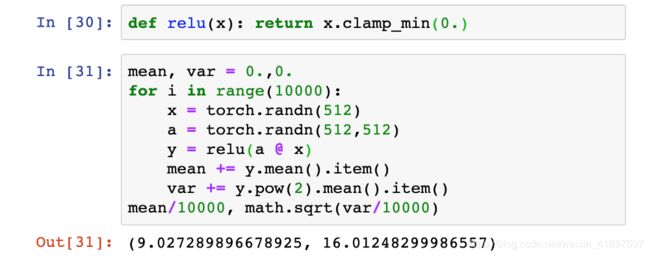
事实证明,当使用ReLU激活时,单个层的平均标准偏差将非常接近输入连接数的平方根,除以2的平方根,或√512/√2 例。

通过该数字缩放权重矩阵a的值将导致每个单独的ReLU层平均具有1的标准偏差。
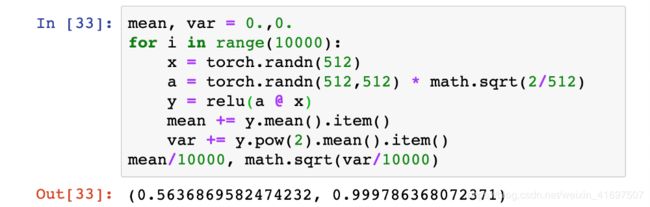
正如我们之前表明,饲养层激活的标准偏差约为1将使我们能够堆叠在一个很深的神经网络的几个多层无梯度爆炸或消失。
关于如何在具有类似ReLU的激活的网络中最佳地初始化权重的探索是Kaiming He等人的动机。人。为提出自己的初始化方案这是对于使用这类非对称,非线性的激活深层神经网络量身定制的。
在他们的2015年论文中,他等。人。证明了如果采用以下输入权重初始化策略,深层网络(例如22层CNN)会更早收敛:
- 创建适于在给定层的权重矩阵的尺寸的张量,并与来自标准正态分布随机选择的号码填充它。
- 通过√2/√N其中n是(也被称为“扇入”)进入来自先前层的输出的给定层的传入连接的数目乘以每个随机选择的数。
- 偏差张量初始化为零。
我们可以按照下列指示来实现我们自己的开明初始化的版本,并确认它确实可以防止激活输出从爆炸或者RELU在我们假想的100层网络的所有层使用消失。
作为最后的比较,如果我们使用Xavier初始化,那么将会发生这种情况。
哎哟! 当使用Xavier初始化权重时,激活输出几乎完全消失了第100层!
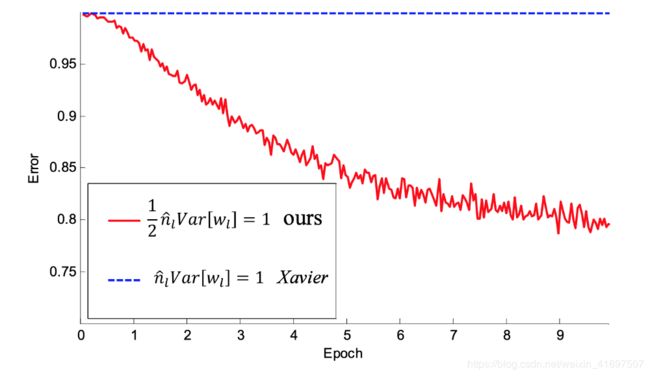
顺便提一下,当他们训练使用ReLU的更深层网络时,He等。人。 发现使用Xavier初始化的30层CNN完全停止并且根本没有学习。 然而,当根据上面概述的三步程序初始化相同的网络时,它获得了更大的收敛。
Kaiming init支持30层CNN的融合。
对我们来说,故事的寓意是,我们从头开始训练的任何网络,特别是计算机视觉应用,几乎肯定会包含ReLU激活功能,并且深层次。 在这种情况下,开明应该是我们的首选权重初始策略。
Yes, You Too Can Be a Researcher
更重要的是,当我第一次看到Xavier和Kaiming公式时,我并不羞于承认我感到害怕。对于他们各自的六,二的平方根源,我的一部分不禁感到他们一定是某种我无法自己理解的一种神秘智慧的结果。让我们面对它,有时深度学习论文中的数学看起来很像象形文字,除了没有[Rosetta Stone](https://en.wikipedia.org/ wiki / Rosetta_Stone)帮助翻译。
但我认为我们在这里所经历的旅程向我们表明,这种对恐吓感的下意识反应虽然完全可以理解,但绝不是不可避免的。虽然开明和(特别是)泽维尔的论文确实包含了他们公平的数学分享,但我们亲眼目睹了实验,经验观察和一些直截了当的常识如何足以帮助推导出支持目前最广泛的核心原则的核心原则。使用重量初始化方案。