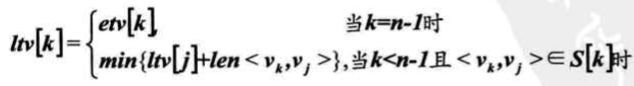数据结构 - 第六章 图
定义
图 (Graph) 是由顶点的有穷非空集合和顶点之间边的集合组成，结点之间存在多对多的关系。通常表示为：G ( V, E )。其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
简单图：不存在顶点到其自身的边，且同一条边不重复出现。
完全图：任意两个顶点之间都存在边。有向图中，要求两个顶点存在互相指向的边。
有向图：两顶点间的边有方向，用<>表示。
无向图：两顶点间的边无方向，用()表示。
稀疏图：有很少条边或弧的图，反之称为稠密图。
网：边或弧具有与它相关的数字的图，数字即权重。
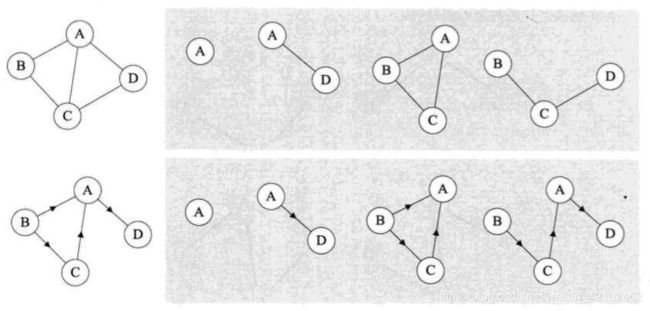
图与子图的关系，如下图所示。
路径：构成两点间通路的顶点序列，路径的长度是路径上的边或弧的数目。
环/回路：第一个顶点到最后一个顶点相同的路径。
连通图：图中任意两个结点都是连通的。
连通分量：无向图中的极大连通子图。
强连通分量：有向图中的极大强连通子图。
极小连通子图：连通图的生成树，它含有图中全部的n个顶点，但只有足以构成一棵树的 n-1 条边。非连通图的多棵生成树构成一个生成森林。
存储结构
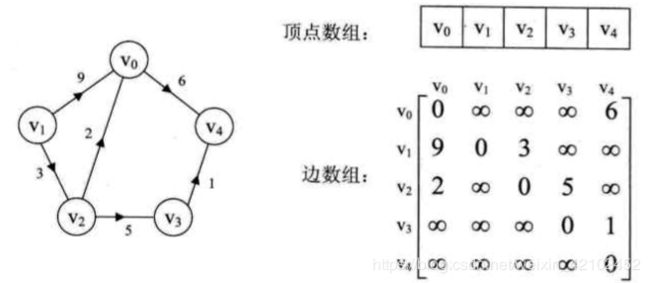
邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。适用于稠密图。
邻接表是一种数组与链表相结合的存储方法。适用于稀疏图。
1、图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。
2、图中每个顶点Vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点VI的边表，有向图则称为顶点Vi作为弧尾的出边表。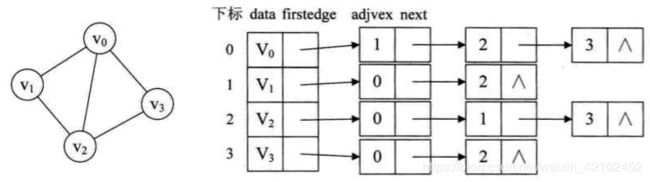
十字链表即有向图的邻接多重表，把邻接表与逆邻接表结合起来，同时关心了入度和出度的问题。
顶点的结点结构为
。其中firstin表示入边表头指针，指向该顶点的入边表中第一一个结点， firstout 表示出边表头指针，指向该顶点的出边表中的第一个结点。
边的结点结构为
。其中tailvex 是指弧起点在顶点表的下标，headvex 是指弧终点在顶点表中的下标，headlink 是指入边表指针域，指向终点相同的下一条边，taillink 是指边表指针域，指向起点相同的下一条边。如果是网，还可以再增加一个weight域来存储权值。
邻接多重表即无向图的邻接多重表，仿照了十字链表的格式。
边的结点结构为
。其中ivex和jvex是与某条边依附的两个顶点在顶点表中下标。ilink 指向依附顶点ivex的下一条边，jlink 指向依附顶点jvex的下一条边。
图的遍历
深度优先遍历，简称DFS。
基本思想是从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。对于非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
对比两个不同存储结构的深度优先遍历算法，对于n个顶点e条边的图来说，邻接矩阵由于是二维数组，要查找每个顶点的邻接点需要访问矩阵中的所有元素，因此都需要O(n2)的时间。而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边的数量，所以是O(n+e)。
显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。
广度优先遍历，简称BFS。
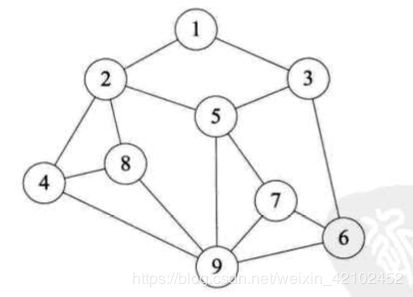
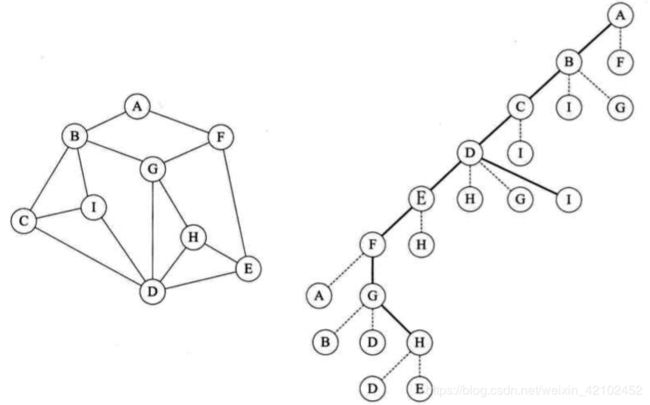
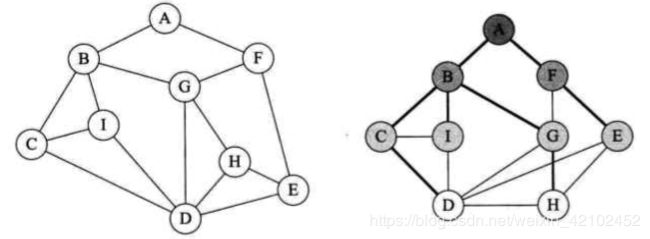
基本思想类似于树的层序遍历。我们将第一幅图稍微变形，变形原则是顶点A放置在最上第一层，让与它有边的顶点B、F为第二层，再让与B和F有边的顶点C、I、G、E为第三层，再将这四个顶点有边的D、H放在第四层，如第二幅图所示。此时在视觉上感觉图的形状发生了变化，其实顶点和边的关系还是完全相同的。
BFS与DFS的时间复杂度完全相同。
最小生成树
最小生成树即构造连通网的最小代价生成树。对比两个算法，克鲁斯卡尔算法主要是针对边来展开，边数少时效率会非常高，
所以对于稀疏图有很大的优势；而普里姆算法对于稠密图，即边数非常多的情况会更好一些。
Prim算法
Kruskal算法
最短路径
在网图和非网图中，最短路径的含义是不同的。
由于非网图它没有边上的权值，可看做是所有的边的权值都为1的网。所谓的最短路径，其实就是指两顶点之间经过的边数最少的路径。而对于网图来说，最短路径，是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。
Dijkstra算法（单源最短路径）
时间复杂度为O(n^2)。具体实现方式见例题。
Floyd算法（多源最短路径）
时间复杂度为O(n^3)。具体实现方式见例题。
拓扑排序
AOV网：在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系。AOV网中的弧表示活动之间存在的某种制约关系。即只有完成了某项活动，才能开始下一项。
设G=(V,E)是一个具有n个顶点的有向图，V中的顶点序列V1, V2, ..... Vn，满足若从顶点vi到vj有一条路径，则在顶点序列中顶点vi必在顶点vj之前。则我们称这样的顶点序列为一个拓扑序列。
所谓拓扑排序，其实就是对一个有向图构造拓扑序列的过程。构造时会有两个结果，如果此网的全部顶点都被输出，则说明它是不存在环的AOV网；如果输出顶点数少了，哪怕是少了一个，也说明这个网存在环，不是AOV网。
整个算法的时间复杂度为O(n+e)。
关键路径
AOE网：在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间。即针对有权值的网络的排序。
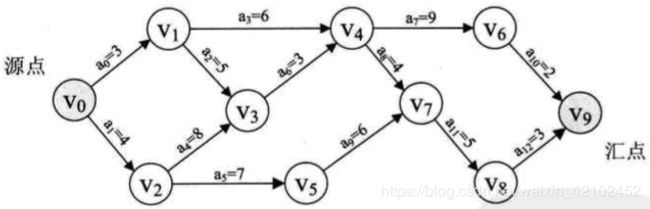
我们把AOE网中没有入边的顶点称为始点或源点，没有出边的顶点称为终点或汇点。由于一个工程，总有一个开始，一个结束，所以正常情况下，AOE网只有一个源点和一个汇点。Vo即是源点，表示一个工程的开始，V9是汇点，表示整个工程的结束，顶点 Vo, V1，..... V9分别表示事件，弧
我们把路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动叫关键活动。只有缩短关键路径上的关键活动时间才可以减少整个工期长度。
1、事件的最早发生时间 etv：即顶点Vk的最早发生时间。
2、事件的最晚发生时间 ltv：即顶点Vk的最晚发生时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个工期。
3、活动的最早开工时间 ete：即弧ak的最早发生时间。
4、活动的最晚开工时间 lte：即弧ak的最晚发生时间，也就是不推迟工期的最晚开工时间。
整个算法的时间复杂度为O(n+e)。
参考教材：
《数据结构与算法》，熊岳山著，清华大学出版社，2016，第二版
《2020年数据结构考研复习指导》，电子工业出版社，2020