python中的集合（包含栈的工作原理）

1.集合的创建

集合里面的元素是不可重复的

s = {1,2,3,1,2,3,4,5}
print(type(s))
print(s)

空集合的创建

s1 = set([])
print(type(s1))

集合的应用（去重）

li = [1,2,3,1,2,3]
print(list(set(li)))

2.集合的特性

集合没有索引、切片、连接、重复（如果强行使用，会出现TypeError报错），没有重复（如果强行使用，会出现TypeError报错）

1.for循环（迭代）

s = {1,2,3}
for i in s:
    print(i)

2.枚举

s = {1,2,3}
for i,v in enumerate(s):
    print('index: %s,value: %s' %(i,v))

3.成员操作符

s = {1,2,3}
print (1 in s)

3.集合的常用方法

集合：无序的数据类型
添加顺序和在集合中的存储顺序是不一样的

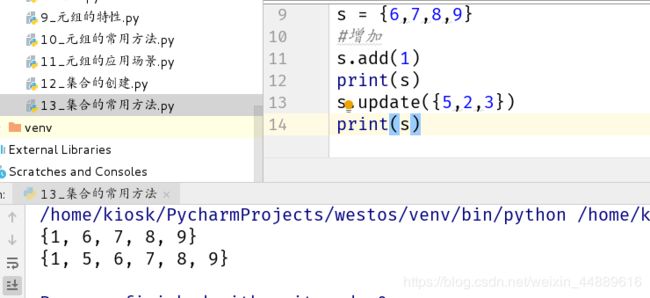
1.增加

s = {6,7,8,9}
s.add(1)
print(s)
s.update({5,2,3})
print(s)

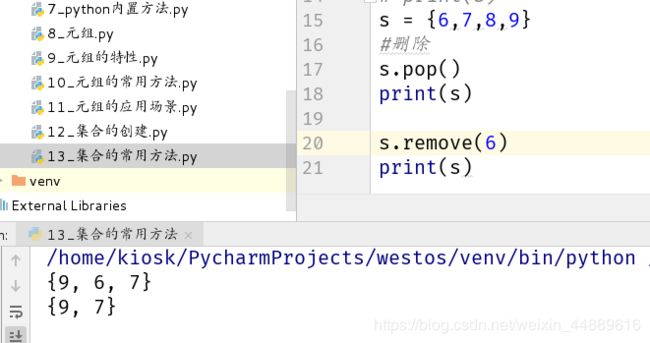
2.删除（pop是随机删除<可以在ipython中查看>，remove是删除指定的元素）

s = {6,7,8,9}
#删除
s.pop()
print(s)

s.remove(6)
print(s)

3.交集，并集，查集，对等差分

s1 = {1,2,3}
s2 = {2,3,4}
#并集
print('并集',s1.union(s2))
print('并集',s1|s2)
#交集
print('交集',s1.intersection(s2))
print('交集',s1&s2)
#差集
print('差集',s1.difference(s2))
print('差集',s2.difference(s1))
#对等差分：并集-交集
print('对等差分',s1.symmetric_difference(s2))
print('对等差分',s2.symmetric_difference(s1))

4.超集、子集是否相交

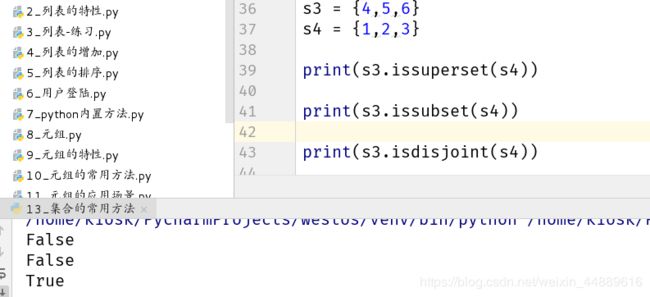
s3 = {4,5,6}
s4 = {1,2,3}
#判断s3是不是s4的超集/父集
print(s3.issuperset(s4))
#判断s3是不是s4的子集
print(s3.issubset(s4))
#两个集合是否不相交
print(s3.isdisjoint(s4))

练习：

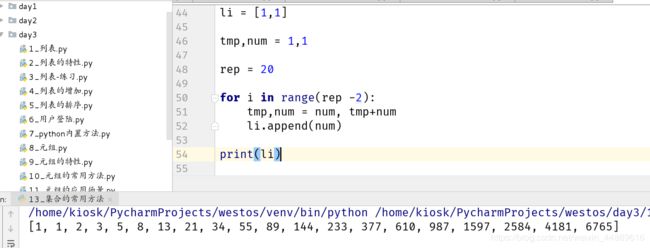
1.求前20个斐波那契数

li = [1,1]

tmp,num = 1,1

rep = 20

for i in range(rep -2):
    tmp,num = num, tmp+num
    li.append(num)

print(li)

2.去重
明明想在学校中请一些同学一起做一项问卷调查，为了实验的客观性
他先用计算机生成了N个1～1000之间的随机整数(N<=1000),N是用户输入的，对于
其中重复的数字，只保留一个，把其余相同的数字去掉，不同的数对应
着不同的学生的学号，然后再把这些
数从小到大排序，按照排好的顺序去找同学做调查，请你协助明明完成
“去重”与排序工作。

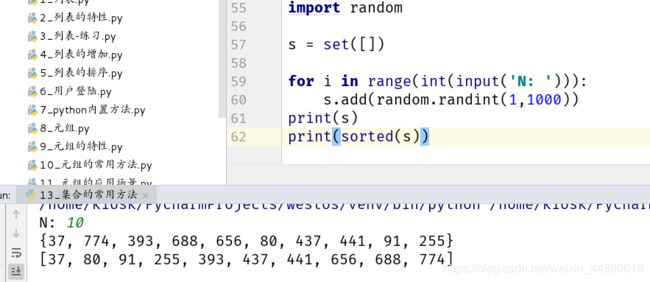
import random

s = set([])

for i in range(int(input('N: '))):
    s.add(random.randint(1,1000))
print(s)
print(sorted(s))

4.栈的练习

使用python程序模拟栈的工作原理：
　　入栈
　　出栈
　　查看栈顶元素
　　栈的长度
　　栈是否为空

stack=[]
print('栈操作目录'.center(50,'*'))
print("""
    1.入栈
    2.出栈
    3.查看栈顶元素
    4.栈的长度
    5.栈是否为空
    6.退出
""")
while True:
    choice = input('请输入选择：')
    ##1.入栈
    if choice == '1':
        a = input('输入添加的元素：')
        stack.append(a)
        print('元素%s添加成功' %a)
    ##2.出栈
    elif choice == '2':
        #先判断栈是否为空
        if not stack:
            print('栈为空，不能出栈')
        else:
            a=stack.pop()
            print('%s元素出栈成功' %a)
    ##3.查看栈顶元素
    elif choice == '3':
        if len(stack) == 0:
            print('栈为空')
        else:
            print('栈顶元素为%s' %(stack[-1]))
    ##4.查看栈的长度
    elif choice == '4':
        print('栈的长度为%s' %(len(stack)))
    ##5.栈是否为空
    elif choice == '5':
        if len(stack) == 0:
            print('栈为空')
        else:
            print('栈不为空')
    elif choice == 'q':
        print('退出')
        break
    else:
        print('请输入正确的选择')