剖析强化学习 - 第七部分

作者：Massimiliano Patacchiola

到目前为止，我们已经通过查找表（或者矩阵）表示效用函数。这种方法有一个问题，当潜在的马尔可夫决策过程很大时，有太多的状态和动作存储在内存中。此外，在这种情况下，访问所有可能的状态是非常困难的，这意味着我们无法估计这些状态的效用值。关键问题是泛化：如何产生一个只有很小子集的大状态空间的良好近似。在这篇文章中，我将向您展示如何使用特性的线性组合以便近似效用函数，这项新技术将使我们能够更有效地解决新老问题。例如，在本文中，您将学习如何实现TD(0)算法的线性版本以及如何使用它来查找多个gridworld的效用。

这篇文章的参考文献是Sutton和Barto所著的“泛化和函数逼近” 一书的第8章。另外一个很好的资源是David Silver的视频课程6。任何好的机器学习教科书都会给出函数逼近的更广泛的介绍，我建议阅读Christopher Bishop的模式识别和机器学习。我想通过神经科学领域短暂的旅行开始这篇文章，让我们看看函数逼近器如何与生物大脑相关。

Approximators（逼近器和祖母细胞）

如果不使用强大的逼近器：大脑，你无法阅读这篇文章。第一个原始大脑，一群神经细胞，给了基本生物更好的感知和反应，极大地延长了他们的寿命。千百年来，进化塑造了大脑，优化了容量、模块化和连接性。有一个大脑似乎至关重要，为什么？大脑的目的是什么？我们可以认为世界是一个巨大而混乱的状态空间，在这个空间中，对特定刺激的正确评估会导致生与死之间的差异，大脑存储有关环境的信息并允许与其进行有效的交互。假设我们的大脑是一个巨大的查找表，它可以存储单个状态在单个神经元（或单元）中，这被称为本地表示(local representation)，这个理论通常被称为祖母细胞(grandmother cell)。祖母细胞是一个假想的神经元，只对特定的和有意义的刺激作出反应，比如祖母的形象。这个术语是由认知科学家JerryLettvin提出的，他用它来澄清麻省理工学院讲座期间概念的不一致性。为了描述祖母细胞理论，我将使用下面的例子。假设我们带一个受试者到一个孤立的房间里，不断监测受试者大脑中一组神经元的活动。在受试者前面有一个屏幕，向他展示他的祖母的照片，我们注意到一个特定的神经元被激活，在不同的环境下展示祖母（例如在一组图片中）再次激活神经元，然而在屏幕上显示中性刺激不会激活神经元。

在20世纪70年代，祖母细胞进入神经科学期刊，并开始引起了适当的科学讨论。在同一时期，Gross等人（1972）观察到猴子的颞下皮层中的神经元选择性地对手和面部激活，祖母细胞理论开始被认真研究。这个理论很吸引人，因为它简单易懂，非常直观。然而，对祖母细胞的理论分析证实了许多潜在的弱点，例如，在这个框架中，一个细胞的损失意味着损失了一个特定的信息块，基本的神经生物学观察完全给出了相反的证据。有可能假设存在多个祖母细胞，它们以分布式的方式编码相同的信息，冗余的存在防止信息的损失。这种解释使情况更加复杂，因为存储单个状态需要查找表中有多个条目，存储N个状态为避免信息损失的风险，至少需要2 × N个细胞。祖母细胞的悖论是试图简化大脑的功能，最终使其复杂化。

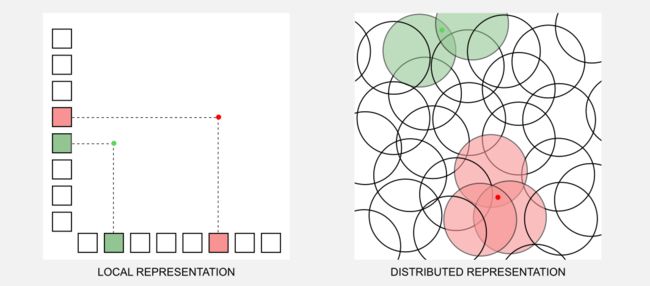
祖母细胞假说有其他方式吗？我们可以假设信息以分布式的方式存储，并且每个单一的概念通过一种活动模式来表示。Geoffrey Hinton（深度学习的“教父”之一）和James McClelland等研究人员强烈支持这一理论。分布式表示(distributed representation)理论给出的一大优势，有N细胞可能表示超过N个状态，而对于本地表示来说则不然。此外，分布式表示是鲁棒的，它防止了损失，保证了隐含的冗余。虽然每个活动单元的含义不那么具体，但活动单元的组合更具体。要理解这两种表示之间的区别，请参考计算机键盘，在本地表示中，每个单一的键只能编码一个字符，在分布式表示中，我们可以使用组合键（例如Shift和Ctrl）将多个字符关联到同一个键。在下面的图片中（灵感来自Hinton，1984）代表了两个刺激（红色和绿色的点）是如何在本地和分布式方案中编码的，本地方案被表示为一个二维网格，其中总是必须由两个活动单元来编码刺激。我们可以将分布式表示看作径向单元之间的重叠，两个刺激通过封闭在特定激活半径内的单元给出的高级模式进行编码。

使用分布式表示如何解释Gross等人（1972）描述的猴子选择性神经元？选择性神经元可以是封装信息的底层网络的可见部分。进一步的研究表明，这些选择性神经元在其反应性方面有很大的变化，并且它与面部的不同方面有关。这一观察结果表明，这些神经元嵌入了脸部的分布式表示。

如果你认为祖母细胞理论是七十年代出生和死亡的东西，那么你错了。近年来，本地表示理论得到了生物学观察的支持（参见Bowers 2009），然而这些结果受到了Plaut和McClelland（2009）的强烈批评。对于最近的一项调查，我建议你阅读这篇文章。从机器学习的角度来看，我们知道分布式表示的工作原理，深度学习的成功基于神经网络，它是强大的函数逼近器。另外，不同的方法，如dropout，与分布式表示理论密切相关。现在是回到强化学习的时候了，看看分布式表示如何解决由于本地表示造成的问题。

函数逼近的直觉

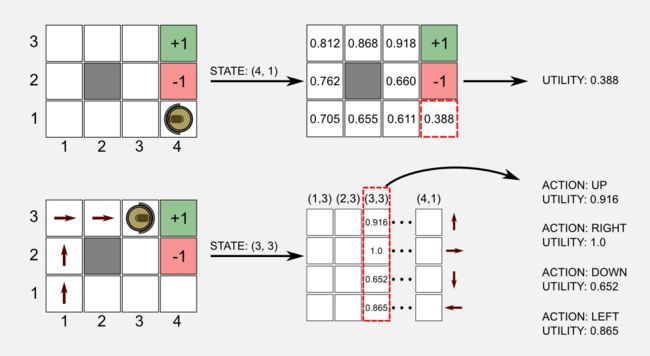
在这里我将再次使用之前文章中描述的清洁机器人示例。机器人在我们称之为gridworld的二维世界中移动，它只有4种可能的动作可用（前进、后退、左、右），其目标是到达充电器（绿色电池）并避免落在楼梯（红色电池）上。我用U(s)定义通常的效用函数，以及Q(s,a)定义状态-行动函数。网格世界是一个离散的矩形状态空间，具有c列和r行。使用表格方法，我们可以使用包含r × c = N个元素的表格表示U(s)，其中N代表状态的总数。为了表示Q(s,a)，我们需要一个大小为N × M的表格，其中M是动作的总数。在以前的文章中，我总是用矩阵表示查找表，作为效用函数，我使用了和世界具有相同大小的矩阵，而对于状态-动作函数，我使用了具有N列（状态）和M行（动作）的矩阵。在第一种情况下，为了获得效用，我们必须访问与我们所处的特定状态相对应的矩阵的位置；在第二种情况下，我们使用状态作为索引来访问状态-动作矩阵中的列，并从该列返回所有可用动作的效用。

我们如何在这个方案内拟合函数逼近机制？我们从一些定义开始，定义S={s1,s2,...,sN}为一组可能的状态， A={a1,a2,...,sM}为一组可能的动作，定义一个效用函数逼近器Û(S,w)，其参数存储在向量w中。在这里我使用带有上面帽子的Û函数来和表格版本U进行区分。

在解释如何创建函数逼近器之前，将其可视化为黑盒子很有帮助。下面介绍的方法可以用于不同的逼近器，因此我们可以很容易地将它应用于盒子内容。黑盒子将当前状态作为输入，并返回状态的效用或状态-动作的效用，主要优点是相对于表格方法，我们可以使用较少的参数逼近（具有任意小误差）效用。我们可以说存储在向量w中的元素的数量小于表格对应的值的数量N。

我猜你的脑中会有个问题：黑盒子里面有什么？这是一个合情合理的问题，现在我会尽力给你直觉的解释。在这种情况下黑盒子就是逼近一个效用函数，盒子的内容是Û (s,w)。您可以将效用函数想象为音乐混合器，权重的向量w作为混合器的滑块，我们想要调整滑块以获得与预定义音调相似的声音，怎么做？我们可以移动其中一个滑块并将输出与参考音调进行比较，如果输出与参考更类似，我们知道我们正确地移动了滑块。多次重复这个过程，我们最终获得与参考声音非常相似的音调。使用更正式的观点，我们可以说矢量w在每次迭代中调整，移动一个Δ量的值，以达到最小化成本函数的目标。成本由一个误差度量给出，我们可以将这个函数的输出与一个目标进行比较。例如，我们从以前的帖子就知道，我们在gridworld中的状态（4,1）的实际效用值是0.388。假设在时间t该盒子的输出是0.352，在更新步骤之后的输出是0.371，我们移动的结果更接近了目标值。

函数逼近是监督学习的一个实例。原则上，所有监督学习技术都可以用于函数逼近。矢量w可以是神经网络的连接权值或决策树的分裂点和叶子值的集合。然而在这里，我将只考虑可微函数逼近器，如特征和神经网络的线性组合，它代表了当今最有前途的技术。在这篇文章中，我将重点介绍特性的线性组合。

在描述线性逼近器的最简单情况之前，我想介绍用于调整权值向量的一般方法。函数逼近的目标是通过调整存储在w中的内部参数使其尽可能接近实际效用函数。为了实现这个目标，我们需要两件事情，第一是误差度量，它可以给我们一个关于我们与目标有多接近的反馈，第二是调整权重的更新规则。在下一节中，我将描述这两个组件。

方法

为了提高函数逼近器的性能，我们需要一个误差度量和一个更新规则，这两个组件在每个监督式学习技术的学习周期中都紧密合作，他们在强化学习中的使用与他们在分类任务中的使用方式没有多大区别。为了理解本节，您需要了解多变量微积分的一些概念，例如偏导数和梯度。

误差度量：常见误差度量由两个量之间的均方误差（MSE）给出。例如，如果我们有最优效用函数U∗(S)和一个逼近函数Û (s,w)，那么MSE定义如下：

就是这样，MSE是由期望E[(U∗ (s)− Û(s,w))2]给出，表示期望量化目标与逼近器输出之间的差异。当训练正常运行时，MSE会降低意味着我们越来越接近最优效用函数。MSE是监督学习中常用的损失函数，然而，在强化学习中，经常使用称为均方值误差（MSVE）的MSE的重新定义。所述MSVE引入一个分布μ(s)≥0，它规定了我们对每个状态s的关心程度。正如我告诉你的，函数逼近器是基于一组包含的元素数量少于状态总数的权重w，由于这个原因，调整权重的一个子集意味着提高某些状态的效用预测，但是会降低其它状态的精度。我们资源有限，必须认真管理它们，函数μ(s)给了我们一个明确的解决方案并使用它，我们可以重写以前的方程如下：

更新规则：可微逼近器的更新规则是梯度下降(gradient descent)。梯度是施加到多变量的标量值函数的导数概念的推广。您可以将梯度想象为指向最大增长率方向的矢量，直观地说，如果你想要到达山顶，那么梯度就是一个路标，在每个时刻都会显示你应该走向哪个方向。梯度通常用操作符∇表示，也被称为nabla。梯度下降的目标是最小化误差度量。我们可以实现向负梯度向量方向移动的目标，这意味着我们不再移动到山顶，而是向下移动，在每一步我们调整参数向量w向谷底靠近一步。首先，我们必须估计MSE(w)或MSVE(w)的梯度向量，这些误差函数基于w，为了得到梯度向量，我们必须计算每个权重相对于所有其他权重的偏导数。其次，一旦我们有梯度向量，我们必须根据梯度的负方向调整所有权重的值。用数学术语来说，我们可以在t+1时刻更新向量w如下：

最后一步应用了链式规则(chain rule)，因为我们正在处理一个函数组合。我们希望找到关于权重的误差函数的梯度向量，并且权重是我们的函数逼近器Û(s,wt)的一部分。数量1/2前面的减号用于改变梯度向量的方向，请记住，梯度指向山顶，而我们想要到底部（最小化误差）。最后，上面的规则告诉我们，我们需要的是逼近器的输出和它的梯度。寻找线性逼近器的梯度特别容易，而在非线性逼近器（例如神经网络）中，它需要更多的步骤。

在这一点上，你可能会认为我们有开始学习过程所需要的一切，然而还缺少一个重要的部分，我们认为使用最优效用函数U∗作为误差估计步骤中的目标是有可能的。我们没有最佳的效用函数，想想看，拥有这个函数意味着我们根本不需要逼近器。来到我们的网格世界中，我们可以简单地在每个时间步骤t调用U∗(st)并获得该状态的实际效用值。我们可以建立一个目标函数U∼来解决这个问题，它代表一个近似的目标并将其应用到我们的公式中：

如何估计近似目标？我们可以采用不同的方法，例如使用Monte Carlo或TD学习。在下一节中，我将介绍这些方法。

目标估计

在上一节中我们得出结论，我们需要近似目标函数U∼(s)和Q∼(s,a)用于误差评估和更新规则，所使用的目标类型是强化学习中函数逼近的核心。有两种主要方法：

蒙特卡洛目标(Monte Carlo target)：通过与环境的直接交互可以获得目标的近似值。使用蒙特卡洛方法（见第二篇文章），我们可以生成一个episode，并基于过程中遇到的状态更新函数U∼(s)。因为E[U∼(s)]= U∗ (s)所以最优函数U∗(s)的估计是无偏的，意味着预测保证收敛。

自助目标(Bootstrapping target)：用于构建目标的另一种方法称为自助，我在第三篇文章中介绍了它。在自助方法中，我们不必完成一个用于估计目标的episode，而是可以在每次访问后直接更新逼近器参数。自助目标的最简单形式是基于TD(0)的自助目标，其定义如下：

就是这样，目标是通过逼近器本身在st+1给出的近似值获得的。

我已经写了两种方法之间的区别，但是在这里我想在函数逼近的新环境中再次讨论它，在这两种情况下的函数U∼(s)和Q∼(s,a)基于权重w的向量，为此，我们打算从现在开始，使用正确的符号U∼(s,w)和Q∼(s,a,w)。在基于梯度的逼近器中使用自助法时，我们必须特别小心。自助法不是真正的梯度下降，因为它们只关心Û(s,w)中的参数。在训练时我们基于误差的度量调整在逼近器Û(s,w)中的w，但我们不改变基于误差度量的目标函数U∼(s,w)中的参数。自助法忽略了对目标的影响，仅考虑估计的梯度，由于这个原因，自助技术被称为半梯度法(semi-gradient methods)。由于这个问题，半梯度方法不能保证收敛。在这一点上，你可能会认为使用蒙特卡罗方法更好，因为至少它能保证收敛。自助法有两个主要优点。首先，它们能在线学习，并不需要完成episode来更新权重；其次，他们学习速度更快，并且计算更友好。

广义策略迭代（GPI）（见第二篇文章），在这里也适用。假设我们从一组随机权重开始，在第一步中，agent遵循ε-贪婪策略在最高效用的状态下移动，在第一步之后，可以使用梯度下降来更新权重。这种调整的效果是什么？效果是略微改善效用函数。在下一步，agent再次遵循贪婪策略，然后通过梯度下降更新权重，以此类推。正如你所看到的，我们再次应用了GPI方案。

线性逼近器(Linear approximator)

是时候把所有东西都放在一起了！我们已经建立了基于误差度量和更新规则的方法，并且我们知道如何估计目标。现在我将向您展示如何构建一个逼近器，由函数Û(s,w)表示的黑盒的内容。我将描述一个线性逼近器，它是线性组合的最简单情况，而在下一节中，我将描述一些高阶逼近器。在描述线性逼近器之前，我想澄清一个关键点以避免常见的误解，线性逼近器是更广泛的特征的线性组合的特例。线性组合基于多项式，它可以是或不是一条直线，仅使用一条直线来区分状态可能非常有限。线性组合意味着参数是线性组合的。我们没有提到任何有关输入特征的信息，事实上这些输入特征可能由高阶多项式表示。希望这个区别在帖子结尾会很清楚。

在线性逼近器中，我们将状态建模为向量x。该向量包含时间t的当前状态值，这些值被称为特征。向量x有不同的符号表示，但最常见的是x(st)和xt，我将使用这两个符号。这些特征可以是机器人的位置，倒立摆的角度位置和速度，围棋游戏中的棋子布局等。这里我还定义了w作为我们的线性逼近器的权重（或参数）的向量，它和x的元素数量相同。现在我们有两个向量，我们希望在线性函数中使用它们。怎么做？很简单，我们必须象下面这样在x和w之间执行点积：

如果你不习惯线性代数符号，不要害怕，这相当于以下的总和：

其中N是特性的总数。在几何上，这个解决方案由一条线（在二维空间中），一个平面（在三维空间中）或超平面（在超空间中）表示。现在我们知道黑盒的内容，它由向量x和w的乘积给出。然而，为了应用上一节中描述的方法，我们仍然需要误差度量、更新规则和目标。使用MSE，我们可以按如下方式定义误差度量：

使用TD(0)定义，我们可以如下定义目标：

之前定义的更新规则也可以在这里重用，但是我们必须引入奖励rt+1以及强化学习定义所要求的折扣因子gamma：

很好，我们几乎有了我们所需要的一切。我几乎忘了说明最后一点，更新规则需要梯度∇wÛ(s,w)。如何找到它？事实证明，线性逼近器的梯度简化为非常好的形式。首先，根据以前的定义，我们可以按如下方式重新定义梯度：

现在我们必须找到函数逼近器关于每个单个权重w1、w2、...的偏导数…。对于每个未知数，我们必须找到将其他未知数视为常数的导数，例如，第一个未知w1的偏导数是简单的x1，因为所有其他值都被认为是常数值，常数的导数为零：

对所有其他权重应用相同的过程，我们会得到以下梯度向量：

仅此而已，梯度是输入向量x(s)。现在我们可以重写更新规则如下：

太好了，这是线性逼近器更新规则的最终形式。我们拥有我们现在需要的一切。让我们开始派对吧！

应用：gridworld（偏置项）

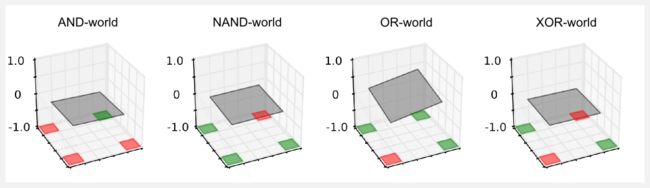
假设我们有一个方形网格世界，充电站（绿色单元）和楼梯（红色单元）分布在多个地点。正值和负值单元的位置可能会有所不同，从而产生四个世界我称之为OR-world、AND-world、NAND-world、XOR-world。世界的规则与前一篇文章中定义的相似，机器人有四个可用的动作：前进、后退、左、右，当执行动作时，有0.2的概率可能会导致错误的移动。绿色单元的奖励为正值（+1.0），红色单元为负值（-1.0），所有其他情况下无奖励值。状态的索引约定是通常的（列，行），其中（0,0）表示左下角的单元，（4,4）表示右上角的单元。

如果您熟悉布尔代数，您已经注意到世界中存在反映基本布尔运算的模式。从几何角度来看，当我们将线性逼近器应用于布尔世界时，我们试图在三维空间中找到一个平面，该平面可以区分具有高效用（绿色单元）和低效用状态（红色单元）。

在三维空间中，x轴由世界的列表示，而y轴由行表示，效用值由给定z轴给出。在梯度下降期间，我们不断改变权重，调整平面的倾斜度以及与每个状态相关的效用。为了更好地理解这一点，你在Wolfram Alpha中带入方程z=x+y，并查看结果图。更改与x和y关联的系数，会更改与这些特征相关的权重，而您实际上正在移动平面。用再试一次，或者如果你懒惰，请点击这里。

Python实现是基于自由在世界中移动的随机agent。在这里，我们只对估算状态效用感兴趣，我们不想找到一个策略。代码的核心是上一节中定义的更新规则，这要归功于Numpy，几行代码就可以搞定：

 

def update(w, x, x_t1, reward, alpha, gamma, done):
  '''Return the updated weights vector w_t1

  @param w the weights vector before the update
  @param x the feauture vector obsrved at t
  @param x_t1 the feauture vector observed at t+1
  @param reward the reward observed after the action
  @param alpha the ste size (learning rate)
  @param gamma the discount factor
  @param done boolean True if the state is terminal
  @return w_t1 the weights vector at t+1
  '''
  if done:
    w_t1 = w + alpha * (reward - np.dot(x,w)) * x)
  else:
    w_t1 = w + alpha * ((reward + (gamma*(np.dot(x_t1,w))) - np.dot(x,w)) * x)
  return w_t1

函数numpy.dot()是点积的实现，条件语句用于区分终止（done=True）和非终止（done=False）状态。在终止状态的情况下，只使用奖励获得目标，这是显而易见的，因为在终止状态之后，没有另一个状态用于近似目标。你可以在系列的官方GitHub仓库中查看完整的代码，python脚本名称为boolean_worlds_linear_td.py。在我的实验中，我设置了学习率α = 0.001，我线性地减少它到10– 6，运行3 × 104次迭代，权重随机地在[ - 1 ，+ 1 ]范围内初始化。使用matplotlib我在三维图中绘制为世界生成的平面：

平面的表面是线性逼近器返回的效用值，效用在红色单元附近应该为-1，在绿色单元附近为+1。然而，检查图我们注意到一些奇怪的事情发生了，除了OR-world，其它世界的平面是水平的，所得到的效用总是接近零。似乎逼近器根本不工作，并且其输出始终为空。到底怎么回事？我们目前对逼近器的定义没有考虑到一个重要因素，即平面平移。在xy平面上我们只有两个权重用于旋转表面，但是我们无法上下平移它。如果您考虑gridworld的单元(0,0)，这个问题会变得很清楚。这个单元的输入向量是x={0,0}，给定这个输入，不管我们为权重选择哪个值，当我们执行点乘积xTw时我们将最终得到零的效用。从几何的角度来看，平面可以旋转，但它被限制穿过点(0,0)。例如，在AND-world中，(0,0)中的约束特别令人不安，(4,4)中的效用无法调整到1.0，因为(0,4) 和(4,0)中的其他两个红色单元会出现更高的误差，最好的办法是保持平面水平，类似的推理可以应用于其它世界。只有在OR-world中，才有可能调整倾斜度并满足所有约束条件。我们如何解决这个问题？我们必须介绍偏置单元(bias unit)。偏置单元可以表示为总是等于1的附加输入。使用偏置单元，输入矢量变为x={x1,x2,...,xN,xb}，其中xb = 1。同时，我们必须在权向量w={w1,w2,...,wN,wb}中增加一个附加值，附加权重wb与其他权重类似地更新。再次使用Wolfram Alpha，您可以看到在我们通常的方程z = x + y + 1中插入偏置的效果是什么，以及关于具有零偏置的相同方程z = x + y的差异。我再次运行boolean_worlds_linear_td.py脚本，设置变量use_bias=True并使用与以前相同的超参数，获取以下图形：

结果好多了！平面不再水平，因为引入了偏置项，这样才有可能上下移动。现在可以调整平面以适应所有的限制，该脚本还将打印由该逼近器返回的权重向量和效用：

 

------AND-world------
w: [ 0.12578254  0.12194905 -0.71257655]
[[-0.21 -0.09  0.03  0.16  0.28]
 [-0.34 -0.21 -0.09  0.03  0.15]
 [-0.46 -0.34 -0.22 -0.1   0.03]
 [-0.59 -0.46 -0.34 -0.22 -0.1 ]
 [-0.71 -0.59 -0.47 -0.35 -0.22]]

------NAND-world------
w: [-0.12242233 -0.12346582  0.71111163]
[[ 0.22  0.1  -0.03 -0.15 -0.27]
 [ 0.34  0.22  0.1  -0.03 -0.15]
 [ 0.47  0.34  0.22  0.1  -0.03]
 [ 0.59  0.47  0.34  0.22  0.09]
 [ 0.71  0.59  0.46  0.34  0.22]]

------OR-world------
w: [ 0.12406486  0.11832163 -0.26037356]
[[ 0.24  0.35  0.47  0.59  0.71]
 [ 0.11  0.23  0.35  0.47  0.59]
 [-0.01  0.11  0.22  0.34  0.46]
 [-0.14 -0.02  0.1   0.22  0.34]
 [-0.26 -0.14 -0.02  0.09  0.21]]

------XOR-world------
w: [ 0.00220366 -0.00094763  0.00044972]
[[ 0.01  0.01  0.01  0.01  0.01]
 [ 0.01  0.01  0.01  0.    0.  ]
 [ 0.    0.    0.    0.    0.  ]
 [ 0.    0.    0.   -0.   -0.  ]
 [ 0.   -0.   -0.   -0.   -0.  ]]

在终端上打印的效用矩阵可以计算gridworld每个状态的线性逼近器的输出。在Numpy中，状态(0,0)是左上角的元素，打印矩阵时很难阅读，出于这个原因，矩阵已经被垂直翻转以便将值与gridworld的单元匹配。从效用值我们可以看到，在大多数的世界里，它们都非常好。例如，在AND-world中，我们应该有一个-1.0的状态(0,0)，逼近器返回-0.71的效用（矩阵中的左下角元素）。在另外两个红色单元中，值是-0.21和-0.22，它们并不如此接近-1.0，但至少是负值。状态（4,4）中的正单元具有1.0的效用，逼近器返回0.28。

在这一点上，应该清楚为什么使用函数逼近器是至关重要的。通过查找表方法，我们可以使用5行5列的表来表示布尔世界的效用，总共有25个变量保存在内存中。现在我们只需要两个权重和一个偏置，总共有3个变量。一切似乎都很好，我们有一个逼近器，它工作得很好，很容易调整。但是我们的问题还没有完成，如果你看看XOR-world，你会发现平面仍然是水平的。这个问题比前一个严重得多，并且没有办法解决它。在XOR-world中没有可以分隔红色和绿色单元的平面。尝试一下，调整平面以满足所有的限制条件，其结果是不可行的。该XOR-world 不是线性可分的，使用线性逼近器我们只能近似线性可分的函数。我们为XOR-world逼近效用函数的唯一机会是真正地去弯曲平面，要做到这一点，我们必须使用更高阶的逼近器。

高阶逼近器

线性逼近器是最简单的逼近方式。线性方式吸引人的地方，不仅因为它简单，而且因为它保证了收敛。但是，线性模型中存在一个重要的限制：它不能表示特征之间的复杂关系。就是这样，线性方式不允许表示特征之间的交互，这种复杂的交互自然会出现在物理系统中。有些特征只有在没有其它特征时才可以提供信息。例如，倒立摆角位置和速度紧密联系，高角速度是好的还是坏的取决于杆的位置。如果角度高，那么高角速度意味着即将发生坠落的危险，而如果角度低，那么高角速度意味着杆正在自我调整。

解决异或问题非常简单，只需附加特性。

如果你看看方程，我添加的是新的项x1x2w3，这个项引出了两个特征x1和x2之间的关系。现在，由方程表示的表面不再是一个平面，而是一个双曲抛物面，一个完全适应XOR-world的鞍形曲面。我们不需要重写更新函数，因为它保持不变。我们总是有一个特征的线性组合，并且梯度总是等于输入向量。在存储库中，您会找到另一个脚本xor_paraboloid.py，其中包含新逼近器的实现。运行与线性情况下使用的参数相同的脚本，我们会得到下图：

这里抛物面是用四种不同的视角表示的。训练结束时获得的结果表明效用值非常好。

 

w: [ 0.36834857  0.36628493 -0.18575494 -0.73988694]
[[ 0.73  0.36 -0.02 -0.4  -0.77]
 [ 0.37  0.17 -0.02 -0.21 -0.4 ]
 [-0.   -0.01 -0.01 -0.02 -0.02]
 [-0.37 -0.19 -0.01  0.17  0.35]
 [-0.74 -0.37 -0.01  0.36  0.73]]

我们应该在左下角和右上角有-1，逼近器返回-0.74和-0.77，这一结果是很好的估计。针对正状态类似的结果已经在左上角和右下角处得到，其中近似值返回0.73和0.77，这非常接近1.0的真实效用。我建议您使用不同的超参数（例如学习率alpha）来运行脚本，以查看最终绘图和效用表上的效果。

几何上的直觉是有帮助的，因为它给出了不同逼近器的更直接的直觉。我们看到，使用附加特征和更复杂的函数可以更好地描述效用空间。高阶逼近者可能会发现特征之间有用的联系，而纯粹的线性逼近者则不可能。高阶逼近器的一个例子是二次逼近器，在二次逼近器中，我们使用二阶多项式来模拟效用函数。

选择正确的多项式并不容易。像线性算子这样的简单逼近器可能会错过特征与目标之间的相关关系，而高阶逼近器可能无法推广到新的不可见的状态，通过机器学习中已知的微妙折衷(偏差-方差折衷)来实现最佳平衡。

结论

在这篇文章中，我介绍了函数逼近，并且我们看到了如何基于误差度量、更新规则和目标构建方法论。这种方法非常灵活，我们将在未来的帖子中再次使用它。此外，我介绍了线性方法，这是最简单的逼近器，线性函数逼近受到限制，因为它无法捕获要素之间的重要关系。使用高阶多项式通常可以解决问题，但仍然是一种有限的方法，因为对特征之间的关系进行建模仍然存在着设计选择。在复杂的物理系统中，多个元素之间相互作用，很难找到可能描述这些关系的正确多项式。如何解决这个问题呢？我们可以使用非线性函数逼近器。在下一篇文章中，我将介绍神经网络，并向您展示如何在强化学习中使用它。

索引

1.  [第一篇]马尔科夫决策过程，贝尔曼方程，值迭代和策略迭代算法。

2.  [第二篇]蒙特卡罗概念，蒙特卡洛方法，预测与控制，广义策略迭代，Q函数。

3.  [第三篇]时间差分概念，动物学习，TD(0), TD(λ)和资格痕迹，SARSA，Q-learning。

4.  [第四篇] Actor-Critic方法背后的神经生物学，计算Actor-Critic方法，Actor-only和Critic-only方法。

5.  [第五篇]进化算法介绍，强化学习中的遗传算法，遗传算法的策略选择。

6.  [第六篇]强化学习应用，多臂老虎机，山地车，倒立摆，无人机着陆，难题。

7.  [第七篇]函数逼近概念，线性逼近器，应用，高阶逼近器。

8. [第八篇] 非线性函数逼近，感知器，多层感知器，应用，政策梯度。 

资源

·   The complete code for theReinforcement Learning Function Approximation is available on the dissecting-reinforcement-learningofficialrepository on GitHub.

·     Reinforcement learning:An introduction (Chapter 8 ‘Generalization and Function Approximation’) Sutton, R.S., & Barto, A. G. (1998). Cambridge: MIT press. [html]

参考

Bowers, J. S. (2009). On the biological plausibility ofgrandmother cells: implications for neural network theories in psychology andneuroscience. Psychological review, 116(1), 220.

Gross, C. G., Rocha-Miranda, C. E. D., & Bender, D. B.(1972). Visual properties of neurons in inferotemporal cortex of the Macaque.Journal of neurophysiology, 35(1), 96-111.

Gross, C. G. (2002). Genealogy of the “grandmother cell”. TheNeuroscientist, 8(5), 512-518.

Hinton, G. E. (1984). Distributed representations.

Plaut, D. C., & McClelland, J. L. (2010). Locating objectknowledge in the brain: Comment on Bowers’s (2009) attempt to revive thegrandmother cell hypothesis.