java中compareable和comparator的区别，比较器实现的原理！

一、实现Compare接口与Comparator接口的类，都是为了对象实例数组排序的方便，因为可以直接调用

java.util.Arrays.sort(对象数组名称),可以自定义排序规则。

排序实现的原理都是基于红黑二叉树原理实现的。

不同之处：

1 排序规则实现的方法不同

Comparable接口的方法：compareTo(Object o)

Comparator接口的方法：compare(T o1, To2)

2 类设计前后不同

​ Comparable接口用于在类的设计中使用；设计初期，就实现这个借口，指定排序方式。

Comparator接口用于类设计已经完成，还想排序（Arrays）。

二、Comparable接口的实例操作

Student类创建时实现Comparable接口，覆写compareTo（）方法，

成绩按从高到低排序，成绩相等按年龄从小到大排序。

package ch11.lei.ji;
/*实现Comparator接口的类可以方便的排序，
 * 覆写compareTo接口
 * java.util.Arrays.sort(对象类数组)，*/
class Student implements Comparable<Student> {    // 指定类型为Student
    private String name ;
    private int age ;
    private float score ;
    public Student(String name,int age,float score){
        this.name = name ;
        this.age = age ;
        this.score = score ;
    }
    public String toString(){
        return name + "\t\t" + this.age + "\t\t" + this.score ;
    }
    public int compareTo(Student stu){    // 覆写compareTo()方法，实现排序规则的应用
        if(this.score>stu.score){
            return -1 ;
        }else if(this.score<stu.score){
            return 1 ;
        }else{
            if(this.age>stu.age){
                return 1 ;
            }else if(this.age<stu.age){
                return -1 ;
            }else{
                return 0 ;
            }
        }    
    }
};
public class Comparable01{
    public static void main(String args[]){
        Student stu[] = {new Student("张三",20,90.0f),
            new Student("李四",22,90.0f),new Student("王五",20,99.0f),
            new Student("赵六",20,70.0f),new Student("孙七",22,100.0f)} ;
        java.util.Arrays.sort(stu) ;    // 进行排序操作
        for(int i=0;i<stu.length;i++){    // 循环输出数组中的内容
            System.out.println(stu[i]) ;
        }
    }
};

三、Comparator接口实例操作

Student01类原先没有比较器，类完成后构建一个比较器StudentComparator类

按年龄从大到小排序。

package ch11.lei.ji;
import java.util.* ;
 class Student01{    // 指定类型为Student
    private String name ;
    private int age ;
    public Student01(String name,int age){
        this.name = name ;
        this.age = age ;
    }
    public boolean equals(Object obj){    // 覆写equals方法
        if(this==obj){
            return true ;
        }
        if(!(obj instanceof Student)){
            return false ;
        }
        Student01 stu = (Student01) obj ;
        if(stu.name.equals(this.name)&&stu.age==this.age){
            return true ;
        }else{
            return false ;
        }
    }
    public void setName(String name){
        this.name = name ;
    }
    public void setAge(int age){
        this.age = age ;
    }
    public String getName(){
        return this.name ;
    }
    public int getAge(){
        return this.age ;
    }
    public String toString(){
        return name + "\t\t" + this.age  ;
    }
};

class StudentComparator implements Comparator<Student01>{    // 实现比较器
    // 因为Object类中本身已经有了equals()方法
    public int compare(Student01 s1,Student01 s2){
        if(s1.equals(s2)){
            return 0 ;
        }else if(s1.getAge()<s2.getAge()){    // 按年龄比较
            return 1 ;
        }else{
            return -1 ;
        }
    }
};

public class Comparator01{
    public static void main(String args[]){
        Student01 stu[] = {new Student01("张三",20),
            new Student01("李四",22),new Student01("王五",20),
            new Student01("赵六",20),new Student01("孙七",22)} ;
        java.util.Arrays.sort(stu,new StudentComparator()) ;    // 进行排序操作
        for(int i=0;i<stu.length;i++){    // 循环输出数组中的内容
            System.out.println(stu[i]) ;
        }
    }
};

四、当用到自定义排序器的时候

如：Collections.sort中需要传入一个自定义的排序器，使用匿名内部类的方式,传入comparator,重写方法，使用A.compareToB的方式进行排序

    static void sortByValue(Map map) {
        List<Map.Entry<String, Integer>> list = new ArrayList<Map.Entry<String, Integer>>(map.entrySet());
        Collections.sort(list, new Comparator<Map.Entry<String, Integer>>() {
            @Override
            public int compare(Map.Entry<String, Integer> o1, Map.Entry<String, Integer> o2) {
                return o1.getValue().compareTo(o2.getValue());
            }
        });
        for (Map.Entry<String, Integer> mapping : list) {
            System.out.println("键：" + mapping.getKey() + " 值：" + mapping.getValue());
        }

五、个人对红黑树设计思想的感想

如果不了解红-黑树的设计思想，死套相应的操作规则，是件很头疼的事情，知其然而不知其所以然，也是工程师的大忌。可惜，在网上找了不少资料，都介绍红-黑树的工作流程。在这里，我大胆地猜想一下红黑树的设计思想。

红-黑树的设计思想应该是，利用红-黑这两种节点颜色来追踪二叉树的平衡状况，重新着色(recolor)这个操作就是动态刷新各节点颜色，如果发现树开始出现不平衡状况，就使用左旋(leftrotate)或者右旋(rightrotate)来改变树的结构。

把图(tree 2) 和(tree 3) 反过来看，它们都是不平衡树，对(tree 2)进行右旋，或对(tree4)进行左旋都能得到(tree3)这样的平衡树。左旋的实质是增加左树的高度而减少右树的高度，右旋反之。这样交替运用这三个操作，我们就可以构建一颗平衡的二叉树。

插入

通过上面对设计思想的分析，插入的工作流程就非常简单了。

首先分析父亲节点和叔叔节点的颜色，判断“父亲”和“叔叔”的势力是否平衡。如果平衡，则直接插入，然后进行recolor 操作，继续最踪插入后的情况。否则把"爷爷这颗子树"(父亲节点，爷爷节点和叔叔节点）左(右)旋以后再插入。

如何判断"爷爷"这颗子树是否平衡呢？

这就是红-黑树的核心了，通过 "父亲"与"叔叔"的颜色来判断。如果他们同时为红色或者黑色，那么"爷爷"这颗子树是平衡的。否则，就不平衡。需要进行旋转操作来平衡

这两者的势力。

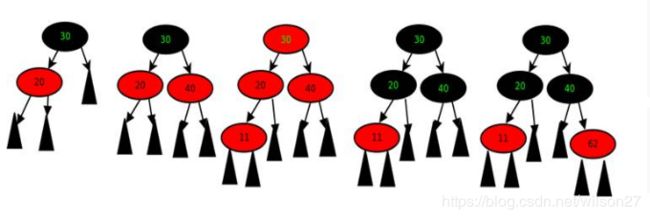
按照红-黑树的规则，根节点 30 必须是黑色，然后，我们插入 20，为了不违反各分支，黑节点数相等的原则，20必须是红色，接着再插入红色节点40，so good,so far. 现在插入节点11。

现在问题出来了，按照红节点必要有黑父亲的规则， 11 和 20 出现了冲突，这种情况下，需要进行 recolor 操作： 20 和 40 调整为黑色，同时把 11 的爷爷 30 调整为红色，这样可以保证 30 这颗子树的黑节点数目不变。

如果 30 的父亲节点恰好也是红色，需要执行插入红色节点 30，如果 30的父亲是黑节点，调整结束，如果30是根节点根据规则，把它改成黑节点，此时，各分支节黑点数+1变成了2，数目仍然相等。如果插入的数据是平衡的，我们只需要重复执行，上述操作，插入红节点，recolor。

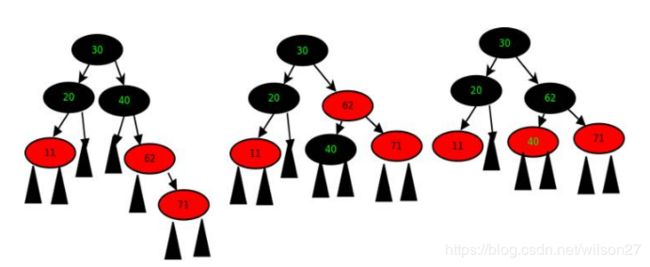
继续插入 71，发现 71的父亲 62 这个节点没有兄弟节点，很明显以71的爷爷40作为根节点子树，已经不平衡了，因为，平衡的情况应该是，62有一个红色的兄弟节点——这样的话，我们只需要递归执行recolor 即可。

可惜，62没有兄弟，于是，左旋一下(40-62-71) 这颗树，左旋以后，黑色根节点40变成了孩子节点，需要把的黑色上提，同新的根节点62交换颜色，以保证黑色节点数目不变。就这样交替执行下去，我们就会得到一颗平衡的二叉树。

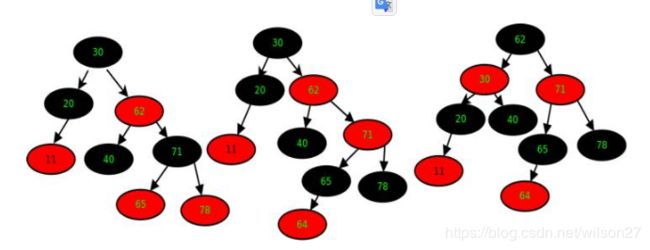
继续插入 65，recolor 40, 71, 62这三个节点。 OK，我们继续插入 78，64，当插入64需要 recolor 65, 78 71 三个节点。 recolor 以后， 71 与 62同为红色节点，违反了规则，此时，执行一个递归算法，把71当成一个新接点插入。

现在让我们来插入新节点 71，由于 62 与 20颜色不相同， 30为根节点的这颗树不平衡，需要左一个左旋的操作。

同时 62 与30 互换颜色。现在，71的父亲为根节点，递归结束，71 插入成功