数据结构与算法|第十章：排序-下

数据结构与算法|第十章：排序-下

前言

本章会讨论三种时间复杂度是 O(n) 的排序算法：桶排序、计数排序、基数排序。

因为这些排序算法的时间复杂度是线性的，所以我们把这类排序算法叫作线性排序（Linear sort）。之所以能做到线性的时间复杂度，主要原因是，这三个算法是非基于比较的排序算法，都不涉及元素之间的比较操作。

这几种排序算法理解起来都不难，时间、空间复杂度分析起来也很简单，但是对要排序的数据要求很苛刻，所以我们本章讨论的重点是掌握这些排序算法的适用场景。

1.项目环境

• jdk 1.8
• github 地址：https://github.com/huajiexiewenfeng/data-structure-algorithm
  • 本章模块：chapter07

2.桶排序(Bucket Sort)

2.1 原理图解

核心思想是将需要排序的数据分到几个桶中，每个桶再单独进行排序，在桶中排序完成之后，再将数据依次取出，最后组成序列就是有序的。

假设我们现在一个班级的 20 位同学考试数学分数（满分100分）进行排序，我们可以先根据 100 分来平均分为 5 个桶，再按照分数依次将分数放入对应桶中，对每个桶进行排序。

如果要排序的数据有 n 个，我们均匀的分配到 m 个桶中，每个桶有 k = n/m 个元素。如果每个桶内部排序使用快排，时间复杂度为 $O(k\ast logk)$，m 个桶时间复杂度为 $O(m\ast k\ast logk)$ , 因为 k = n/m，所以整个桶排序的时间复杂度 $T(n)=O(n\ast logk)$，当桶 m 的个数接近 n 的个数，$logk$ 的值是一个常量，这时候桶排序的时间复杂度接近 $O(n)$ 。

从上面的分析可以看出，桶排序的限制条件很多，对需要排序的数据有一定的要求比如

• 需要排序的数据可以比较容易的划分成 m 个桶
• 桶之前有大小的顺序
• 桶中分配的数据相对比较均匀，如果所有的人都考 81-100 分，那么桶排序的时间复杂度就退化为 $O(nlogn)$

2.2 代码实现

    /**
     * 桶排序
     *
     * @param numbers    需要排序的数组
     * @param bucketSize 桶容量
     */
    private static void bucketSort(int[] numbers, int bucketSize) {
        // 获取数组的最大值和最小值
        int maxValue = numbers[0];
        int minValue = numbers[0];
        for (int i = 0; i < numbers.length; i++) {
            if (numbers[i] > maxValue) {
                maxValue = numbers[i];
            }
            if (numbers[i] < minValue) {
                minValue = numbers[i];
            }
        }
        System.out.println("最大值：" + maxValue);
        System.out.println("最大值：" + minValue);
        // 计算桶的数量
        int bucketCount = (maxValue - minValue) / bucketSize + 1;
        // 创建桶
        int[][] buckets = new int[bucketCount][bucketSize];
        // 每个桶中的下标数组
        int[] indexArr = new int[bucketCount];

        // 将 numbers 数组中的元素均匀的分配到桶中
        for (int i = 0; i < numbers.length; i++) {
            int number = numbers[i];
            //计算桶的位置
            int bucketIndex = (number - minValue) / bucketSize;
            buckets[bucketIndex][indexArr[bucketIndex]++] = number;
        }
        int k = 0;
        // 每个桶进行排序，这里使用快排
        for (int i = 0; i < buckets.length; i++) {
            quickSort(buckets[i], 0, indexArr[i] - 1);
            // 最后将桶的数据依次插入到原数组中
            for (int j = 0; j < indexArr[i]; j++) {
                numbers[k++] = buckets[i][j];
            }
        }
    }

测试调用

    public static void main(String[] args) {
        // 随机生成1000长度的数组，数组元素10000以内
        int[] numbers = new int[1000];
        for (int i = 0; i < 1000; i++) {
            numbers[i] = new Random().nextInt(10000);
        }
        System.out.println("排序前:" + Arrays.toString(numbers));
        bucketSort(numbers, 100);
        System.out.println("排序后:" + Arrays.toString(numbers));
    }

执行结果：

2.3 排序分析

因为桶排序中应用到了快速排序，如果划分的 m 个桶，数据均匀分布，那么最好时间复杂度为 $O(n)$ ；如果所有的数据都在一个桶中，最坏时间复杂度 $O(nlogn)$ 。

3.计数排序(Counting Sort)

3.1 原理图解

假设需要排序的数组A 为 [2,5,0,3,5,0,3,5] 有 8 个元素。

这里元素的最大值为 5

我们新建一个 数组C 长度为 6，数组下标用来表示 数组A 的元素值，而数组本身的元素用来表示这个下标值出现的次数

这样计数的好处在于，我们可以通过合计元素的方式知道某一个元素在最后的有序数组中的数组下标位置在哪。

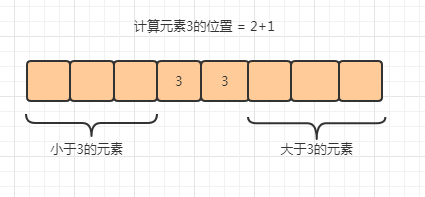
我们继续向下推进，一步一步让元素最终存储在对应的位置上

首先我们对前面的 数组C[6] 顺序求和

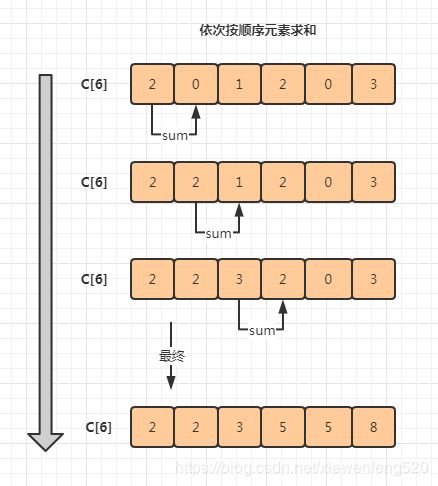
接下来我们可以开始进行最后的排序了，利用 C[6] 数组，将元素放到 R[8]数组正确位置中来完成排序。这个过程相当巧妙，需要一步一步跟着图解进行。

我们从后往前扫描原数组A [2,5,0,3,5,0,3,5] ，最后一个元素为 5，在 C[6] 中查找 5 的位置为8，将 5 插入到 数组R 7的下标位置，同时 C[6] 中下标为 5 的元素 8 - 1=7。然后从 原数组A 依次这样从后往前取元素进行上述过程

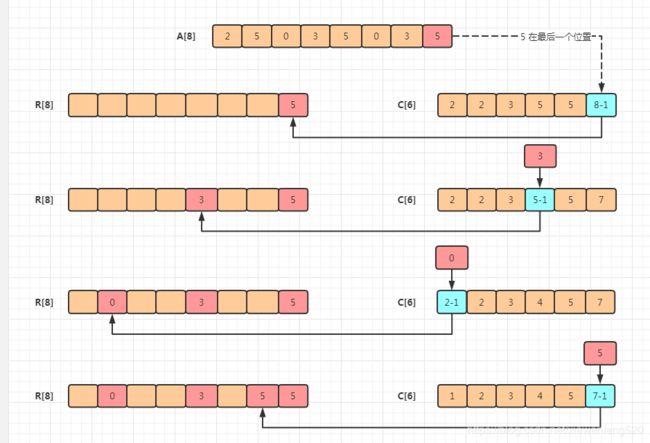
可以看到经过上面的步骤，所有的元素都存储到了正确的位置上完成了排序。

3.2 代码实现

private static int[] countingSort(int[] numbers) {
        int maxValue = numbers[0];

        // 查找数组的最大值
        for (int i = 0; i < numbers.length; i++) {
            if (maxValue < numbers[i]) {
                maxValue = numbers[i];
            }
        }

        // 计数数组
        int[] countArr = new int[maxValue + 1];

        // 统计每个元素出现的次数
        for (int i = 0; i < numbers.length; i++) {
            countArr[numbers[i]]++;
        }

        // countArr 顺序求和
        for (int i = 1; i < maxValue + 1; i++) {
            countArr[i] = countArr[i - 1] + countArr[i];
        }

        int[] resArr = new int[numbers.length];

        // 倒序插入
        for (int i = numbers.length - 1; i >= 0; i--) {
            // 获取最后一个元素
            int number = numbers[i];
            // 找到元素对应的 count 计数值
            int indexCount = countArr[number] - 1;
            // 插入到对应的结果数组中
            resArr[indexCount] = number;
            // 对应的 countArr 的 count -1
            countArr[number] = indexCount;
        }

        return resArr;
    }

测试代码

    public static void main(String[] args) {
        // 随机生成100长度的数组，数组元素100以内
        int[] numbers = new int[100];
        for (int i = 0; i < 100; i++) {
            numbers[i] = new Random().nextInt(100);
        }
        System.out.println("排序前:" + Arrays.toString(numbers));
        numbers = countingSort(numbers);
        System.out.println("排序后:" + Arrays.toString(numbers));
    }

执行结果：

3.3 排序分析

利用一个计数的数组来进行最后元素的排序的实现方式，所以这种排序叫做计数排序，可以看出计数排序是一种更加特殊的桶排序，桶的个数就是元素的最大值，每个桶中放着相关的元素，所以计数排序的使用场景限制条件更苛刻；一般数据范围如果比数据量大很多，就不适合计数排序，而且计数排序只能给非负整数排序。

比如某高校全体学生考试分数(人数5000>总分100)的排序，或者是整个集团的人员绩效考核分数的排序(人数20k+>总分100)，就可以使用计数排序。

对应负数的情况，解决方案是统一加上一个值，使其变为正数，比如数据范围是[-100,100]，统一加 100 即可。

对应小数的情况，解决方案是统一乘以10、100、1000 使得小数变为整数。

4.基数排序(Radix Sort)

4.1 原理图解

这里我们假设一个实际场景，比如我们现在需要对 10 万个手机号码进行排序，手机号长度为固定的 11 位。用桶和计数显然不太合适，因为最大值太大了，那么我们这里就可以使用基数排序。

比较两个手机号 A,B 的大小，其实只需要依次比较手机号的前几位，如果前几位 A 已经大于 B，其实后面就不需要比较了。

为了方便我们只模拟手机号的前面 4 位

第一次排序根据第 4 位

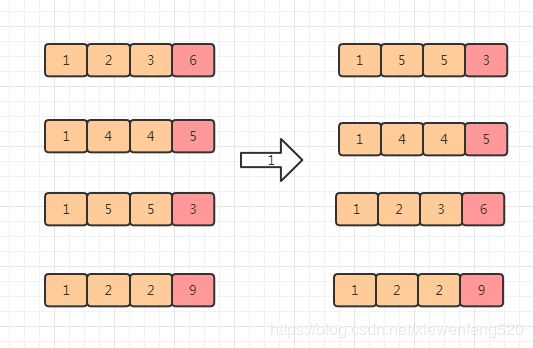
第二次排序更新 第 3 位

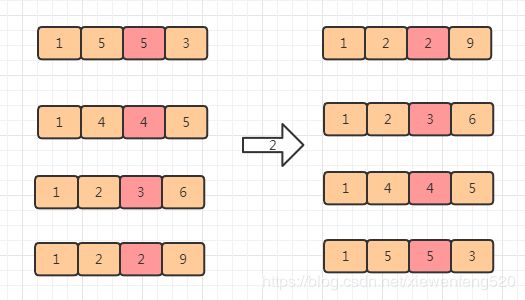
第三次排序以及第四次排序

由此可知，手机号的排序只需要经过 11 次这样的操作，就可以完成排序。

根据每一位来排序，我们可以使用前面的桶排序或者计数排序，他们的时间复杂度是 O(n)，如果要排序的数据有 k 位，那么基数排序的时间复杂为 $O(k\ast n)$，在这个手机号的例子中，k = 11 相对应数据量 10 万来说可以忽略，所以基数排序的时间复杂为 $O(n)$。

4.2 代码实现

    private static void radixSort(int[] numbers) {
        // 找到数组中的最大值
        int maxValue = numbers[0];

        // 查找数组的最大值
        for (int i = 0; i < numbers.length; i++) {
            if (maxValue < numbers[i]) {
                maxValue = numbers[i];
            }
        }

        // 根据位数分别进行计数排序
        for (int exp = 1; maxValue / exp > 0; exp *= 10) {
            numbers = countingSort(numbers, exp);
        }

        System.out.println("排序后:" + Arrays.toString(numbers));
    }

每一位的排序使用计数排序

    private static int[] countingSort(int[] numbers, int exp) {

        // 计数数组
        int[] countArr = new int[10];

        // 统计每个元素出现的次数
        for (int i = 0; i < numbers.length; i++) {
            countArr[(numbers[i] / exp) % 10]++;
        }

        // countArr 顺序求和
        for (int i = 1; i < 10; i++) {
            countArr[i] = countArr[i - 1] + countArr[i];
        }

        int[] resArr = new int[numbers.length];

        // 倒序插入
        for (int i = numbers.length - 1; i >= 0; i--) {
            // 获取最后一个元素
            int number = numbers[i];
            // 找到元素对应的 count 计数值
            int indexCount = countArr[(number / exp) % 10] - 1;
            // 插入到对应的结果数组中
            resArr[indexCount] = number;
            // 对应的 countArr 的 count -1
            countArr[(number / exp) % 10] = indexCount;
        }

        return resArr;
    }

测试代码

NumberUtil 工具类，在 github 源码中，这里就不贴出来了

    public static void main(String[] args) {
        // 随机生成100长度的数组，数组元素 9 位以内的数字，长度不够补 0
        int[] numbers = new int[10];
        for (int i = 0; i < 10; i++) {
            numbers[i] = NumberUtil.generateInt(9, "");
        }
        System.out.println("排序前:" + Arrays.toString(numbers));
        radixSort(numbers);
    }

执行结果：

排序前:[873821058, 458253267, 929618850, 901593128, 740762318, 931105657, 645886638, 137590327, 683633730, 329975231]
排序后:[137590327, 329975231, 458253267, 645886638, 683633730, 740762318, 873821058, 901593128, 929618850, 931105657]

4.3 排序分析

基数排序对数据也是有限制和要求的，被排序的数据必须可以分割出来 “位” 进行单独的比较。

5.小结

本章讨论了三种线性时间复杂度的排序算法，有桶排序、计数排序、基数排序。它们对要排序的数据都有比较苛刻的要求，应用不是非常广泛。但是如果数据特征比较符合这些排序算法的要求，应用这些算法，会非常高效，线性时间复杂度可以达到O(n)。

桶排序和计数排序的排序思想是非常相似的，都是针对范围不大的数据，将数据划分成不同的桶来实现排序。

基数排序要求数据可以划分成高低位，位之间有递进关系。比较两个数，我们只需要比较高位，高位相同的再比较低位。而且每一位的数据范围不能太大，因为基数排序算法需要借助桶排序或者计数排序来完成每一个位的排序工作。

6.参考

• 极客时间 -《数据结构与算法之美》王争