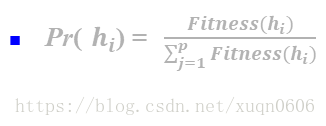数据挖掘笔记——遗传算法

      遗传算法来源于进化论，可以理解为一开始我们产生很多个随机解，构成第一代假设集合(也叫做种群)，由这些随机解产生一代新的种群并进行假设解集合的更新，在产生下一代随机解过程中，好的解保留，差的解遗弃，即通过变异和交叉迭代每一步。

    总结来说，遗传算法是在候选假设中找到最优假设的过程。

1.遗传算法结构

          (1)种群：在算法中迭代更新的假设集合

       （2）适应度函数：判断假设好坏的定量值

       （3）如何选出适应度较高的假设：一部分假设进行变异，一部分假设进行交叉操作。具体如何做后面详细讲。

   故模型为： GA（Fitness，Fitness_threshold,p,r,m）

          Fitness:适应度函数，输入为某函数输出为判断值

              Fitness_threshold:适应度阈值，即迭代停止条件

              p:种群中假设的个数；r:每一步进行交叉那一部分的比例；m:变异的比例

2.算法过程

    1. 初始化种群P：随机的产生p个假设

      2.评估：对P中的每一个假设h，计算该假设的适应度Fitness(h)

      3.当P中假设最大的适应度仍小于 Fitness_threshold重复迭代下面步骤，直到满足停止条件：

      产生新的一代种群Ps:

         (1)选择：从源种群P中选择p(1-r)个假设加入Ps中，每个假设的选择概率为

                           

          (2)交叉：还是依照pr(h)的概率从P中选择对假设，每一对假设通过交叉操作都产生两个后代

          (3)变异：在新种群Ps中均匀地选择m%个假设，表示该假设的比特串对其中一位进行求反

      4.更新：使用Ps代替P

      5.停止迭代后，返回适应度最大的假设

3.假设的表示

    假设使用比特串表示,如下例：

4.遗传算法

  4.1.交叉操作

         从两个父母串产生两个后代，后代的串通过交叉掩码确定复制父母串的位置，进而形成自己的表示串。如下图所示。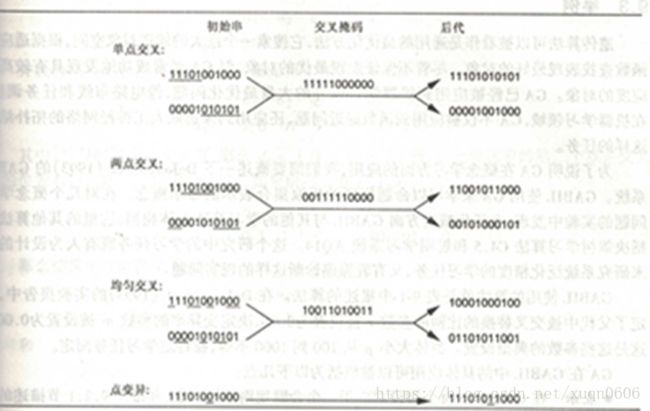

      拿第一个单点交叉来说，第一个后代前五位来自第一个父母串，后六位来自第二个父母串；第二个后代前五位来自第二个父母串，后六位来自第一个父母串。这里介绍一个后代生成规则——GABIL system

       每个假设对应一个命题规则的析取集。规则的假设空间由一组固定属性的约束组合构成。为了表示一组规则，将单个规则的位串表示连接起来。下图中a1和a2是两个布尔属性，c是分类。后代取复制的子串时定义两个index值，例如d1=1和d2=3。

如果第一个父母串划分已经确定，则第二个父母串可以是<1,3>均在前五位进行划分，<1,8>左边划在前五位右边划在后五位，<6,8>均在后五位划分。那么h3选择图中h1中括号外的部分和h2中括号内的部分。

4.2.变异操作

       对该假设串任取一位取反

4.3.适应度函数

       适应度函数可以通过一系列标注的数据进行训练得到，除了分类准确率，适应度还可以包括规则的复杂度和一般性。

5.总结

（1）不同于梯度下降每次只改进一点点，遗传算法可以产生于父代假设完全不同的子代假设，不易陷于局部最小。

（2）拥挤问题：由于适应度越高越有可能产生后代，因此多次迭代后，很有可能多个后代是同源的假设，这样就丧失了假设的多样性，搜索速度降低。

  解决方法：a.改变选择函数，不再依照适应度作为概率可以改为排名选择(任选两个取最大)

                   b.适应度共享，如果相似个体较多，则降低每个个体的适应度