实验三Huffman编解码算法实现与压缩效率分析
#实验目的
- 掌握Huffman编解码实现的数据结构和实现框架,进一步熟练掌握使用C编程语言,并完成压缩效率的分析。
- 本实验是一个主函数+库的方案,体会设计思想。
#实验内容 - Huffman算法:把每个字符看作一个单结点子数放在一个树集合中,每棵子树的权值等于相应字符的频率。每次取权值最小的两棵子树合并成一棵新树,并重新放到集合中,新树的权值等于两棵子树权值之和。
- Huffman编码程序思想:
(1) 将文件以ASCII字符流的形式读入,统计每个符号的发生频率
(2) 将所有文件中出现过的字符按照频率从小到大的顺序排列
(3) 每一次选出最小的两个值,作为二叉树的两个叶子节点,将和作为它们的根节点,这两个叶子节点不再参与比较,新的根节点参与比较
(4) 重复3,直到最后得到和为1的根节点
(5) 将形成的二叉树的左节点标0,右节点标1,把从最上面的根节点到最下面的叶子节点,途中遇到的0、1序列串起来,得到了各个字符的编码表示 - Huffman编码的数据结构设计:
在程序实现中使用二叉树的数据结构实现Huffman编码
(1) Huffman节点结构
(2) Huffman结构 - Huffman编解码实验流程
- getopt()函数分析:
#实验步骤
##调试程序
调试Huffman的编码程序,对照编码算法步骤对关键语句加上注释,并说明进行操作
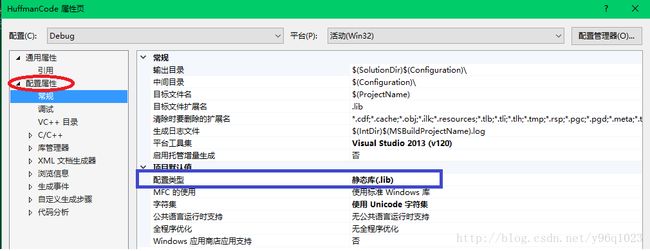
###本实验用到主函数+库的方案
整个工程文件由两个项目组成,第一个项目为 霍夫曼编码模块的具体实现->HuffmanCode,创建项目时选择的是静态库,生成一个 .lib 文件。第二个项目是主工程文件->HuffmanRun,我们运行此工程时只需要设置包含Huffmancode的库就可以调用其中的编码函数。HuffmanRun项目属性需要配置库目录和附加依赖性属性,库目录编辑添加HuffmanCode.lib 生成文件的路径。由于代码中用到了字节序转换的函数 htonl、ntohl,附加依赖项除添加HuffmanCode.lib 还需包含 ws2_32.lib。
##Huffman编码程序的整体框架如下图所示:
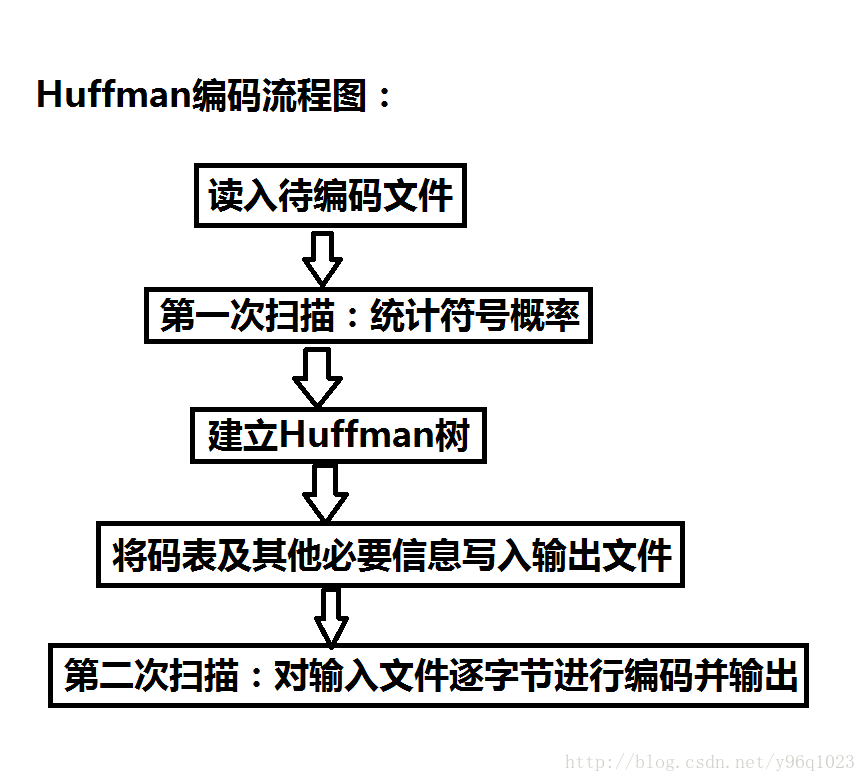
###对编码程序代码进行注释分析如下:
主函数main.c
int main(int argc, char** argv)
{
char memory = 0;//memory指示是否对内存数据进行操作
char compress = 1;//compress=1:编码 0:表示解码
int opt;
const char *file_in = NULL, *file_out = NULL;
//step1:add by yzhang for huffman statistics
const char *file_out_table = NULL;
//end by yzhang
FILE *in = stdin;
FILE *out = stdout;
//step1:add by yzhang for huffman statistics
FILE * outTable = NULL;
//end by yzhang
/* Get the command line arguments. */
while((opt = getopt(argc, argv, "i:o:cdhvmt:")) != -1)
//读取命令行参数的选项
{
switch(opt)
{
case 'i':
file_in = optarg;//输入文件
break;
case 'o':
file_out = optarg;//输出文件
break;
case 'c':
compress = 1;//压缩操作
break;
case 'd':
compress = 0;//解压缩操作
break;
case 'h':
usage(stdout);//输出参数用法说明
return 0;
case 'v':
version(stdout);//输出版本号信息
return 0;
case 'm':
memory = 1;//m对内存数据进行编码
break;
// by yzhang for huffman statistics
case 't':
file_out_table = optarg;
break;
//end by yzhang
default:
usage(stderr);
return 1;
}
}
/* If an input file is given then open it. */
if(file_in)//读取输入文件
{
fopen_s(&in,file_in, "rb");
if(!in)
{
fprintf(stderr,
"Can't open input file '%s': %s\n",
file_in, strerror(errno));
return 1;
}
}
/* If an output file is given then create it. */
if(file_out)//读取输出文件
{
fopen_s(&out,file_out, "wb");
if(!out)
{
fprintf(stderr,
"Can't open output file '%s': %s\n",
file_out, strerror(errno));
return 1;
}
}
//by yzhang for huffman statistics
if(file_out_table)//确认输出码表文件存在
{
fopen_s(&outTable,file_out_table, "w");
if(!outTable)
{
fprintf(stderr,
"Can't open output file '%s': %s\n",
file_out_table, strerror(errno));
return 1;
}
}
//end by yzhang
if(memory)//对内存数据进行编码或解码操作
{
return compress ?
memory_encode_file(in, out) : memory_decode_file(in, out);
}
if(compress) //编码操作change by yzhang
huffman_encode_file(in, out,outTable);
//step1:changed by yzhang from huffman_encode_file(in, out) to huffman_encode_file(in, out,outTable)
else
huffman_decode_file(in, out);
if(in)
fclose(in);
if(out)
fclose(out);
if(outTable)
fclose(outTable);
return 0;
}
Huffman编码主体程序:int huffman_encode_file(…)
int huffman_encode_file(FILE *in, FILE *out, FILE *out_Table) //Huffman编码
//step1:changed by yzhang for huffman statistics from (FILE *in, FILE *out) to (FILE *in, FILE *out, FILE *out_Table)
{
SymbolFrequencies sf;
SymbolEncoder *se;
huffman_node *root = NULL;
int rc;
unsigned int symbol_count;
//step2:add by yzhang for huffman statistics
huffman_stat hs;
//end by yzhang
/* Get the frequency of each symbol in the input file. *///第一遍扫描,得到文件各符号的出现频率
symbol_count = get_symbol_frequencies(&sf, in); //演示扫描完一遍文件后,统计字节出现的频率->SF指针数组的每个元素的构成
//step3:add by yzhang for huffman statistics,... get the frequency of each symbol
huffST_getSymFrequencies(&sf, &hs, symbol_count);
//end by yzhang
/* Build an optimal优化的 table from the symbolCount. */
se = calculate_huffman_codes(&sf);//根据得到的符号频率建立一棵Huffman树,还有Huffman码表
root = sf[0];//编完码表后Huffman树的根节点为sf[0],具体原因在后面的分析
//step3:add by yzhang for huffman statistics... output the statistics to file
huffST_getcodeword(se, &hs);
output_huffman_statistics(&hs, out_Table);
//end by yzhang
/* Scan the file again and, using the table
previously built, encode it into the output file. */
rewind(in);//回到文件头,准备进行第二遍扫描
rc = write_code_table(out, se, symbol_count);//先在输出文件中写入码表
if (rc == 0)
rc = do_file_encode(in, out, se);//写完码表后对文件字节按照码表进行编码
/* Free the Huffman tree. */
free_huffman_tree(root);
free_encoder(se);
return rc;
}
统计各字节符号出现频率函数 get_symbol_frequencies(…)
static unsigned int//统计各字节出现频率
get_symbol_frequencies(SymbolFrequencies *pSF, FILE *in)//psF 数组数据类型为树节点类型,存储空间为256个信源符号
{
int c;
unsigned int total_count = 0;//统计总样点数
/* 首先将所有符号出现的初始频率设为0 Set all frequencies to 0. */
init_frequencies(pSF);
/* Count the frequency of each symbol in the input file. */
while ((c = fgetc(in)) != EOF)//逐个读取字符,每次读取一个字节
//把一个字节看成一个信源符号,直到文件结束
{
unsigned char uc = c;//将读取的字符赋值给uc
if (!(*pSF)[uc])//如果还没有在数组里建立当前符号的信息,则说明这是第一次遇到的字符
(*pSF)[uc] = new_leaf_node(uc);//那么把这个符号设为一个叶节点,为其开辟内存空间
++(*pSF)[uc]->count;//不论该字符是不是第一次出现,对应符号数目即频数都要 +1
++total_count;//总计数值+1
}
return total_count;//返回统计的符号总数
}
建立Huffman树程序:calculate_huffman_codes(…)
//数组中存储的是指向结构体的指针
#define MAX_SYMBOLS 256 //node节点 code码字
typedef huffman_node* SymbolFrequencies[MAX_SYMBOLS];//信源符号数组,数据类型为之前定义过的树节点类型
typedef huffman_code* SymbolEncoder[MAX_SYMBOLS]; //编码后的码字数组,数据类型为之前定义过的码字类型
static SymbolEncoder*//建立Huffman树
calculate_huffman_codes(SymbolFrequencies * pSF)//创建一棵Huffman树的函数
{
unsigned int i = 0;
unsigned int n = 0;
huffman_node *m1 = NULL, *m2 = NULL;//定义两个临时Huffman_code指针变量
SymbolEncoder *pSE = NULL;
#if 1
printf("BEFORE SORT\n");//打印排序之前的符号信息
print_freqs(pSF); //【符号,频数】格式打印显示
#endif
/* Sort the symbol frequency array by ascending frequency. */
//将信源符号出现概率大小排序,小概率符号在前
qsort((*pSF), MAX_SYMBOLS, sizeof((*pSF)[0]), SFComp);
//先使用自定义的顺序对出现次数进行排序,使得下标为0的元素的count最小
#if 1
printf("AFTER SORT\n"); //打印排序之后的符号信息
print_freqs(pSF); //【符号,频数】格式打印显示
#endif
//获得文件中出现的信源符号总数
/* Get the number of symbols. */
for (n = 0; n < MAX_SYMBOLS && (*pSF)[n]; ++n)//统计下信源符号的真实种类数,因为一个文件中不一定256种字节都会出现
;
/*
* Construct a Huffman tree. This code is based
* on the algorithm given in Managing Gigabytes
* by Ian Witten et al, 2nd edition, page 34.
* Note that this implementation uses a simple
* count instead of probability.
*/
//每次合并树,是将2个子树进行一次合并。共有n个子树,最后合并结果是合并为概率为1的“大树”,故合并次数为n - 1
for (i = 0; i < n - 1; ++i)
{
//把出现次数最少的两个信源符号节点设为 m1,m2
/* Set m1 and m2 to the two subsets of least probability. */
m1 = (*pSF)[0];
m2 = (*pSF)[1];
//将两个小树合并成大树,需要将子树父指针指向新建的一个非叶指针节点,该节点的count值为两个子树的count相加
/* Replace m1 and m2 with a set {m1, m2} whose probability
* is the sum of that of m1 and m2. */
//然后合并这两个符号,把合并后的新节点设为这两个节点的父节点
(*pSF)[0] = m1->parent = m2->parent =new_nonleaf_node(m1->count + m2->count, m1, m2);
(*pSF)[1] = NULL;
//合并之后,原有的两个子节点需要删除,(*pSF)[0]存储新生成的码字,(*pSF)[1]置为空
//由于最小的两个频率数,进行了合并,所以整体顺序必须进行改变,故需要重新调用qsort()排序
/* Put newSet into the correct count position in pSF. */
qsort((*pSF), n, sizeof((*pSF)[0]), SFComp);
}
//树构造完成后,为码字数组分配内存空间并初始化
//pSE为指向指针数组的指针,为其开辟内存空间,并置零
/* Build the SymbolEncoder array from the tree. */
pSE = (SymbolEncoder*)malloc(sizeof(SymbolEncoder));
memset(pSE, 0, sizeof(SymbolEncoder));
build_symbol_encoder((*pSF)[0], pSE);
//从树根开始,为每个符号构建码字,从叶节点开始进行码字写入,实际应从根节点开始顺序为码字,所以要考虑倒序码字
return pSE;
}
static void//从根节点开始搜索找到树叶节点,然后逐层向上回到根节点,深度优先的递归搜索,遍历码树
build_symbol_encoder(huffman_node *subtree, SymbolEncoder *pSF)
{
if (subtree == NULL)//空树则返回
return;
//判断当前节点是否为根节点,遍历到编码结束
if (subtree->isLeaf)//如果是叶节点则生成码字
(*pSF)[subtree->symbol] = new_code(subtree);
else
{
//如果不是叶节点,继续遍历,采用中序遍历
build_symbol_encoder(subtree->zero, pSF);//先遍历左子树
build_symbol_encoder(subtree->one, pSF);//再遍历右子树
}
}
对码符号概率进行排序时调用快排函数qsort参数中自定义的排序规则函数SFComp()用以说明当概率为NULL即对应码符号没有出现过按照最小值来进行比较。
//实验中传参的SFComp为指向函数的指针
//SFcomp为指向函数的指针,
//SFcmop的两个形参类型为空类型指针
//调用时的pSF为 指向 指针数组的 指针!
//自定义的排序顺序函数,把字节数由小到大排序
static int SFComp(const void *p1, const void *p2){
//把两个排序元素设为自定义的树节点类型
const huffman_node *hn1 = *(const huffman_node**)p1;
const huffman_node *hn2 = *(const huffman_node**)p2;
//因为pSF是指针数组,所以这里传入的参数为指向指针的指针。
/* Sort all NULLs to the end. */
if (hn1 == NULL && hn2 == NULL)//如果两个节点都空,则返回相等。如果两个pSF类型都为空,返回0。
return 0;
if (hn1 == NULL) //如果第一个节点为空,则判断第二个节点大,返回正数。空节点视为极小数
return 1;
if (hn2 == NULL) //如果第二个节点为空,返回负数,判断第一个节点大。
return -1;
//如果都不空,则比较两个节点中的计数属性值,然后同上返回比较结果
if (hn1->count > hn2->count)//如果h1—count>h2-count,返回正数。我们要实现的是从小到大排序
return 1;
else if (hn1->count < hn2->count)//如果h1—countcount】 =【 hn2->counthn1】 返回0,保持原样,不进行位置调整
}
压缩文件头部首先写入Huffman码表:write_code_table(…)
static int//写码表
write_code_table(FILE* out, SymbolEncoder *se, unsigned int symbol_count)
{
unsigned long i, count = 0;
//还是要先统计下真实的码字种类,不一定256种都有
/* Determine the number of entries in se. */
//通过码表类型计算出现了多少码符号count
for (i = 0; i < MAX_SYMBOLS; ++i)
{
if ((*se)[i])
++count;
}
//把字节种类数和字节总数变成大端保存的形式,写入文件中
/* Write the number of entries in network byte order. */
i = htonl(count); //在网络传输中,采用big-endian序,对于0x0A0B0C0D ,传输顺序就是0A 0B 0C 0D ,
//因此big-endian作为network byte order,little-endian作为host byte order。
//little-endian的优势在于unsigned char/short/int/long类型转换时,存储位置无需改变
if (fwrite(&i, sizeof(i), 1, out) != 1)
return 1;
//改变字节序写入码元数,即上文提到的‘样本数’,挨着写入文件头
/* Write the number of bytes that will be encoded. */
symbol_count = htonl(symbol_count);
if (fwrite(&symbol_count, sizeof(symbol_count), 1, out) != 1)
return 1;
//然后开始写入码表
/* Write the entries. */
for (i = 0; i < MAX_SYMBOLS; ++i)
{
huffman_code *p = (*se)[i];
if (p)
{
unsigned int numbytes;
/* Write the 1 byte symbol. 写入 1byte 的符号*/
fputc((unsigned char)i, out);//码表中有三种数据,先写入字节符号
/* Write the 1 byte code bit length. 写入 1byte 大小的码长数*/
fputc(p->numbits, out);//再写入码长
//最后得到字节数,写入码字
/* Write the code bytes.*/
numbytes = numbytes_from_numbits(p->numbits);
if (fwrite(p->bits, 1, numbytes, out) != numbytes)//写入符号对应的码字
return 1;
}
}
return 0;
}
//由比特位长度得到字节数,除以8取整,如果还有余数说明还要再加一个字节
//加入码长有25个bit,也需要4个Byte来传送(8*3+1)
static unsigned long
numbytes_from_numbits(unsigned long numbits)
{
return numbits / 8 + (numbits % 8 ? 1 : 0);
}
第二次扫描,对文件进行编码:do_file_encode(…)
static int//第二次扫描,对源文件进行编码并输出
do_file_encode(FILE* in, FILE* out, SymbolEncoder *se)
{
unsigned char curbyte = 0;
unsigned char curbit = 0;
int c;
//逐字节读取待编码的文件,要找到当前符号(字节)uc对应的码字code,只需要把uc作为码字数组se的下标即可
while ((c = fgetc(in)) != EOF)//挨个字符读入
{
unsigned char uc = (unsigned char)c;//对读入的字符进行查表
huffman_code *code = (*se)[uc];//进行查表操作
unsigned long i;
for (i = 0; i < code->numbits; ++i)
{
//把码字中的一个比特位放到编码字节的相应位置
//操作与上文构建码表操作类似,所读出的比特右移curbit位后,与先前的操作相与
/* Add the current bit to curbyte. */
curbyte |= get_bit(code->bits, i) << curbit;
/* If this byte is filled up then write it
* out and reset the curbit and curbyte. */
//如果curbit已经凑够一个字节则进行写入文件操作,且curbit与curbit置0
if (++curbit == 8)
{
fputc(curbyte, out);
curbyte = 0;
curbit = 0;
}
}
}
/*
* If there is data in curbyte that has not been
* output yet, which means that the last encoded
* character did not fall on a byte boundary,
* then output it.
*/
//处理一下最后一个字节的编码不足一字节的情况
//假如最后一个符号的编码不足以凑够8个字节也需要强行写入(否则就要被丢弃了)
if (curbit > 0)
fputc(curbyte, out);
return 0;
}
/*
* get_bit returns the ith bit in the bits array
* in the 0th position of the return value.
*/
//取出码字的第i位,第 i 位在第 i/8 字节的第 i%8 位,把这一位移到字节最低位处,和 0000 0001 做与操作,从而只留下这一位,返回*
//bit[i/8]中的i/8用于确定索取的位数在第几个字节中,譬如i = 10,则处在bit[1]中。
//取出来的字节,需要右移。右移位数:i%8
//譬如i = 10,则右移两位。
//右移后结果与000000001相与,得到返回的bit位
static unsigned char
get_bit(unsigned char* bits, unsigned long i)
{//从bit[]中获取一位数据
return (bits[i / 8] >> i % 8) & 1;
}
生成码字:new_code(…)
生成叶节点:new_leaf_node(…)
生成非叶节点:new_nonleaf_node(…)
/*
* new_code builds a huffman_code from a leaf in
* a Huffman tree.
*/
static huffman_code*
new_code(const huffman_node* leaf)//生成码字
{
/* Build the huffman code by walking up to
* the root node and then reversing the bits,
* since the Huffman code is calculated by
* walking down the tree. */
//码字的位数numbits也就是数从下到上的第几层,还有保存码字的数组bits
unsigned long numbits = 0;//定义码长,定义码字位数numbits,同时它也表示树从上到下的第几层
unsigned char* bits = NULL;//码字首地址,bits表示存码字的数组
huffman_code *p;
while (leaf && leaf->parent)//自下而上,直至找到到根节点
{
//那么得到当前节点的父节点,由码字位数得到码字在字节中的位置和码字的字节数
huffman_node *parent = leaf->parent;//得到该节点父节点,由码字位数可以得到码字的位置和码字的字节
unsigned char cur_bit = (unsigned char)(numbits % 8);
//当前所编码bit在字节中的位置
unsigned long cur_byte = numbits / 8;
//当前是第几个字节Byte
/* If we need another byte to hold the code,
then allocate it. */
if (cur_bit == 0)//意味着开始新Byte的编码
///如果比特位数为0,说明到了下一个字节,新建一个字节保存后面的码字
{
size_t newSize = cur_byte + 1;//新的字节数为当前字节数+1,size_t 即为 unsigned int 类型
bits = (char*)realloc(bits, newSize);//数组按照新的字节数重新分配空间
bits[newSize - 1] = 0; //并把新增加的字节设为0/* Initialize the new byte. */
}
/* If a one must be added then or it in. If a zero
* must be added then do nothing, since the byte
* was initialized to zero. */
if (leaf == parent->one)//如果是右子节点,按照Huffman树左0右1的原则,应当把当前字节中当前位置1
//先把1右移到当前位(cur_bit)位置,再把当前字节(bits[cur_byte])与移位后的1做或操作
bits[cur_byte] |= 1 << cur_bit;
/*如果当前节点为父节点的右子树,则需要将码字对应位置置1。
* 将1左移cur_bit位,cur_bit位当前的编的位置
* 如果当前节点为父节点的左子树,不需要操作,因为初始化时的8bit已经为0*/
++numbits;//码长+1 //然后码字的位数加1
leaf = parent;//节点顺序往上 ////下一位码字在父节点所在的那一层
}
//回到根之后编码完毕,对码字进行倒序
if (bits)
reverse_bits(bits, numbits);
//使用的Huffman是自顶向下,而以上方法是从叶节点向上的方向遍历编码,所以需要整个码字逆序
//倒序后,输出码字数组
p = (huffman_code*)malloc(sizeof(huffman_code));
p->numbits = numbits;
p->bits = bits;
return p;
//返回生成的码字节点
//构建一个Huffman_code 结构,返回给上层函数
}
static huffman_node*
new_leaf_node(unsigned char symbol)//建立叶节点
{
huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node));//开辟空间
p->isLeaf = 1;//叶节点,标识符置1
p->symbol = symbol;//将第一次遇到的字符存入该节点的symbol值中
p->count = 0;//初始化字符出现频数值为0
p->parent = 0;//初始化父亲节点为0
return p;//返回创建的Huffman节点
}
static huffman_node*//建立一个非叶节点的数据类型
new_nonleaf_node(unsigned long count, huffman_node *zero, huffman_node *one)
{
huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node));//分配一个节点的存储空间
p->isLeaf = 0;//非叶节点,标识符置0
p->count = count;//非叶节点出现的频数值为两个子树传递上来的count总和
p->zero = zero;//左子树叶节点
p->one = one;//右子树叶节点
p->parent = 0;//父亲节点尚且为空
return p;
}
##Huffman解码流程
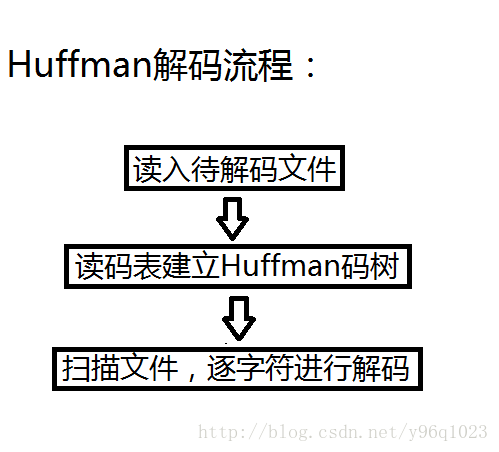
###对解码程序代码进行注释分析如下:
读取压缩后文件首部Huffman码表成粗:read_code_table(…)
/*
* read_code_table builds a Huffman tree from the code
* in the in file. This function returns NULL on error.
* The returned value should be freed with free_huffman_tree.
*/
static huffman_node*//读码表
read_code_table(FILE* in, unsigned int *pDataBytes)
{
huffman_node *root = new_nonleaf_node(0, NULL, NULL);
unsigned int count;
/* Read the number of entries.
(it is stored in network byte order). */
//读文件和写文件一样,按照小端方式读
if (fread(&count, sizeof(count), 1, in) != 1)
{
free_huffman_tree(root);
return NULL;
}
//所以按照大端方式存放的数据count,再转换一次就得到了正确结果
count = ntohl(count);
//ntohl()是将一个无符号长整形数从网络字节顺序转换为主机字节顺序
//从big-endian转化为little-endian
/* Read the number of data bytes this encoding represents. */
if (fread(pDataBytes, sizeof(*pDataBytes), 1, in) != 1)
{
free_huffman_tree(root);
return NULL;
}
*pDataBytes = ntohl(*pDataBytes);
// 原文件的总字节数pDataBytes也由littleendian转化为bigendian
/* Read the entries. */
//读完这些后,文件指针指向了码表开头,依次读取码表中的每一项,每一项由符号,码长,码字三种数据组成
while (count-- > 0)
{
int c;
unsigned int curbit;
unsigned char symbol;
unsigned char numbits;
unsigned char numbytes;
unsigned char *bytes;
huffman_node *p = root;
if ((c = fgetc(in)) == EOF)//一次读一个字节,第一个字节是信源符号symbol
{
free_huffman_tree(root);
return NULL;
}
symbol = (unsigned char)c;
if ((c = fgetc(in)) == EOF)//第二个字节是码长数据numbits
{
free_huffman_tree(root);
return NULL;
}
numbits = (unsigned char)c;
//计算出这样一个码长需要多少个字节(numbytes个)保存,开辟与字节数对应的空间
numbytes = (unsigned char)numbytes_from_numbits(numbits);
bytes = (unsigned char*)malloc(numbytes);
if (fread(bytes, 1, numbytes, in) != numbytes)//然后读取numbytes个字节得到码字bytes
{
free(bytes);
free_huffman_tree(root);
return NULL;
}
/*
* Add the entry to the Huffman tree. The value
* of the current bit is used switch between
* zero and one child nodes in the tree. New nodes
* are added as needed in the tree.
*/
for (curbit = 0; curbit < numbits; ++curbit)//读完码表码符号三种数据后,开始由码字建立Huffman树
{
if (get_bit(bytes, curbit))//如果码字中的当前位为1
{
if (p->one == NULL)//那么没有右子节点则新建一个右子节点
{//如果是最后一位,就建立树叶节点,否则就当做一个父节点,后续建立他的子节点
p->one = curbit == (unsigned char)(numbits - 1)
? new_leaf_node (symbol)
: new_nonleaf_node (0, NULL, NULL);
p->one->parent = p;//设置好新建节点的父节点
}
p = p->one;//不管右子节点是不是新建的,都要把这个节点当成父节点,以便建立它后续的子节点
}
else//如果码字中的当前位为0
{
if (p->zero == NULL)//那么应该建立一个左子节点(如果没有的话)
{
p->zero = curbit == (unsigned char)(numbits - 1)
//同理,选择节点类型并确定节点之间的关系
? new_leaf_node(symbol)
: new_nonleaf_node(0, NULL, NULL);
p->zero->parent = p;
}
p = p->zero;
}
}
free(bytes);//和编码一样,只要有最上面的根节点就能遍历整棵树
}
return root;
}
对文件逐字符进行Huffman解码程序:huffman_decode_file(…)
int huffman_decode_file(FILE *in, FILE *out)//Huffman解码
{
huffman_node *root, *p;
int c;
unsigned int data_count;
/* Read the Huffman code table. */
root = read_code_table(in, &data_count);//打开文件后首先读入码表,建立Huffman树,并且获取原文件的字节数
if (!root)
return 1;
/* Decode the file. */
p = root;
while (data_count > 0 && (c = fgetc(in)) != EOF)//准备好码树之后,一次读一个字节进行解码
{
unsigned char byte = (unsigned char)c;
unsigned char mask = 1;
//mask负责提取字节中的每一位,提取完之后向左移动一位来提取下一位。因此移动8位之后变成0,循环退出,读下一个字节
while (data_count > 0 && mask)
{
//如果当前字节为0,就转到左子树,否则转到右子树
p = byte & mask ? p->one : p->zero;
mask <<= 1;//准备读下一个字节
if (p->isLeaf)//如果走到了叶节点
{
fputc(p->symbol, out);//就输出叶节点中存储的符号
p = root;//然后转到根节点,再从头读下一个码字
--data_count;//而且剩下没解码的符号数-1
}
}
}
free_huffman_tree(root);
return 0;
}
##测试统计
选择了十种不同格式类型的文件,使用Huffman编码器进行压缩得到输出的压缩比特流文件,添加代码进行结果统计,对各种不同格式的文件进行压缩效率的分析。结果分析包含下述三项:
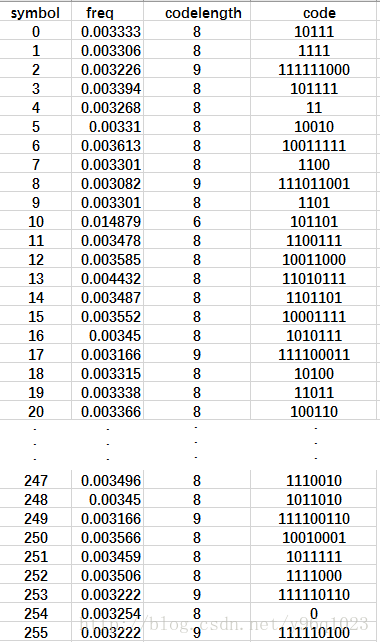
1. 程序结果运行输出,包括码符号、文件中出现概率、码长、编码结果这几项,以测试文件test1.mp3的编码结果为展示如下:
测试文件类型以及生成的Huf文件、统计数据文件如图:
2. 将十个样本文件的符号分布概率绘制成二维柱状统计图,将测试文件的运行结果导入Excel中计算平均码长、信源熵以及经过Huffman编码后的文件压缩比,结果如下所示:
{压缩比=输入流码率/输出流码率}
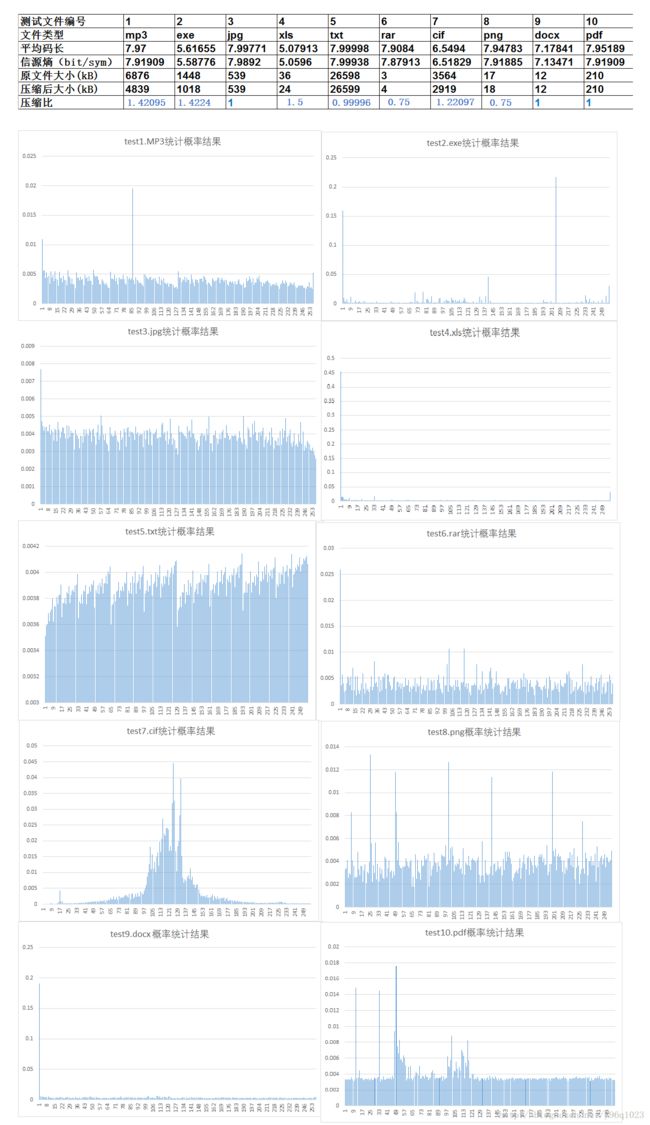
#实验结果分析
- 原始文件的概率分布越不均匀,通过Huffman编码后得到文件的压缩比越高,反之若原始概率分布趋近于均匀等概则压缩效果就不会很好,甚至会因为码表太大导致压缩后的文件更小即压缩比小于1的情况。原因是因为根据香农第一定理即无失真信源编码定理,二进制码信源符号,平均码长的下界为信源熵。当信源符号接近等概分布时,信源熵最大,此时的平均码长已接近下限,文件再没有压缩的余地了。
- 解码器:遍历码表->生成Huffman树,有明显的缺点:码表大,解码效率不均,解码速度慢。 提高效率往往会以牺牲存储为代价,于是为了解决这个矛盾就衍生出新的数据结构。