机器学习笔记025 | 算法诊断的代码实现

我们有一些大坝水位和水量溢出的历史数据，想要对未来进行一些预测。

数据分为三个集合，分别是：

训练集：( X, y )
验证集：( X_val, y_val )
测试集：( X_test, y_test )

训练集的数据打印出来是这样的：

我们使用线性回归的方式进行预测，得到的预测曲线是这样的：

显然，这样的曲线存在较大的偏差，不能很好的拟合数据。

对其学习曲线的打印结果，也正如我们的预料：

随着训练样本数量的增加，训练集的误差增加，而验证集的误差减少，两者的差距在缩小。

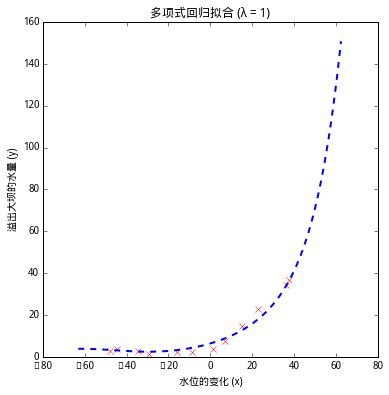
而如果使用多项式回归进行预测，得到的预测曲线是这样的：

正则化参数为0：

预测曲线

学习曲线

正则化参数为1：

预测曲线

学习曲线

正则化参数为100：

预测曲线

学习曲线

我们有 {0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10}这样的一些正则化参数列表，想要找到验证集最小的正则化参数，绘画出来的学习曲线如下：

通过对比我们可以知道，当 λ 在3左右的时候，验证集的误差是最小的。

主要部分代码如下，更多代码请点击阅读原文查看：

线性回归的代价函数：

# 代价函数
def costFunction(theta, X, y,mylambda):
    # 样本数量
    m = y.size 
    # 参数的拷贝
    tmp_theta = theta.reshape(X.shape[1],1).copy() 
    # 预测函数
    h = dot(X,tmp_theta)
    # 代价函数
    J = 1.0/2/m*sum((h-y)**2)+1.0*mylambda/2/m*sum(tmp_theta[1:]**2)
    
    if np.isnan(J):
        return np.inf
    return J

梯度：

# 梯度
def gradient(theta, X, y,mylambda):
    # 样本数量
    m = X.shape[0]
    # 参数的拷贝
    tmp_theta = theta.reshape(X.shape[1],1).copy()  
    # 预测函数
    h = dot(X,tmp_theta)
    # 梯度计算
    tmp_theta[0]=0
    grad = 1.0/m*X.T.dot(h-y)+1.0*mylambda/m*tmp_theta
    grad = grad.flatten()
    return grad

训练数据：

# 训练数据获得最优拟合参数
def trainLinearReg(X, y, mylambda):
    initial_theta = np.zeros(X.shape[1])
    opts = {'maxiter': 50}
    result = optimize.minimize(costFunction, initial_theta, args=(X, y, mylambda), method='CG', jac=gradient, tol=None, callback=None, options=opts)
    theta = result.x
    
    return theta

循环计算不同正则化参数下的训练集和验证集误差：

# 返回正则化参数与训练集和验证集的误差
def validationCurve(X, y, Xval, yval):
    lambda_vec = [0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10]
    #lambda_vec = [0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24]

    error_train = np.zeros(len(lambda_vec))
    error_val   = np.zeros(len(lambda_vec))
    
    for i in range(len(lambda_vec)):
        mylambda = lambda_vec[i]
        theta = trainLinearReg(X, y, mylambda)
        error_train[i] = costFunction(theta, X, y, 0)
        error_val[i] = costFunction(theta, Xval, yval, 0)
        
    return lambda_vec,error_train,error_val

文章转载自公众号：止一之路