强化学习——简介

前言

我最先了解到强化学习还是看见论文中有使用强化学习算法去玩游戏，并且玩得比人类还好，之后AlphaGo系列的围棋机器人战胜世界高手也让我更进一步知道了强化学习的威力。本系列强化学习笔记将以DeepMind AlphaGo的主要研究人员David Silver《深度强化学习》视频公开课以及强化学习圣经——《Reinforcement Learning：An Introduction》(Second edition)的内容为主，并穿插介绍一些我学习过程中的实践案例。

强化学习的范畴

机器学习，深度学习大家都很熟悉，实际上强化学习也属于机器学习的一种，其关系如下图所示

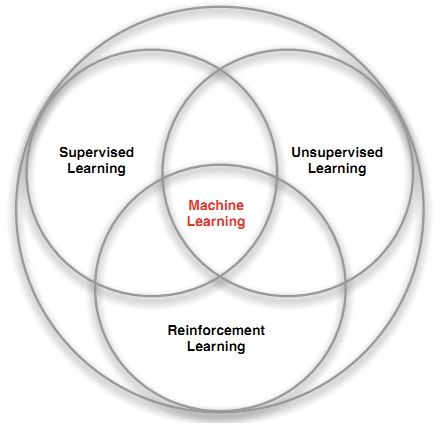
之所以强化学习有别于其他机器学习方法，主要体现在以下四点：

• 没有监督数据，只有奖励信号；
• 反馈的信号具有滞后性，不及时；
• 时间（序列）是一个重要因素；
• 当前的动作影响后续接收的数据。

强化学习也是一种多学科交叉的产物，它本身是一种决策科学，所以在许多学科分支中都可以找到它的身影。

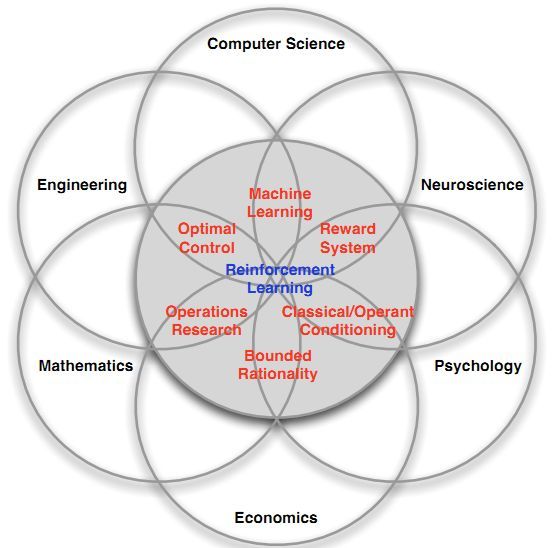
所以强化学习应用广泛，比如：直升机特技飞行、游戏AI、投资管理、发电站控制、让机器人模仿人类行走等。

强化学习的提出

强化学习就是学习如何根据一个环境状态去决定如何行动，使得最后的奖励最大。强化学习中两个最重要的特征就是试错（trial-and-error）和滞后奖励（delayed reward）。比如在训练走迷宫的AI时，我们的学习者（Agent）不会被告知下一步该如何走，而是通过尝试不同的走法，得到不同的奖励。但是，这个奖励可能不会立即得到，比如得走出迷宫以后才能得到奖励。

奖励（Rewards）

• 奖励是一个标量反馈信号；
• 表明agent在时刻的表现如何；
• agent的任务就是最大化积累的奖励。

序列决策(Sequential Decision Making)

• 目标：选择一个可以使未来奖励最大的动作(actions)；
• 这个动作可能产生一个长远的结果；
• 奖励可能有滞后性；
• 可能牺牲眼前的奖励而获得长远的奖励更有用（比如投资理财）。

学习者和环境(Agent &Environment)

如下图所示，图中的人脑可以看做Agent，地球可以看做Environment。每个时刻$t$ ,Agent得到对环境的观测$O_t$，并执行动作 $A_t$ ，接着环境因为Agent的动作产生新的观测 $O_{t+1}$ ，同时反馈给Agent一个标量值的奖励 $R_t$ 。

历史和状态(history&state)

在Agent和环境进行交互的时候，会产生一连串的观测，动作和奖励，即历史(history)
$$H_t=O_1,R_1,A_1,\dots ,A_{t-1},O_t,R_t$$
将要发生的事情（Agent要做什么动作、环境将产生什么观测和奖励），完全取决于历史。而状态(state)就是决定将要发生事情的信息。通常状态是历史的函数：
$$S_t=f\left(H_t\right)$$

环境状态

环境状态 $S_t^e$ 是环境的一种私有呈现，它包含了用于下一步产生观测和奖励的全部信息，而这些信息对Agent来说通常是不可见的，即使可见也通常含有很多无关的信息。

Agent状态

Agent状态 $S_t^a$ 是Agent内部的一种呈现。包含了用于产生下一步动作的全部信息，这些信息就是强化学习算法需要的信息，它可以由历史的某种函数所表示：
$$S_t^a=f\left(H_t\right)$$

信息状态

信息状态又称为马尔科夫状态(Markov state)，它包含了来自历史所有有用的信息。一个状态具有马尔科夫性质，当且仅当
$$\mathbb{P}\left[S_{t+1}|S_t\right]=\mathbb{P}\left[S_{t+1}|S_1,\dots ,S_t\right]$$
也就是说，如果信息状态是可知的，那么所有历史信息都可以丢掉，仅需要前一个状态的信息。比如环境状态和历史状态就具有马尔科夫性质。

完全观测环境

完全观测（Full observability）环境即Agent可以直接观测环境状态：
$$O_t=S_t^a=S_t^e$$
这也是我所说的强化学习形式——马尔科夫决策过程（Markov decision process, MDP）

部分观测环境

部分观测（Partial observability）环境即Agent不能直接观测环境状态，此时
$$S_t^a\ne S_t^e$$
比如下面几个例子：

• 一个可拍照的机器人个体对于其周围环境的观测并不能说明其绝对位置，它必须自己去估计自己的绝对位置，而绝对位置则是非常重要的环境状态特征之一；
• 一个交易员只能看到当前的交易价格，但他不知道价格趋势，什么推动了价格的变化等；
• 一个扑克牌玩家只能看到自己的牌和其他已经出过的牌，而不知道整个环境（包括对手的牌）状态。

这就是部分观测马尔科夫决策过程（Partial observable Markov decision process, POMDP）。Agent必须自己去构建 $S_t^a$ ，比如

• 记住全部历史： $S_t^a=H_t$
• 创建环境状态的概率分布： $S_t^a=\left(\mathbb{P}\left[S_t^e=s^1\right],\dots ,\mathbb{P}\left[S_t^e=s^n\right]\right)$ ，这个概率向量决定了状态。
• 循环神经网络（RNN）： $S_t^a=\sigma \left(S_{t-1}^a{W}_s+O_t{W}_0\right)$ ，即使用线性组合的方式把最近的agent状态与最近的观测结合起来，就可以得到最新的状态。

Agent的组成元素

策略（Policy）

策略定义了agent的行为方式，是从状态到行为的一个映射，策略可以是一个简单的函数 $a=\pi (s)$，也可以是一个查询表或者就是随机的$\pi (a|s)=\mathbb{P}\left(A_t=a|S_t=s\right)$ 。

值函数（Value Function）

值函数是一个对未来奖励的预测，用来评价当前状态的好坏程度。比如，当Agent面临状态1和状态2（对应动作1和动作2）时，该如何选择？当然是选择奖励最大的，而值函数就是用来预测这个奖励的。数学形式如下
$$v_{\pi }(s)=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots |S_t=s\right]$$
可见，值函数是基于策略的。

模型（Model）

模型并不是环境本身，但是对于预测环境变化很有用处，这有利于Agent决定下一步的行动。模型至少要解决两个问题：一是状态转化概率，即预测下一个可能状态发生的概率：
$$P_{s{s}^{\prime }}^a=\mathbb{P}\left[S_{t+1}=s^{\prime }|S_t=s,A_t=a\right]$$
另一个是预测可能获得的即时奖励：
$$R_{s{s}^{\prime }}^a=\mathbb{E}\left[R_{t+1}|S_t=s,A_t=a\right]$$
但是，模型并不是构建一个个体所必需的。

Agent分类

下面这张图，大概就把分类说清楚了。即在有无环境模型的分类下分为基于策略的或者基于值函数的或者基于两者一起的。

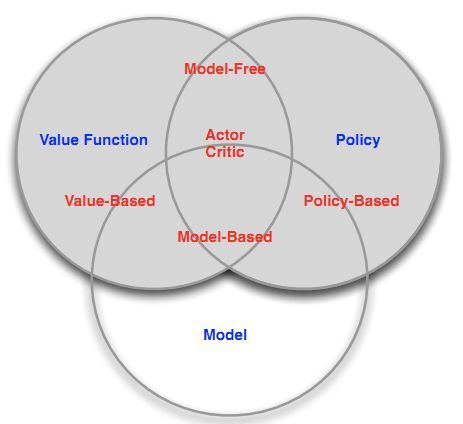
学习和规划(Learning & Planning)

根据初始环境模型是否已知决定了强化学习的两种方式：学习和规划。当初始环境未知时，agent需要与环境不断交互，从而提升策略。而环境模型已知时，agent就不需要与环境进行交互，只需根据模型进行计算即可，从未提升策略。

探索和利用(Exploration & Exploitation)

强化学习类似于一个试错的学习，个体需要从其与环境的交互中发现一个好的策略，同时又不至于在试错的过程中丢失太多的奖励。探索和利用是个体进行决策时需要平衡的两个方面。

一个形象的比方是，当你去一个餐馆吃饭，“探索”意味着你对尝试新餐厅感兴趣，很可能会去一家以前没有去过的新餐厅体验，“利用”则意味着你就在以往吃过的餐厅中挑一家比较喜欢的，而不去尝试以前没去过的餐厅。这两种做法通常是一对矛盾，但对解决强化学习问题又都非常重要。

预测和控制(Prediction & Control)

在强化学习里，我们经常需要先解决关于预测（prediction）的问题，而后在此基础上解决关于控制（Control）的问题。预测：给定一个策略，评价未来。可以看成是求解在给定策略下的价值函数（value function）的过程。控制：找到一个好的策略来最大化未来的奖励。

---

欢迎关注我的公众号“野风同学”，一个程序员的自我成长之路，持续分享机器学习基础与应用、LeetCode面试算法和Python基础与应用等技术干货文章，同时也经常推荐高质量软件工具、网站和书籍。