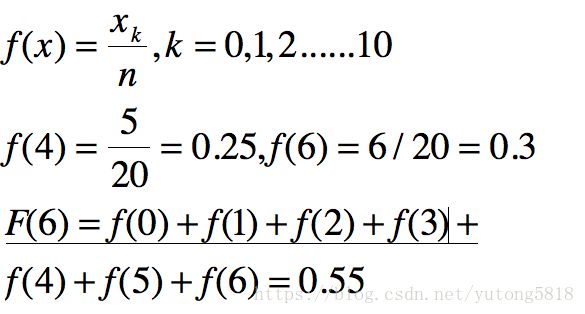MATLAB中histeq的原理以及自写的具体实现函数
1.什么是直方图?
直方图是数字图像处理中一个简单而重要的常用工具,它从总体上刻画了一幅图像的灰度内容。
具体来说,直方图描述的是图像中具有各灰度级的出现的概率(像素的个数),其横坐标为灰度级,纵坐标为图像中具有该灰度级的像素个数。由于灰度级的大小为0-255,故横坐标的数值范围为0-255.
其语法格式为:
J=histeq(I,hgram);
J=histeq(I,n);
[J,T]=histeq(I);
注:hgram为归一化(各元素均在[0,1]上)的灰度直方图。
[J,T]=histeq(I);返回图像J的同时也返回变换向量。
2.直方图的基本数学原理
直方图均衡化方法可以产生一幅灰度级分布概率均匀的图像。以概率论中的概率密度和分布函数为基础,在这里我们举例来理解直方图的概念。
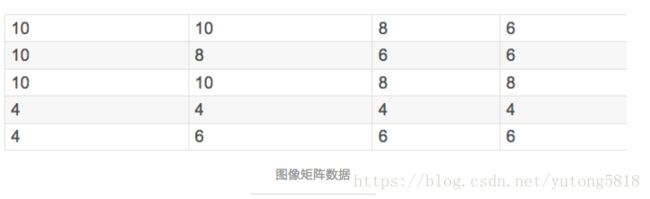
比如有如下图像矩阵数据
代表着数值为4的个数有5个,数值为6的个数有6个,数值为8的个数有4个,数值为10的个数有5个
则直方图为
真实的直方图是灰度级是从0-255的,上图应该讲灰度级为0的也标注出来才是正确的。
原图中,灰度级为6的大小为6,直方图均衡化之后,灰度级为6的大小为20*(0.25+0.55)=14.
通过上述原理,我们不难发现,概率密度表示对应的某一灰度级数在图片中出现的概率,某一灰度级数的分布函数值则表示小于等于该灰度级数的所有灰度值在图片中所占概率。(概率论课本上的)
正如前文所述,直方图均衡化作用在于将原始直方图变为更均匀分布的图片。因此,基于上述数学原理,我们便可在此基础上推出直方图均衡化的实现原理:
用分布函数代替概率密度函数,实现熵最大化。
自制函数为:
f=imread('tire.tif');[m,n]=size(f);
f1=im2uint8(ones(m,n));
h=imhist(f);
I=length(h);
%概率密度
fx=h/numel(f);
%分布函数
FX=cumsum(fx);
%获得均衡化之后的灰度直方图
j=FX.*256;
J=round(j);%由于灰度级为1-256之间的整数,
%故需对拓展之后的灰度灰度级数取整才有意义。
%将拓展后的的灰度级数对应映射到图片中。
%由于灰度级数为1-256之间的整数,故需对扩展之后的灰度级数取整才有意义,
%得到的J矩阵为1X256大小,表示扩展之前的灰度级数,其中每个级数对应 %元素的值为该灰度级数扩展后的灰度级数值。如J(2)=24,表示原始灰%%%%度 直方 图 为2灰度值
%的地方经灰度扩展后其灰度值为24
for i=1:I %I=256
old=find(J==i); %找出扩展后的级数对应的扩展前的级数
L=length(old);
for k=1:L %m每一个n*n的
oldlocation=find(f==(old(k)-1));%找到拓展前的灰度级数对应的像素点
f1(oldlocation)=i;
end
end
subplot(1,2,1),imhist(f1)
subplot(1,2,2),imshow(f1);
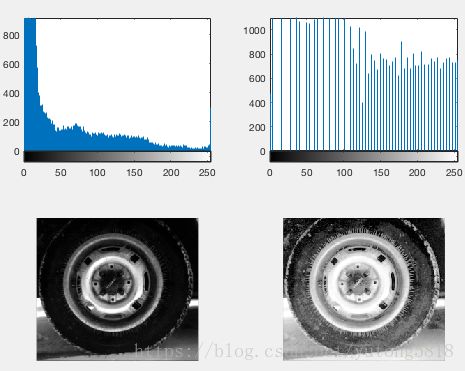
在这我们以tire.tif这张图片作为例子
如果用MATLAB自带的函数实现,如下:
x=imread('tire.tif');
y=histeq(x);
subplot(2,2,1),imhist(x);
subplot(2,2,2),imhist(y);
subplot(2,2,3),imshow(x);
subplot(2,2,4),imshow(y);
结果如图:
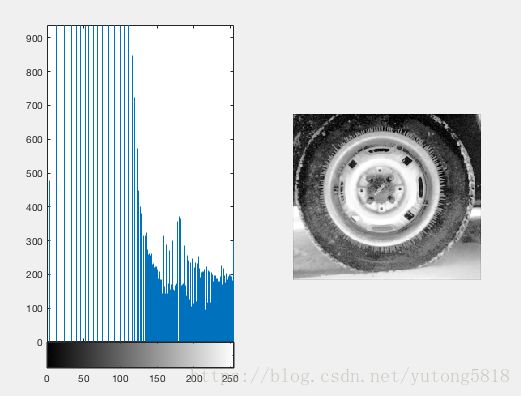
再用我以直方图均衡化为原理自制的函数运行,结果如下图
可以发现均衡化之后的图片与原图几乎一致,但是所呈现的直方图,在灰度级150之后均衡效果很差,需要改善。