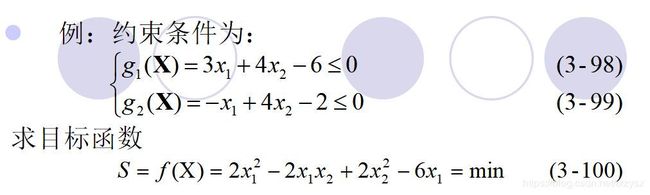线性规划单纯形法、大M法,非线性规划的拉格朗日乘子法的手推法,excel、python编程以及python包编程
线性规划单纯形法、大M法,非线性规划的拉格朗日乘子法的手推法,excel、python编程以及python包编程
目录
- (1) 线性规划
- 单纯形法概念
- 定义
- 标准形式
- 步骤
- 大M法概念
- 定义
- 步骤
- EXCEL求解
- 单纯形法
- 大M法
- Python编程
- Python包编程
- (2)非线性规划
- 非线性规划的拉格朗日乘子法的Excel,python编码和python包编码
- 等式约束的拉格朗日乘子法
- 不等式约束的拉格朗日乘子法
- 无约束的拉格朗日乘子法(KKT条件下)
- 手推法
- python包编程
- 参考文献
(1) 线性规划
单纯形法概念
定义
一般线性规划问题中当线性方程组的变量数大于方程个数,这时会有不定数量的解,而单纯形法是求解线性规划问题的通用方法。
具体步骤是,从线性方程组找出一个个的单纯形,每一个单纯形可以求得一组解,然后再判断该解使目标函数值是增大还是变小了,决定下一步选择的单纯形。通过优化迭代,直到目标函数实现最大或最小值。
换而言之,单纯形法就是秉承“保证每一次迭代比前一次更优”的基本思想:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进后更优的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。如果问题无最优解,也可用此法判别。

标准形式
由于目标函数和约束条件内容和形式上的差别,线性规划问题可以有多种表达式。因此,为了便于讨论和制定统一的算法,在制定单纯形法时,规定使用单纯形法求解的线性规划问题需要有一个标准形式,它有下面三个特征:
(1) 标准形式目标函数统一为求极大值或极小值,但单纯形法主要用来求解极大值;
(2) 所有约束条件(除非负条件外)都是等式,约束条件右端常数项bi全为非负值;
(3) 所有变量的取值全为非负值。
下式为满足上述特征的线性规划问题的标准形式
 其中,目标函数中的变量xj(x1,x2,…xn)称为决策变量(控制变量),它的取值受m项资源的限制,它的系数称为价值系数cj。s.t.括号下的内容是约束条件,用bi(i=1,···,m)表示第i种资源的拥有量,用aij表示变量xj取值为1个单位时所消耗或含有的第i种资源的数量,通常称aij为技术系数或工艺系数。
其中,目标函数中的变量xj(x1,x2,…xn)称为决策变量(控制变量),它的取值受m项资源的限制,它的系数称为价值系数cj。s.t.括号下的内容是约束条件,用bi(i=1,···,m)表示第i种资源的拥有量,用aij表示变量xj取值为1个单位时所消耗或含有的第i种资源的数量,通常称aij为技术系数或工艺系数。
除非负条件外的n个约束条件所组成的n元方程组,若可解可求出n个变量xj的值。求出的n个变量所构成的列向量X=(x1,···xn)T,若能再满足非负条件(即决策变量满足所有约束条件),称为线性规则问题的可行解。使得目标函数值z达到max最大的可行解即为最优解,求解线性规划问题的目的就是要找出目标函数的最优解。
下图为上式标准形式的线性规划问题的展开型:

步骤
①把线性规划问题的约束方程组表达成典范型方程组,典范型方程组要实现变量转换(所有变量为非负)、目标转换(统一为求极大值,若求极小值可乘以(-1))、约束转换(由不等式转化为等式)。然后,找出基本可行解作为初始基可行解。列出初始单纯形表。
②若基本可行解不存在,即约束条件有矛盾,则问题无解。
③若基本可行解存在,从初始基可行解作为起点,根据最优性条件和可行性条件,引入非基变量取代某一基变量,找出目标函数值更优的另一基本可行解。
④按步骤3进行迭代,直到对应检验数满足最优性条件(这时目标函数值不能再改善),即得到问题的最优解。
⑤若迭代过程中发现问题的目标函数值无界,则终止迭代。
大M法概念
定义
大M法(big M method)是线性规划问题的约束条件(=)等式或(≥)大于型时,使用人工变量法后,寻找其初始基可行解的一种方法
在线性规划问题的约束条件中加人工变量后,要求在目标函数中相应地添加认为的M或一M为系数的项。在极大化问题中,对人工变量赋于一M作为其系数;在极小化问题中,对人工变量赋于一个M作为其系数,M为一任意大(而非无穷大)的正数。把M看作一个代数符号参与运算,用单纯形法求解,故称此方法为大M法
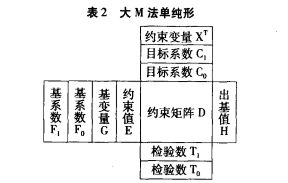
步骤
应用单纯形法在改进目标函数的过程中,如果原问题存在最优解,必然使人工变量逐步变为非基变量,或使其值为零。否则,目标函数值将不可能达到最小或最大。在迭代过程中,若全部人工变量变成非基变量,则可把人工变量所在的列从单纯形表中删去,此时便找到原问题的一个初始基可行解。若此基可行解不是原问题的最优解,则继续迭代,直至所有的检验数都小于等于0,求得最优解为止
EXCEL求解
单纯形法
步骤
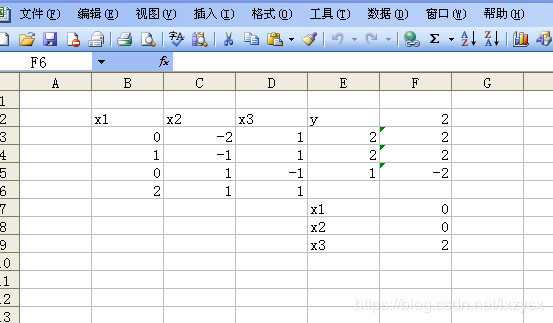
先输入B2到E9的内容
然后在F2:F5输入下面的算式
F2 =MMULT(B6:D6,F7:F9)
F3 =MMULT(B3:D3,F7:F9)
F4 =MMULT(B4:D4,F7:F9)
F5 =MMULT(B5:D5,F7:F9)
 选择工具—规划求解
选择工具—规划求解

设置下面的参数
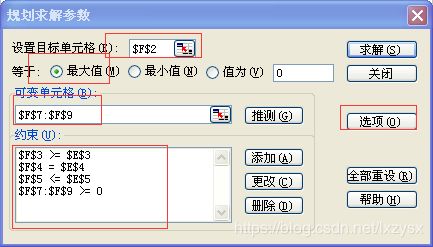
设置好之后,选择“选项”,进行配置,弄好之后就可以确定,然后在最初的界面选择“求解”
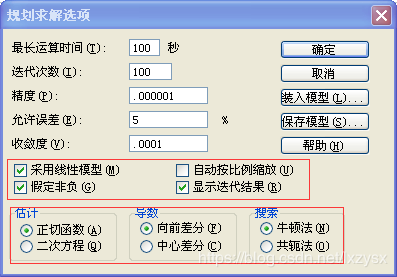
就会出现下面的报告
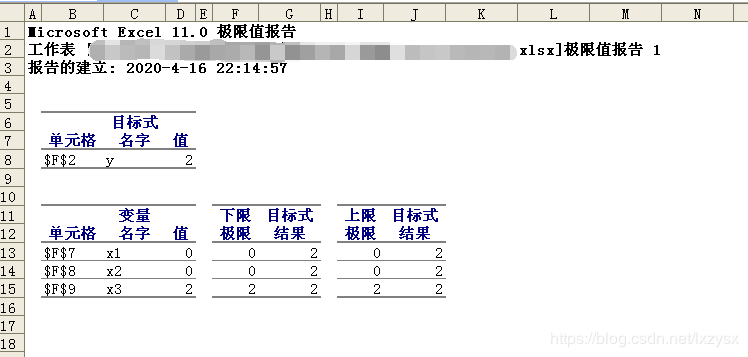

在这个运算结果里面可以看到最大值为2,x1=x2=0,x3=2
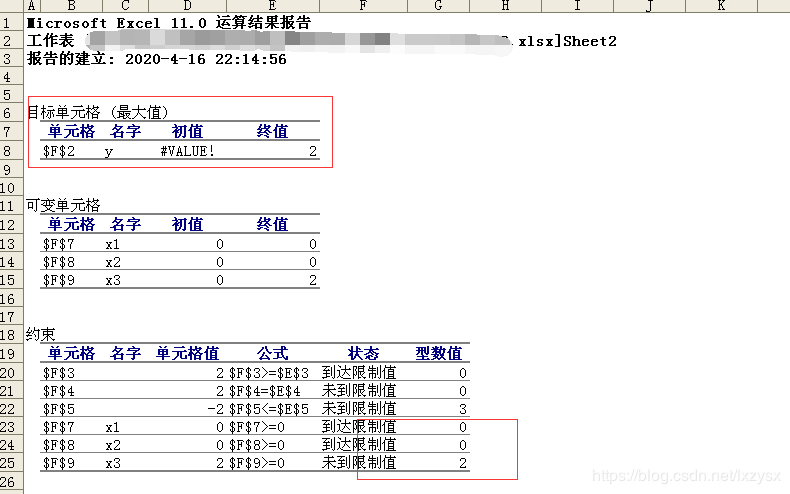
在最后的表格中也会看见x1x2x3的值,以及最优解为2
大M法
步骤




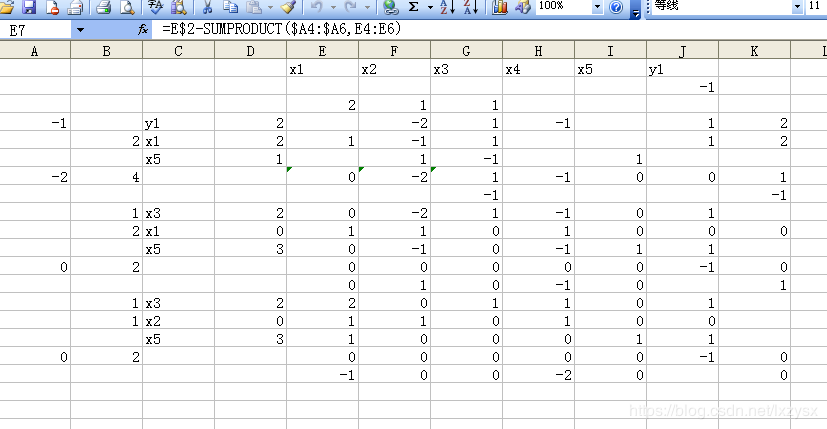
按照上述步骤,最终得到的如下:
得到最优解x1=x2=0,x3=2,最优值为2
Python编程
# encoding=utf-8
import numpy as np # python 矩阵操作lib
class Simplex():
def __init__(self):
self._A = ""
self._b = ""
self._c = ''
self._B = ''
self.row = 0
def solve(self):
A = []
b = []
c = []
self._A = np.array(A, dtype=float)
self._b = np.array(b, dtype=float)
self._c = np.array(c, dtype=float)
self._A = np.array([[0,2,-1],[0,1,-1]],dtype=float)
self._b = np.array([-2,1],dtype=float)
self._A = np.array([[1,-1,1]])# 等式约束系数self._A,3x1维列向量
self._b = np.array([2])# 等式约束系数self._b,1x1数值
self._c = np.array([2,1,1],dtype=float)
self._B = []
self.row = len(self._b)
self.var = len(self._c)
(x, obj) = self.Simplex(self._A, self._b, self._c)
self.pprint(x, obj, A)
def pprint(self, x, obj, A):
px = ['x_%d = %f' % (i + 1, x[i]) for i in range(len(x))]
print(','.join(px))
print('objective value is : %f' % obj)
print('------------------------------')
for i in range(len(A)):
print('%d-th line constraint value is : %f' % (i + 1, x.dot(A[i])))
def InitializeSimplex(self, A, b):
b_min, min_pos = (np.min(b), np.argmin(b)) # 得到最小bi
# 将bi全部转化成正数
if (b_min < 0):
for i in range(self.row):
if i != min_pos:
A[i] = A[i] - A[min_pos]
b[i] = b[i] - b[min_pos]
A[min_pos] = A[min_pos] * -1
b[min_pos] = b[min_pos] * -1
# 添加松弛变量
slacks = np.eye(self.row)
A = np.concatenate((A, slacks), axis=1)
c = np.concatenate((np.zeros(self.var), np.ones(self.row)), axis=0)
# 松弛变量全部加入基,初始解为b
new_B = [i + self.var for i in range(self.row)]
# 辅助方程的目标函数值
obj = np.sum(b)
c = c[new_B].reshape(1, -1).dot(A) - c
c = c[0]
# entering basis
e = np.argmax(c)
while c[e] > 0:
theta = []
for i in range(len(b)):
if A[i][e] > 0:
theta.append(b[i] / A[i][e])
else:
theta.append(float("inf"))
l = np.argmin(np.array(theta))
if theta[l] == float('inf'):
print('unbounded')
return False
(new_B, A, b, c, obj) = self._PIVOT(new_B, A, b, c, obj, l, e)
e = np.argmax(c)
for mb in new_B:
if mb >= self.var:
row = mb - self.var
i = 0
while A[row][i] == 0 and i < self.var:
i += 1
(new_B, A, b, c, obj) = self._PIVOT(new_B, A, b, c, obj, new_B.index(mb), i)
return (new_B, A[:, 0:self.var], b)
# 算法入口
def Simplex(self, A, b, c):
B = ''
(B, A, b) = self.InitializeSimplex(A, b)
# 函数目标值
obj = np.dot(c[B], b)
c = np.dot(c[B].reshape(1, -1), A) - c
c = c[0]
# entering basis
e = np.argmax(c)
# 找到最大的检验数,如果大于0,则目标函数可以优化
while c[e] > 0:
theta = []
for i in range(len(b)):
if A[i][e] > 0:
theta.append(b[i] / A[i][e])
else:
theta.append(float("inf"))
l = np.argmin(np.array(theta))
if theta[l] == float('inf'):
print("unbounded")
return False
(B, A, b, c, obj) = self._PIVOT(B, A, b, c, obj, l, e)
e = np.argmax(c)
x = self._CalculateX(B, A, b, c)
return (x, obj)
# 得到完整解
def _CalculateX(self, B, A, b, c):
x = np.zeros(self.var, dtype=float)
x[B] = b
return x
# 基变换
def _PIVOT(self, B, A, b, c, z, l, e):
# main element is a_le
# l represents leaving basis
# e represents entering basis
main_elem = A[l][e]
# scaling the l-th line
A[l] = A[l] / main_elem
b[l] = b[l] / main_elem
# change e-th column to unit array
for i in range(self.row):
if i != l:
b[i] = b[i] - A[i][e] * b[l]
A[i] = A[i] - A[i][e] * A[l]
# update objective value
z -= b[l] * c[e]
c = c - c[e] * A[l]
# change the basis
B[l] = e
return (B, A, b, c, z)
s = Simplex()
s.solve()
结果如下:

最终的结果为x1=x2=0,x3=2,最优值为2
Python包编程
#导入包
from scipy import optimize
import numpy as np
#确定c,A,b,Aeq,beq
c = np.array([2,1,1])
A = np.array([[0,2,-1],[0,1,-1]])
b = np.array([-2,1])
Aeq = np.array([[1,-1,1]])
beq = np.array([2])
#求解
res = optimize.linprog(-c,A,b,Aeq,beq,bounds=(x1,x2,x3))
print(res)
结果如下:
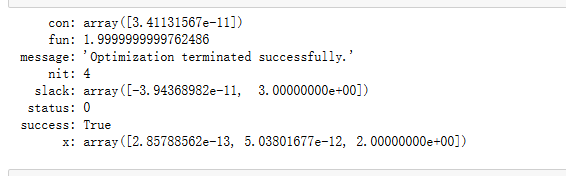
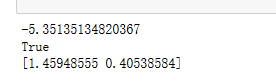
可以看出1.999999…趋近于2,所以最优值近似为2,x1=x2=0,x3=2
通过excel、python编程与python包编程发现,python包求解最为简便,而且通过python包scipy求解做出来的最后的结果值更加的精确
本次实验差不多从excel和python的角度来进行分析求最优解,通过这几个的对比发现,在还是python的包和单纯形法的excel规划求解来的比较的直接,因为都是他们弄好的直接调用包或者是使用工具就可以求出来。但是这些还是需要自己对原理的掌握,才能理解这些的含义,有利于我们更好的学习。
(2)非线性规划
非线性规划的拉格朗日乘子法的Excel,python编码和python包编码
在求取有约束条件的优化问题时,拉格朗日乘子法(LagrangeMultiplier) 和 KKT 条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉 格朗日乘子法去求取最优值;如果含有不等式约束,可以应用 KKT 条件去求取。
当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保 证是充分必要条件。KKT 条件是拉格朗日乘子法的泛化。
【非线性规划问题一般是有约束条件的寻优问题,约束条件可以分成两类:等式约束与不等式约束;也可以将拉格朗日乘子法受约束优化问题转化为无约束优化(与KKT条件)】
等式约束的拉格朗日乘子法
不等式约束的拉格朗日乘子法
无约束的拉格朗日乘子法(KKT条件下)
首先将原目标公式和等式不等式合为一个公式
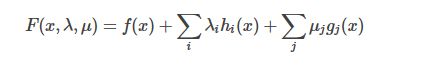

在进行下面的操作的时候,我们所用到的实例如下:
手推法
python包编程
from scipy.optimize import minimize
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
#目标函数:
def func(args):
fun = lambda x: 2*x[0]**2-2*x[0]*x[1]+2*x[1]**2-6*x[0]
return fun
#约束条件,包括等式约束和不等式约束
def con(args):
cons = ({'type': 'ineq', 'fun': lambda x: 6-3*x[0]-4*x[1]}, #这里的ineq是指大于等于0
{'type': 'ineq', 'fun': lambda x: x[0]-4*x[1]+2})
return cons
if __name__ == "__main__":
args = ()
args1 = ()
cons = con(args1)
x0 = np.array((1.0, 2.0)) #设置初始值,初始值的设置很重要,很容易收敛到另外的极值点中,建议多试几个值
#求解#
res = minimize(func(args), x0, method='SLSQP', constraints=cons)
#####
print(res.fun)
print(res.success)
print(res.x)
参考文献
1.单纯形法
2.用Excel演示大M单纯形法
3.Python数学模型——线性规划求解(一)
4.非线性优化-拉格朗日乘子法
5.拉格朗日乘子法原理分析
6.python 非线性规划(scipy.optimize.minimize)
7.利用Python求解带约束的最优化问题