机器学习之SVM(Hinge Loss+Kernel Trick)原理推导与解析
支持向量机(Support Vector Machine, SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面。
SVM使用铰链损失函数(hinge loss)计算经验风险(empirical risk)并在求解系统中加入了正则化项以优化结构风险(structural risk),是一个具有稀疏性和稳健性的分类器。SVM可以通过核方法(kernel method)进行非线性分类,是常见的核学习(kernel learning)方法之一 。
因此,hinge loss+kernel trick就是Support Vector Machine。
本文借助了李宏毅机器学习笔记,主要是用通俗易懂的语言来推导出hinge loss和kernel trick。
目录
- 1.引入Hinge loss
- 1.ideal loss
- 2.Square loss
- 3.Sigmoid+Square loss
- 4.Sigmoid+Cross entropy
- 5. Hinge loss
- 2.线性SVM
- 1.Step1:定义Function
- 2. Step2:定义loss function。
- 3.线性SVM的另外一种表述
- 3.kernel function的引入
- 1. function set
- 2.损失函数+训练
- 3.kernel trick
- 4.Radial Basis Function Kernel
- 5.Sigmoid Kernel
1.引入Hinge loss
在下面的问题中loss代表每一个样本的损失,Loss代表总的损失。
首先我们需要回顾一下前面所学的二分类问题:假设有一批样本, x 1 x^1 x1, x 2 x^2 x2, x 3 x^3 x3,…, x n x^n xn,对应的label分别是: y 1 ^ y\hat{1} y1^, y 2 ^ y\hat{2} y2^, y 3 ^ y\hat{3} y3^,…, y n ^ y\hat{n} yn^, y i ^ y\hat{i} yi^(i=1,2,…,n)有两个取值,-1和1,则Binary Classfication:
if f(x)>0,output=1,属于一个class
if(f(x)<0),output=-1,属于另一个class
在二分类问题中loss function的定义有很多种,其中最理想的loss function定义为:
![]()
即若分类正确loss=0,否则loss等于1,那么在这里Loss可以理解分类器在训练集上犯错误的次数。but如果Loss这样定义,是不能求微分的,所以我们换了一种方式,即:
![]()
我们以 y n ^ f ( x ) y\hat{n}f(x) yn^f(x)作为横轴,loss作为纵轴,从二分类的定义来看,当f(x)>0时,output=1,即 y n ^ = 1 y\hat{n}=1 yn^=1时,f(x)是越大越好的,同理,当 y n ^ = − 1 y\hat{n}=-1 yn^=−1时,f(x)是越小越好。 因此,当 y n ^ f ( x ) y\hat{n}f(x) yn^f(x)越大时,loss会越小。 这是我们判断一个loss function好坏的标准。
针对上面这个表达式,我们有以下几种情况可以讨论(加上ideal loss):
1.ideal loss
定义:![]()
这个loss比较好理解,可以直接画出图像:

如图中黑线所示,当 y n ^ f ( x ) y\hat{n}f(x) yn^f(x)>0时,表面分类正确,loss=0,否则等于1。从其图像我们也可以看出,loss是不能进行Gradient Descent的。
2.Square loss
Square loss是用使用MSE来衡量误差,若output=1时,f(x)应该尽量接近1而当output=-1时,f(x)又应该尽量接近于-1,只有这样Square loss才能最小。因此我们可以定义 l ( f ( x n , y n ^ ) ) l(f(x^{n},y\hat{n})) l(f(xn,yn^)):

可以看出,该表达式是满足MSE定义的,我们画出 ( x − 1 ) ² (x-1)² (x−1)²的图像,如下所图红线示:
前面我们讨论过,当 y n ^ f ( x ) y\hat{n}f(x) yn^f(x)越大时,loss应当会越小。 但是Square loss显然是不符合情况的,这里也可以进一步解释前面我们为什么说不能用Square loss来作为损失函数。
3.Sigmoid+Square loss
![]()
Sigmoid函数值域介于01之间,因此当output=1时, σ ( f ( x n ) ) \sigma (f(x^{n})) σ(f(xn))应该尽量接近1,而当output=-1时, σ ( f ( x n ) ) \sigma (f(x^{n})) σ(f(xn))又应该接近于0,因为其本质还是Square loss,只不过把输出映射到了01之间,因此,我们可以定义 l ( f ( x n , y n ^ ) ) : l(f(x^{n},y\hat{n})): l(f(xn,yn^)):

同样画出图像:
从目前来看,该损失函数好像挺合理的,但仔细一想又是不对的。该函数的渐近线是y=1,越往左loss是越大的,但是其斜率是越来越小的。在Gradient Descent中,如果一个位置的loss太大那么它应该更加快速的下降以找到最优解,但是上述函数不符合要求,loss越大下降反而越慢,属于典型的“没有回报,不想努力。”
4.Sigmoid+Cross entropy
在逻辑回归中我们最终选择了交叉熵的形式,这里定义 l ( f ( x n , y n ^ ) ) : l(f(x^{n},y\hat{n})): l(f(xn,yn^)):

画出图像:
可以看出,从左到右符合下降的趋势,并且相较与Sigmoid+Square loss,Sigmoid+Cross entropy的loss越大,其梯度越大,情况符合“有回报有努力。”
因此最终看来,Sigmoid+Cross entropy似乎是比较好的选择了。
5. Hinge loss
l ( f ( x n , y n ^ ) ) l(f(x^{n},y\hat{n})) l(f(xn,yn^))定义为:

从表达式可以看出,当 y n ^ = 1 y\hat{n}=1 yn^=1时, f ( x n ) > 1 f(x^{n})>1 f(xn)>1则loss=0;当 y n ^ = − 1 y\hat{n}=-1 yn^=−1时, f ( x n ) < − 1 f(x^{n})<-1 f(xn)<−1则loss=0。
同样画出图像:

比较Hinge loss和Sigmoid+Cross entropy,比如说我们把黑点从1移动到2,可以发现Sigmoid+Cross entropy其实是可以做得更好的,而Hinge loss只要是 y n ^ f ( x ) y\hat{n}f(x) yn^f(x)大于它的阈值,无论怎么调整loss都不会变。但是当我们有outlier也就是异常值的时候,Hinge loss会给出比Cross entropy更好的结果。 这个后面再解释。
2.线性SVM
Linear SVM与逻辑回归相比,只是loss function有点不同。
1.Step1:定义Function

Function就是线性模型的定义方式,不过我们把 ( w , b ) T (w,b)^T (w,b)T定义为新的w, ( x , 1 ) T (x,1)^T (x,1)T定义为新的x,那么最后 f ( x ) = w T x f(x)=w^Tx f(x)=wTx。
2. Step2:定义loss function。

Linear SVM的loss function就是Hinge loss+regularization item,也就是加上一个正则化项,二者都是convex function也就是凸函数,相加之后仍为凸函数。
因此线性SVM与逻辑回归相比就是loss function不同,如果使用Hinge loss就是线性SVM,使用Cross entropy就是逻辑回归。
Step3:Gradient Descent
求微分时忽略正则化项。

这里只需要注意Hinge loss对 f ( x n ) f(x^n) f(xn)求导时,需要分类讨论。
3.线性SVM的另外一种表述

我们把Hinge loss加上一个正则化项,并令Hinge loss= ε n \varepsilon ^{n} εn,对于红框框里面的内容,上下两部分是不一样的,上面的 ε n \varepsilon ^{n} εn一定是max里面的其中一个值,而下面则表示一个范围。但是当我们最小化L(f)时,二者就是等价的。 这点其实点不好理解,李宏毅老师当初讲的时候我也没太明白,不过最后还是搞明白了。
不妨可以这样理解:最小化L(f),其实就是找到一个最小的 ε n \varepsilon ^{n} εn,而:

那么在这里, ε n \varepsilon ^{n} εn最小其实就是 m a x ( 0 , 1 − y n ^ f ( x ) ) max(0,1-y\hat{n}f(x)) max(0,1−yn^f(x)),所以二者等价。
啊啊啊再让我们回到最开始讲的Hinge loss,

在上面这张图里面,Hinge loss的margin是1,而在线性SVM中,我们有:
y n ^ f ( x ) > = 1 − ε n y\hat{n}f(x)>=1-\varepsilon ^{n} yn^f(x)>=1−εn,在这里margin被放宽了,我们称 ε n \varepsilon ^{n} εn为松弛因子。也就是Hinge loss与横轴的交点会向左移动。
3.kernel function的引入

前面我们用梯度下降求微分得到上面这个式子,其中 c n ( w ) c^n(w) cn(w)就是Hinge loss对 f ( x n ) f(x^n) f(xn)的微分,也就是那个分段函数。

这段很重要,一定要注意理解!!!
注意前面我们把 ( w , b ) T (w,b)^T (w,b)T定义为了新的w,也就是说w包含了所有参数。回顾一下梯度下降法,我们求得l(f)对w的微分然后求和就是Total loss对w的微分,对x来说上标表示样本序号,下标表示特征序号,那么假设有k个特征,也就是k维,w也就从w1,w2,…,wk。对其中任意一个样本 x n x^n xn,根据最后微分的结果表达式,我们都可以求得一组w也就是包含k个w的向量。然后对每一个样本都求出这么一个向量,我们再加起来,乘以一个负的learning rate也就是 − η -\eta −η,最后与上一轮的w相加,即得到下一轮更新后的w。
假设我们把 c n ( w ) c^n(w) cn(w)看做一个权重系数,从上面这段话我们可以看出来,每次更新w时我们都对原来的w加上了一个 x n x^n xn的线性组合!!! 也就是求和那一项。
c n ( w ) c^n(w) cn(w)是损失函数 l ( f ( x n ) , y n ^ ) l(f(x^n),y\hat{n}) l(f(xn),yn^)对 f ( x n ) f(x^n) f(xn)的导数。假设我们的损失函数采用Hinge loss, c n ( w ) c^n(w) cn(w)往往就是0。因为Hinge loss:

从上面表达式我们可以看出,当 l ( f ( x n ) , y n ^ ) l(f(x^n),y\hat{n}) l(f(xn),yn^)为0时候, c n ( w ) c^n(w) cn(w)就是0。不妨定义:
也就是说w是所有data points的一个线性组合,这个我们在上面已经说明过了。既然这个权重 c n ( w ) c^n(w) cn(w)也就是上面表达式里面的 a n ∗ a_{n}^{*} an∗是有可能为0的,也就是说,不是所有的所有的点都会加到这个新的向量里面去,也即是说 a n ∗ a_{n}^{*} an∗可能会是稀疏的,因为它可能有很多0嘛。
有点晕,再理一理:

从上面这个表达式可以看出来,可能有的 x n x^n xn我们代入 f ( x n ) f(x^n) f(xn)后呢,可能使得1+ f ( x n ) f(x^n) f(xn) or 1 − f ( x n ) 1-f(x^n) 1−f(xn)小于0,那么此时的Hinge loss取最大值,就是0,那么再求导得到的 c n ( w ) c^n(w) cn(w)也就是上面表达式里面的 a n ∗ a_{n}^{*} an∗,也就是等于0的,但是不是所有的 x n x^n xn代入都会导致其最终结果是0,那么这些使得最终结果不为0的那些 x n x^n xn我们就称之为Support Vector,即支持向量。
这一模型有什么好处呢?答案是具有较强的鲁棒性。 不是支持向量的数据点,就算去掉也不会对结果有影响,因为它的结果是0嘛,所以对更新后的w是没有一点影响的,而异常点只要不是支持向量,就不会对结果有影响。反观logistic regression(用cross entropy作损失函数),它在更新参数时的 c n ( w ) c^n(w) cn(w)永远不会为0,权重就不是稀疏的,所以每个data都对结果有影响。
然后引入核函数:
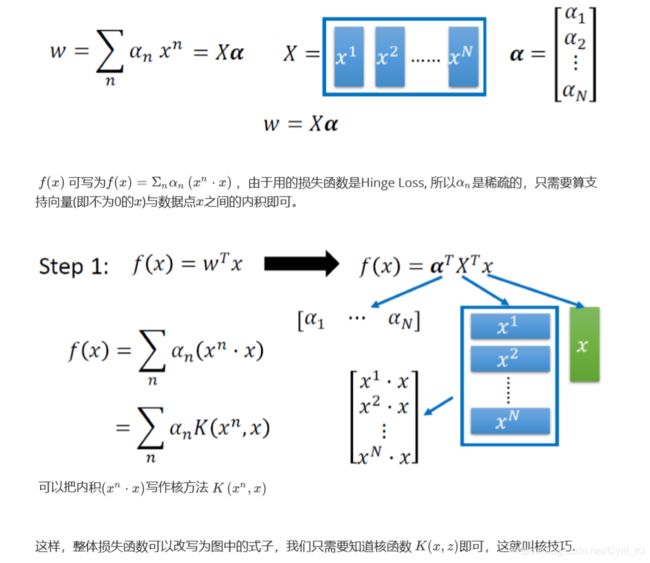
上面的 a n a_{n} an就是把每一个样本数据代入然后对w求导数得到的,把所有的这些导数组成一个向量,我们命名为α,需要知道,α里面是有些数据是0,这个上面也讲到过。又令X为所有样本组成向量的转置,于是更新后的w就可表示成: w = X α w=Xα w=Xα。
而最开始我们定义的函数集为:

因此最终:
![]()
其中 x x x是测试集里面的样本。

因此 f ( x ) f(x) f(x)就可以写成上面这个式子,其中核函数 K ( x n , x ) K(x^n,x) K(xn,x)表示对括号里面那个向量求inner product也就是内积。
1. function set
2.损失函数+训练

其实学到这里,感觉有一点晕了,就很多乱七八糟的向量相乘,要么是不知道这个向量表示什么,要么就是不知道这个向量的维度是什么,索性我就找张纸重新推一推,如下所示:
算是思路重新理清了。
因此最小化loss function其实就是找到一组α使得loss function最小,因为内积那部分是已知的。
3.kernel trick
为什么使用核技巧?
从前面的学习中我们可以看出来,SVM构建的是一个线性的决策边界,从而把数据集分到各自的类中,如果数据集是一个非线性的,直接使用SVM,得不到一个理想的结果,那么使用线性分类器求解非线性分类问题,需要特殊的处理:
- 首先,使用一个变换将原空间的数据映射到新空间中
- 然后,在新空间中使用线性分类器求解
假设每一个样本都是二维的,我们想要把它映射到三维(可能映射到三维就可以使用线性分解器求解了),就需要进行feature transformation也就是特征转换,如下所示:

ϕ ( x ) \phi (x) ϕ(x)是进行特征转换后的x,假设我们要计算 K ( x , z ) K(x,z) K(x,z),这其中 x , z x,z x,z都是映射到高维的样本,然后一系列推导我们发现:
样本映射到高维后再进行inner product等于没映射前进行inner product后再平方, 这一发现可以使我们简化运算。
假设x,z不是2维,而是高维,想要将它投影到更高的一个空间,就会考虑所有点两两之间的关系:

我们此时要求映射到高维后的 x 和 z x和z x和z的核函数,就可以先在低维求inner product然后再平方。因为要考虑所有所有点两两之间的关系,所以映射后的维度是 C k 2 C_{k}^{2} Ck2维,假设k很大,则高维的维度已经特别大了,因此我们至少简化了 C k 2 − k C_{k}^{2}-k Ck2−k次运算。
4.Radial Basis Function Kernel
RBF kernel即径向基核函数。
这个时候定义核函数为:
![]()
即 x 和 z x和z x和z距离乘上-0.5再取exp函数。这个函数是衡量 x 和 z x和z x和z的相似度,若二者很相似,exp后就越靠近1。(完全一致就是1,完全不一致就是0)。按照上面的思路,我们依旧把 K ( x , z ) K(x,z) K(x,z)化成两个映射到高维后的向量的inner product,即:
![]()
ϕ ( x ) \phi (x) ϕ(x)是映射函数。

对RBF核函数变形,可以看出它有无穷多项,那么映射之后也是无穷多项,这根本没法算inner product,但是我们不需要算,我们只需要算距离乘上-0.5再取exp就行了。
5.Sigmoid Kernel

这里把Sigmoid Kernel看成了一个单层的神经网络,神经元个数就是support vector的个数(其他为0,不用考虑),我们测试的x要与训练集中每一个x求内积,激活函数这里就是tanh函数了,最后还要乘上系数α,因此这个单层的神经网络的结构其实是很好理解的。
综上所述,我们可以直接设计 K ( x , z ) K(x,z) K(x,z)而不是考虑映射到高维后的 ϕ ( x ) \phi (x) ϕ(x), ϕ ( z ) \phi (z) ϕ(z),因为当x是像序列这样的结构化对象时,是很难设计高维的,核方法的好处就是可以直接去设计核函数不用考虑x和z的特征长什么样。