【纪中2020.2.3日】模拟赛题解
目录:
T1:sort
T2:sum
T3:count
T4:ranking
又是一届快乐的%你赛……
那么,我们从T1开始……
T1:Sort
题目描述
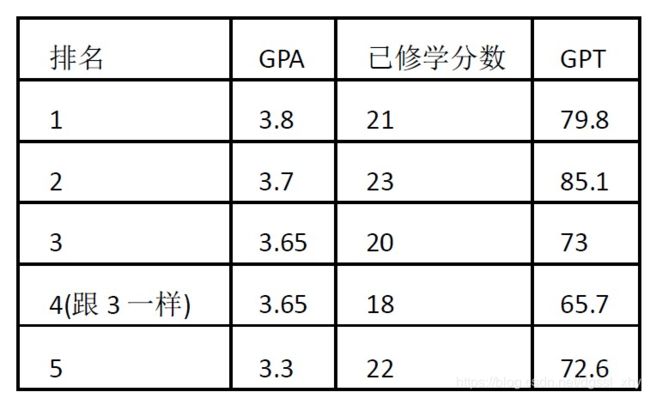
小x和小y是好朋友。小y的成绩很差,以至于 GPA(平均绩点)在系内倒数。系内一共有 N 位同学,每位同学有自己的 GPA,以及已修学分数,定义 GPT = GPA ×已修学分数。小x为了帮助小y提高成绩,给小y提了一个要求:新学期的 GPA 要超过系内排名第 K 位的同学。 为了帮助理解,给出一个例子:
现在给出系里面每位同学的 GPT(只有一位小数),以及他们的已修学分。你需要帮助小y把排名 第 K 位的同学的 GPA 求出来。
输入
第 1 行2 个整数 N, K。
第 2- (N + 1) 行,每行 1 个非负实数和 1 个整数,分别表示 GPT 和已 修学分数。
注意:所有同学的学分都在 [1, 250] 的范围。
输出
第 1 行1 个实数,表示排名第 K 同学的 GPA,保留 2 位小数输出。
样例输入
5 3
73 20
79.8 21
72.6 22
85.1 23
65.7 18
样例输出
3.65
分析:
这题是真的水。我们要求的GPA就是GTP除以已修学分得出的。开个结构体存存就好了。
CODE:
#includeT2:Sum
题目描述
小x有很多糖果,分成了 N 堆,排成一列。小x说,如果小y能迅速求出第 L 堆到第 R 堆一 共有多少糖果,就把这些糖果都给他。
现在给出每堆糖果的数量,以及每次询问的 L 和 R,你需要帮助小y,把每次询问的结果求出来。 注意,你不需要考虑糖果被小y取走的情况。
输入
第 1 行2 个整数 N, M, 分别表示堆数和询问数量。
第 2 行N 个整数 Ai,表示第 i 堆糖果的数 量。
第 3- (M + 2) 行,每行 2 个整数 Li, Ri,表示第 i 个询问是 [Li, Ri]。
输出
M 行,对于每个询问,输出对应的和。
样例输入
5 5
1 2 3 4 5
1 5
2 4
3 3
1 3
3 5
样例输出
15
9
3
6
12
分析:
我们先预处理前缀和,然后每个区间内的和其实就是:sum[终点]-sum[起始-1]。
CODE:
#includeT3:Count
题目描述
小x开发了一个奇怪的游戏,这个游戏的是这样的:一个长方形,被分成 N 行 M 列的格子,第 i 行第 j 列的格子记为 (i, j),就是说,左上角的格子是 (1, 1),右下角的格子是 (N, M)。开始的时候,小y在 (1, 1),他需要走到 (N, M)。每一步,小y可以走到正右方或者正下方的一个格子。具体地说,如小y现在在 (x, y),那么他可以走到 (x, y + 1) 或 (x + 1, y)。当然,小y不能走出离开这个长方形。
每个格子有积分,用一个 1~10 的整数表示。经过这个格子,就会获取这个格子的积分(起点和终 点的积分也计算)。通过的方法是:到达 (N, M) 的时候,积分恰好为 P 。
现在给出这个长方形每个格子的积分,你需要帮助小y,求出从起点走到终点,积分为 P 的线路有多少条。
输入
第 1 行3 个整数 N, M, P 。
接下来 N 行,每行 M 个整数 Aij ,表示格子 (i, j) 的积分。
输出
1 行1 个整数,表示积分为 P 线路的数量。
因为数值太大,你只需要输出结果除以 (10^9 + 7) 的 余数。
样例输入
3 3 9
2 2 1
2 2 2
1 2 2
样例输出
2
分析:
这道题本来想用搜索,但搜索会超时;
于是就需要用DP(正解)来做。
可得动态能量转移方程:
(三维数组)
f[i][j][k]+=f[i-1][j][k-a[i][j]]+f[i][j-1][k-a[i][j]];
CODE:
#includeT4:Ranking
题目描述
小x有n个小姊妹(根据典故,我们假设n≤3000)。他每天都喜欢按不同标准给小姊妹们排(da)序(fen)。今天,他突然对小姊妹们的名字产生了兴趣。他觉得小姊妹的魅力和她们的名字有密切联系,于是他觉得所有有相似的名字的小姊妹必须排在一起。
相似是指,名字的开头一个或若干个连续字母相同。
于是,小x定下了如下规则:
在任何以同样的字母序列开头的名字之间,所有名字开头必须是同样的字母序列。
比如,像MARTHA和MARY这两个名字,它们都以MAR开头,所以像MARCO或MARVIN这样的名字可以插入这两个名字中间,而像MAY这样的就不行。
显然,按字典序排序是一个合法的排序方案,但它不是唯一的方案。你的任务就是计算出所有合法的方案数。考虑到答案可能很大,输出答案 mod 1 000 000 007。
输入
第一行一个整数n,小x的小姊妹个数。
第2~n+1行,每行一个字符串,代表这个小姊妹的名字。
输出
一行一个整数,合法的方案数。
样例输入
3
IVO
JASNA
JOSIPA
样例输出
4
分析:
jz函数是求阶乘的函数。
dg函数是字符串处理的:先判断是否合法,再记录位置&&标记;
再根据标记去匹配,方案数++;mod操作也在dg函数内完成。
CODE:
#include