博弈论-SG函数（4024. 【佛山市选2015】石子游戏）

题目描述

Description
Alice 和 Bob 总喜欢聚在一起玩游戏（T_T），今天他（她）们玩的是一款新型的取石子游戏。游戏一开始有N堆石子，Alice 和 Bob 轮流取出石子。在每次操作中，游戏者必须选择其中的一堆石子，并作出下列的其中一种操作：
(1)移去整堆石子
(2)假设石子堆中有X颗石子，取出Y颗石子，其中1<=Y
游戏结束的条件是：取出最后一颗石子的人胜出。众所周知，Alice和Bob都是绝顶聪明的，假设他们在游戏中都采取最优的策略，问最后谁会胜出游戏呢？

Alice先取。

Input
第一行包含一个整数T，表示测试数据的组数。
接下来T组测试数据，在每组数据中，第一行包含一个整数N，表示有多少堆石子。第二行N个正整数，分别表示每堆有多少颗石子。
Output
每组测试数据输出一行，表示获胜者的名字（Alice 或者 Bob）。

Sample Input
3
3
3 5 6
4
2 3 6 9
5
3 2 1 1000000 999999
Sample Output
Alice
Bob
Alice

Data Constraint
20%的数据，N<=5，每堆石子数量少于10
100%的数据，T<=100，N<=100，每堆石子数量不大于1,000,000

20%

暴力

100%

没错这就是传说中的博弈问题
以下内容请感性理解

别问为什么因为我也不会证

Nim游戏

从头开始讲吧

有这样一个问题：

假设现在有n堆石子，每堆石子有若干个。
有两个人轮流取石子，每人每次可以取其中一堆的若干个石子，取走最后一个石子的人获胜（假设两个人都按照最优策略取），问谁会获胜？

---

定义P-position状态为先手必败，N-position状态为先手必胜

若当前有一个状态
①此状态为空（terminal position），即无法进行任何移动，那么显然是P
②此状态可以走到一个P，则其为N，因为先手可以给对方留下一个必败态
③此状态走不到 任何一个 P，则其为P，因为留给对方的都是必胜态

这个性质与博弈中的许多东西都有关

---

那么把这个定义放到Nim游戏上
设当前状态为(a1,a2…an)

①(0,0…0)=P
②(a1,a2…an)----->P =N
③(a1,a2…an)-×->P =P

于是可以Dp或记忆化搜索
但是当n一大时，时间复杂度将会是$O(a1\ast a2\ast ...\ast an)$
会炸

结论

Nim游戏有一个神奇的性质：
设一个状态为(a1,a2…an)，则当
a1^a2…^an=0 时则为P，否则为N （^为异或运算）
奥妙重重

证明

如果该结论成立，那么一定满足上面所说的三个性质
证明：

①为空，即为(0,0…0)时： 0⁰…^0=0 为P

②a1^a2…^an≠0，则设其为k
那么一定有一个数有k二进制下的最高位（不然k的最高位怎么来的）
所以把它^=k即可
③a1^a2…^an=0
显然无论怎么搞结果都不为0

感性理解

有向图游戏

又有一个问题：

给出一个有向无环图（不一定是树），上面有一个点，双方轮流操作，每次把这个点沿着有向边移动，最后不能移动者输。问谁会获胜？

比如这样（方向都是从上往下懒得画）：

还是考虑上面的三条性质：
①不能走时为P

②能走到P的为N

③走不到P的为P

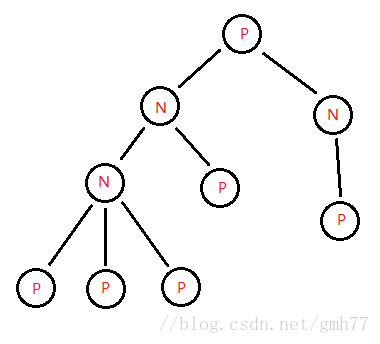
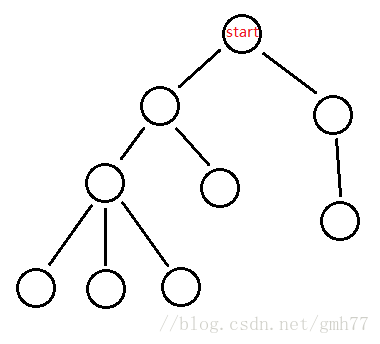
于是可以在$O(n)$的时间里处理出所有的结果，然后直接回答(滑稽)

有向图游戏2

但是这样做只能解决只有一个点的情况，
如果有多个点有GG了

给出一个有向无环图，上面有N个点，双方轮流操作，每次把这N个点沿着有向边移动，最后不能移动者输。问谁会获胜？

如果有多个点的话，双方都可以轮流操作不同的点

所以有了这个神奇的东西——SG函数

SG函数

定义mex(minimal excludant)函数，表示在一个集合内最小未出现的自然数
例如
mex{1,2,3}=0，mex{0,2,3}=1，mex{0,1,3,4}=2

则定义SG(i)表示状态为i时的SG值，有
$S{G}_i=mex\{S{G}_j\}$（i能到j）
*也有可能从一个状态走到一个局面（比如把一棵树拆开成森林，且SG表示的是树的），那么$S{G}_i=mex\{S{G}_{j1}xorS{G}_{j2}xorS{G}_{j3}xor...\}$

至于SG是什么……实际上意义不明
大概就是用数字来表示N/P状态

---

那么上面图的SG值对应如下：

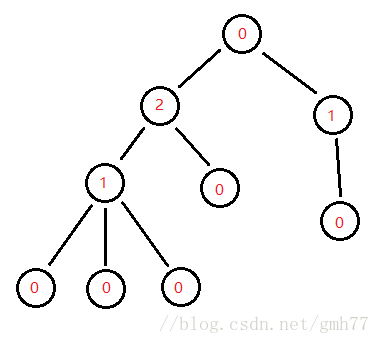
到这里应该可以看出来了，
当SG(i)>0时表示这是个必胜态，SG(i)=0时是必败态。

然而这跟上面的问题似乎没有半毛钱关系

Nim游戏+有向图游戏+SG函数=博弈

通过观察可以发现，SG(i)=k表示i能走向SG为0~k-1之间的数
换句话说，就是每次操作一个点时SG值可以减去1~k，最后为0时停止

欸这不就是Nim游戏吗
重申一遍Nim游戏：每次选择一堆石子，拿走其1~石子个数的石子

所以实际上SG为i的点，其操作方式等同与Nim中的一堆个数为i的石子！
于是问题转化为了Nim游戏，而Nim游戏的判定方式上面写了

所以当SG(a1)^SG(a2)…^SG(an)=0时为先手必败，否则为先手必胜
每个局面的SG值就是SG(a1)^SG(a2)…^SG(an)

所以这类博弈问题的一般套路：
初始—找状态之间的关系—>有向图游戏—求SG函数—>Nim游戏—求解—>AC

还是感性理解

上面的问题

现在就简单了，直接上SG
$S{G}_i=mex(\{S{G}_j\}{}_{gcd(i,j)=1}\bigcup \{0\})$
这里的i表示石子还剩i个
因为gcd(i,i-j)=1，所以gcd(i,j)=1 (自己理解)，并且可以直接取完(0)，所以是上面那样

剩下的就直接copy吧

若i是质数，那么对于小于i的所有正整数都可以被取到，那么SGi则应为之前出现 过的所有SG值中最大者+1，我们不难发现质数们的SG值是递增的。
若i是一个合数，那么i肯定存在某个因子为前面出现过的质数，于是SGi 最多为该 质因子的SG值。又有质数们的SG值是递增的，那么 SGi 就应为最小质因子的SG值了。
我们发现合数必定不能产生新的SG值，它必定为其某个质因子的SG值。 于是第k个质数的SG值就是k+1了。
类似线性筛质数的原理，我们可以线性筛出SG值了。

code

正常版

#include 
#include 
#include 
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define len 1000000
using namespace std;

int g[len+1];
int p[len+1];
int i,j,k,l,n,t;

int main()
{
	g[0]=0,g[1]=1;
	k=1;
	
	l=0;
	fo(i,2,len)
	{
		if (!g[i])
		p[++l]=i,g[i]=++k;
		
		fo(j,1,l)
		if (i*p[j]<=len)
		{
			g[i*p[j]]=g[p[j]];
			
			if (!(i%p[j]))
			break;
		}
		else
		break;
	}
	
	scanf("%d",&t);
	for (;t;t--)
	{
		scanf("%d",&n),k=0;
		
		fo(i,1,n)
		{
			scanf("%d",&j);
			k^=g[j];
		}
		
		if (k)
		printf("Alice\n");
		else
		printf("Bob\n");
	}
	
	return 0;
}

压缩版

话说c++的压代码能力真是强

#include 

int g[1000001]={0,1},p[1000001],i,j,k=1,l,n,t;

int main()
{
	for (i=2; i<=1000000; i++)
	{
		if (!g[i]) p[++l]=i,g[i]=++k;
		for (j=1; j<=l && i*p[j]<=1000000 && (j==1 || i%p[j-1]); g[i*p[j]]=g[p[j]],j++);
	}
	
	for (scanf("%d",&t);t;t--)
	{
		for (k=0,scanf("%d",&n);n;n--,k^=g[scanf("%d",&j),j]);
		printf(k?"Alice\n":"Bob\n");
	}
}

后记

SG真奇♂妙

参考资料

https://blog.csdn.net/summer__show_/article/details/70185470
https://blog.csdn.net/strangedbly/article/details/51137432