为什么做机器学习的很少使用假设检验？ （转载）

本文转载，非原创，用于学习，在这之中也必有疏漏未加标注者，如有侵权请与博主联系。

原文地址：https://www.cnblogs.com/devilmaycry812839668/p/10136063.html

 

原文地址：

https://www.zhihu.com/question/55420602

最近在学习机器学习方面的内容，如题所说，对于为什么机器学习中不使用假设检验十分不解，在网上搜寻了一些资料最后发现还是知乎上的这个帖子回答的比较靠谱，也比较全面，其实个人感觉机器学习很少用到统计模型自然不太用假设检验，即使用到了统计模型在计算机学科中关注的是是否可以work，对于结果是否能否定最初假设也不是很关心的，当然这只是个人观点，下面给出知乎帖子的原文内容。

 

以下是原文内容：

====================================================================

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

作者：郭昊天
链接：https://www.zhihu.com/question/55420602/answer/394490229
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 

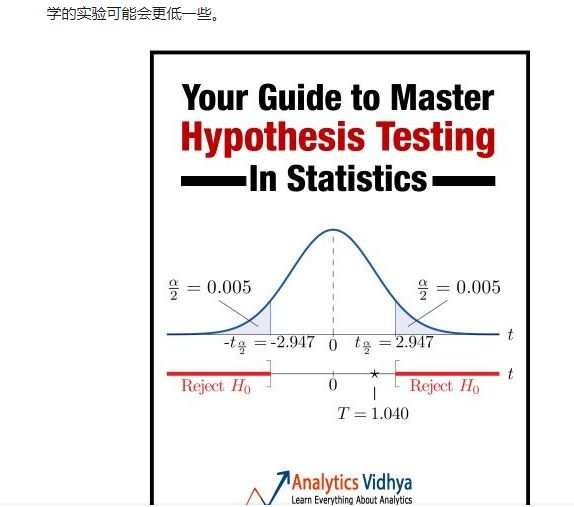
假设检验只是个统计推断的方法。目的是根据观测数据判断数据所属的群体的统计特征——我们人为地测试一些假说，看看是不是符合。

并不是说只有t-test，Z-test等才叫假设检验。经典的test，比如什么t-test，F-test，Chi-square test都要求样本先验地符合正态分布，但是假设检验的方法本身并不要求这一点。

需要注意的是，检验统计量也不是唯一的，实际上你可以发明出来无穷多种检验统计量，只要是一个可计算的函数即可。而对于一个假设检验，往往有很多种检验统计量可用，不同的检验统计量也必然有不同的适用范围。

反过来说，虽然常见的这些test平时都还挺好用的，但是随着数据的积累，上述这些test其实都会逐个失效——低维数据可能还可幸免，高维空间里能有多少数据符合正态分布啊。随着知识的积累，你完全可以给出更好的检验统计量，也就是提高统计功效（statistical power），统计学上有很多更普适的方法（然并卵，做实验的没什么人知道）。

高维的大量数据，直接用分布之间的各种距离函数（divergence）是一个更好的选择。根据Neyman–Pearson lemma，似然函数（likelihood function）肯定是最好的，虽然大多数情况下没法算。

推进一点就会细思恐极——如果知识有误，做出错误的assumption，那么假设判断的结果就是错的，而我们做实验正是因为对研究对象不了解，又怎么能保证做出合理的assumption呢？很多实验科学家并不注意或者根本不知道这个事情，就会滥用p-value，导致实验不能重复、或者换个test就不work的情况。

 

 

 

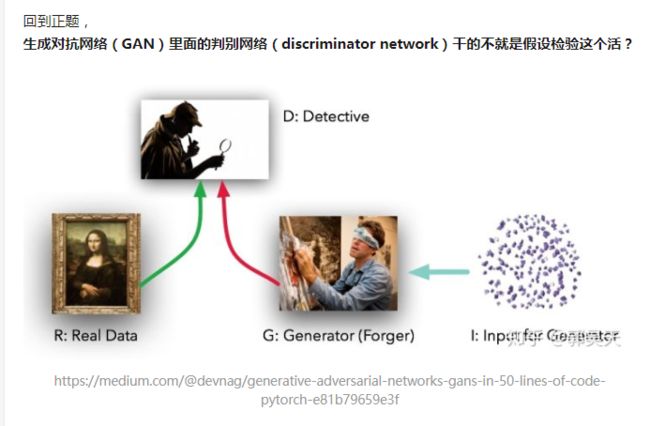
零假设：生成样本（比如上图中的右图）和原样本（上图中间的梵高原画）符合一个群体

对立假设：生成样本和原样本不符合一个群体

检验统计量：JS divergence 或者其他的描述分布之间差异的函数，比如WGAN用的EM divergence

要说和平常用的检测唯一的一点差别，就是由于我们完全没办法做第3步——梵高的画的特征怎么定量描述，更别提怎么算divergence了，所以这个假设检验的第3-7步都是在一个封装的判别网络这个黑盒子里面，而这个黑盒子里面的所有参数都是练出来的。

 

 

 

更进一步的，我们机器学习所有用于预测的流程，基本上等同于一个假设检验的过程。以图像分类（image classification）为例吧：

1. 你拍了一张照片，但是你不知道怎么标记（label）这张照片

 

2. 你列出了一些可能的label。我们可以简单一点，要求这个图像不是猫就是狗。

3. 你找到了一个已经训练好的系统，比如说叫CatOrDogNet吧。并且先验认定所有的猫都有一致的图像特征，狗亦如是，每张照片都是统计独立的。

4. 然后把你的图像扔给CatOrDogNet，他会根据每张照片，也就是观测数据，判断这个图片是猫的概率大概是2%，是狗的概率是98%。最后输出这个图片的label：狗。

 

由于假设检验本身的局限性，图片里有别的动物，也不会被识别出来。

 

这么看起来，和假设检验也并没有很大区别吧？classification的第3步，差不多对应假设检验的3-5；classification的第4步对应假设检验的6-7。CatOrDogNet这个预先训练好的网络其实就包含了假设检验里面的test statistics的计算函数——理论上，你也可以从CatOrDogNet得到猫图的分布，和狗图的分布。

 

自然科学和医学领域，现在用的这些经典检验方法（F-test, t-test等），既有个人实验的原因，也有历史进程的原因。一方面，这些实验的各个变量都是被高度控制的，因此一般进行测量、进行比较的也就只有一两个variable，这种情景下正态分布的假设还是挺好用的。

另一方面，绝大多数生物和医学的实验，样本量很低，（3-10属于常态，12-96算是个大样本了，>96的必有高通量这种词），即使不符合正态分布也看不出来（逃）。

（2018-5-20：其实就是不会别的test，你们抓着前面这句话锤的真是逼我说真相）

而机器学习面对的样本对象就要复杂的多，大多数情况下，不要说正态分布，一个良定义的分布都不一定刻画得出来。要不然PCA降维来一套，然后列列式子就好了，搞这么复杂还吃GPU干嘛。对应的statistics很难显性地表述，所以我们才不得不用机器学习的方法。

 

归根结底，假设检验只是统计推断的一种系统化方法而已，而所有机器学习里面做prediction的本质上都是为了做统计推断：你拿到一堆样本数据，从而样本数据估计总体数据的统计特征。

只要你在test set上对模型做测试，那就是在做假设检验。

（2018-5-20：更精确地讲应该是做预测推断（predictive inference），根据观测样本，估计统计特征，从而对未来的观测进行预测。但是预测的准不准，和统计推断的好不好，是两个完全不同的评判标准，ML里面经常追求的往往是前者）

 

机器学习不可避免的一定会应用假设检验的流程。毕竟机器学习本身的方法论也是人设计的，我们常用的除了假设检验之外的统计推断方法，可能就只有模型选择方法了（Model selection）。

 

作者：郭昊天
链接：https://www.zhihu.com/question/55420602/answer/394490229
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 

对大量复杂结构数据想直接使用模型选择？奥卡姆剃刀了解一下，分分钟教你做大人。顶多是在Hyperparameter optimization里面应用一下。

所以不仅机器学习，deep learning，即使明天搞出一个新的办法，利用大数据做统计推断，也一定逃不脱假设检验的框架，除非有什么方法论的剧烈革新。

 

除此之外，机器学习里面经常做的变量重要度估计（estimates of variable importance），很多也类似于假设检验的流程：

1. data里面不一定所有的数据都是真实可靠并且重要的，你不知道怎么理解判断。
2. 你根据已有的data习得一组网络参数。现在我们把一组选定的variable随机打乱，然后重新训练。这时候你的“零假设”就是两次训练的结果应该有类似的参数、预测值、错误等，而“对立假设”就是两次训练的结果有着不同的参数、预测值、错误等，也就是说这个variable对于训练合理的模型是有用的。
3. 然后选一个合适的描述两者之间差异的方式——最简单的就是直接求差。人为设置一些阈值，把没什么用的、帮倒忙的变量选出来。

不过判断的方式一般不是给出一个probability，不过打乱一个变量之后重练的模型在多大概率上等效于真实data训练得到的模型，应该也是可计算的。

 

 

@Jqx1991

提的关于模型不确定性的估计以及困难都是很好的内容，不过没看懂和假设检验有什么关系……

 

 

第二个问题可能比较简单，LR这里指的应该是logistic regression吧，首先这个模型解释性强，其次我觉得使用这个方法其实非常契合医学数据，这和实验数据本身的特征有关系。

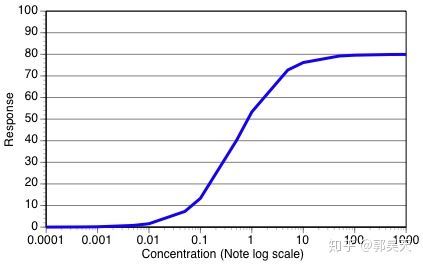
在现阶段，大多数生化、细胞生物学、药学、医学研究的对象，他们的“底层算法”，都能追溯到酶催化生化反应的Briggs-Haldane kinetics。学生物都知道Michaelis-Menten kinetics，就是B-H kinetics的一个特殊形式。Anyway，他们的曲线都是长成这个样子的——数学上变换到对数坐标的话就是个logistic function：

实验中的观测对象，大多是从此衍生出来的，很多还完全符合logistic function。一些复杂体系会由于多次非线性变换而不能用logisitic拟合，但是保留S形曲线的常有，涌现出新特征的则不那么常有。所以用LR还是没问题的。

有钱有技术搞清楚复杂体系的那些课题组一般也都知道应该怎么做更合适的分析。

 

 

 

 

 

宋懿朋

biostatistician

1. 机器学习和医学数据分析关注点不一样。机器学习以prediction为主要的目标，为了提高prediction performance 发展了各种方法。医学数据分析对模型的可解释性要求很高，而且几乎都是小规模的数据，只有几个变量，大量的样本，经典统计非常有效。当然机器学习或者统计学习里面也有针对high dimensional data 的假设检验，在生物信息应用很多。
2. LR的可解释性强，而且模型很简单啊（非常重要，医学院里面的统计学教育非常基础，即使是公共卫生学院）。还有，医学论文里面，每个变量都很重要，都是informative的。在机器学习里面，一个图像里面的pixel本身并没有什么意义。

 

 

 

 

 

 

作者：知乎用户
链接：https://www.zhihu.com/question/55420602/answer/394028426
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 

感觉这个问题下的回答有点两极化了，一说是认为机器学习领域做不来假设检验，一说是认为机器学习研究过程本身就在做假设检验… 我个人认为，传统数理统计中的假设检验之所以没法或者很少被直接迁移到机器学习领域中，有一个很重要的原因就是现在的机器学习模型，比如各种 NN，的参数空间（space of parameters/weights）太大了。要做假设检验，首先要提出假设吧，然后再根据样本点的存在规律去接受或者拒绝该假设。但是在机器学习模型中，比如 CNN，不管模型的 macroarchitecture 还是 microarchitecture 做出改变，整个参数空间其实就已经变了，所谓的优化过程，不过是在假设该参数空间包含了客观真实的 function 的前提下去寻找最优解的过程。谁敢说自己的网络构架就是最接近理想的模型构架呢？如果对一个问题，或者对一堆  样本点，连一个公认可信的假设都提不出来，又要怎么做假设检验呢？

我认为研究假设检验的目的，在于对被测模型的可信度/不确定度进行一个定量描述，与此沾点边的，还有 confidence interval/prediction interval/uncertainty analysis，所以我打算从神经网络的不确定性分析角度抛砖引玉一下。