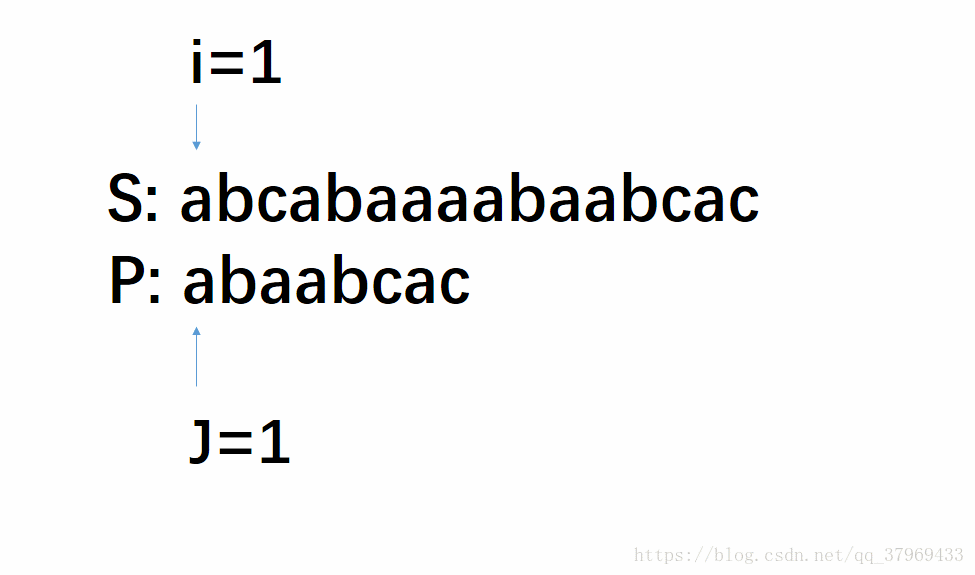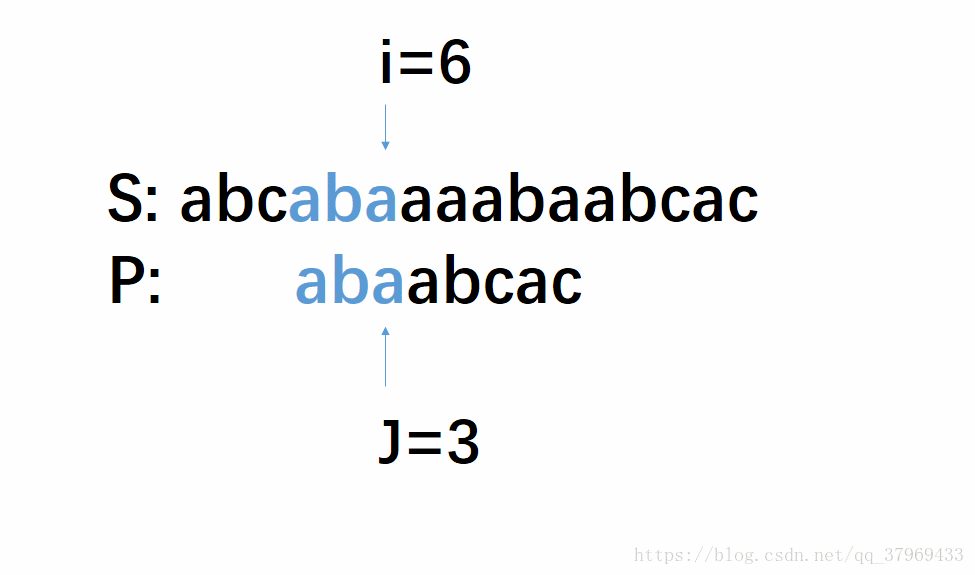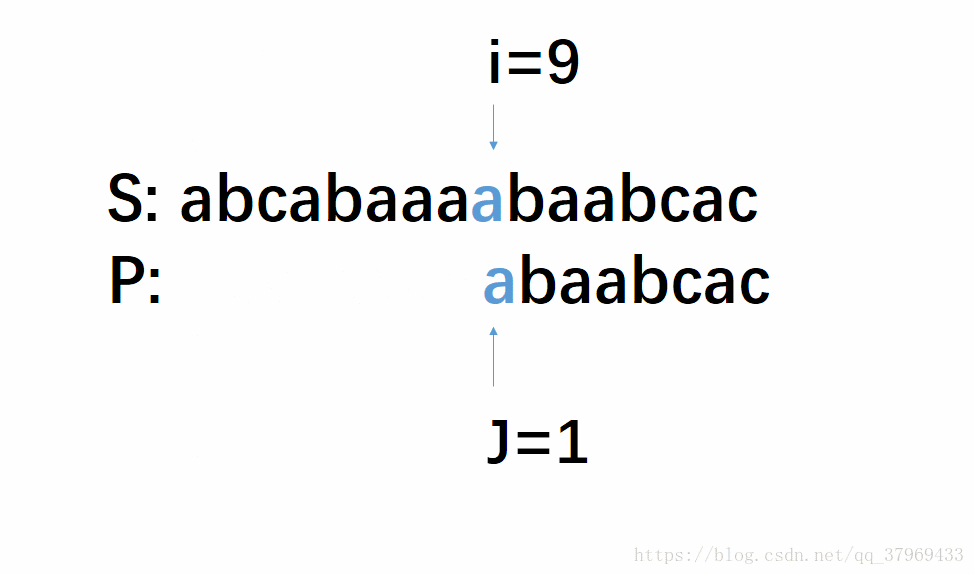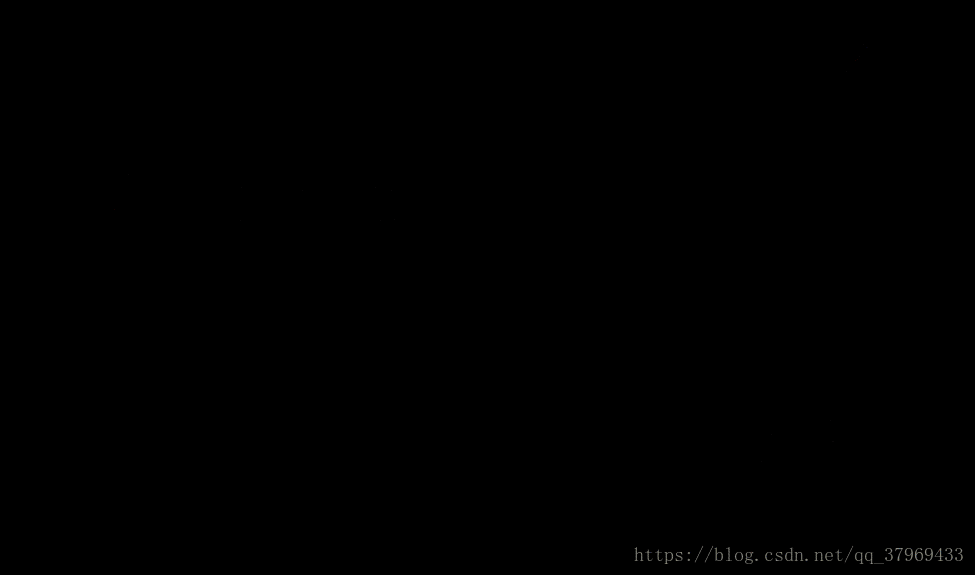算法第一步,拿KMP来开路(2020年最全最简单KMP算法讲解)

目录
1.KMP算法的来源
2.最大公共前后缀
3.KMP算法原理
4.next数组
5.next数组值的确定
6.KMP算法的缺陷
7.KMP算法的改进
8.一道KMP算法题

1.KMP算法的来源

其实博主刚看KMP算法的时候的反应是这样的：

我们引用一个问题

给定一个主串S及一个模式串P,判断模式串是否为主串的子串；若是,返回匹配的第一个元素的位置（序号从1开始）,否则返回0；如S=“abcd”,P=“bcd”,则返回2；S=“abcd”，P=“acb”,返回0

这道题我们最先想到的算法设计思路肯定和下面动图差不多

我们想到这个思路后,直接两层for循环轻松解决,虽然这种朴素算法思路简单而且容易想到,但两个串都有依次遍历,时间复杂度为O(n*m),效率不高,那么为了让效率变高,我们的KMP算法横空出世

2.最大公共前后缀

在正式介绍KMP算法之前我们了解一个概念,一会KMP算法要用到,那就是最大公共前后缀,首先我们介绍前缀后缀

前缀：就是包含第一个字符但不包含最后一个字符的连续子串
后缀：就是包含最后一个字符但不包含第一个字符的连续子串

我们举个例子,列出串abcab的所有前缀后缀
前缀有：

1. a
2. ab
3. abc
4. abca

后缀有：

1. b
2. ab
3. cba
4. bcab

公共前后缀：一个字符串前缀和后缀相同的的字符串
最大公共前后缀：一个字符串前缀和后缀相同的最大长度所代表的字符串

对于abcab来说,公共前后缀只有ab，那么最大公共前后缀为ab

3.KMP算法的原理

朴素算法中，P的第j位失配，默认的把P串后移一位。但在前一轮的比较中，我们已经知道了P的前(j-1)位与S中间对应的某(j-1)个元素已经匹配成功了。就意味着，在一轮的尝试匹配中，我们get到了主串的部分内容，我们能否利用这些内容，让P多移几位(我认为这就是KMP算法最根本的东西)，减少遍历的趟数呢？答案是肯定的。再看下面改进后的动图就是我们KMP算法的匹配过程：

首先我们根据上面的KMP匹配模式图的规律与朴素的算法做一个对比：

朴素算法： 每次失配，S串的索引i定位的本次尝试匹配的第一个字符的后一个。P串的索引j定位到1，T(n)=O(n*m)
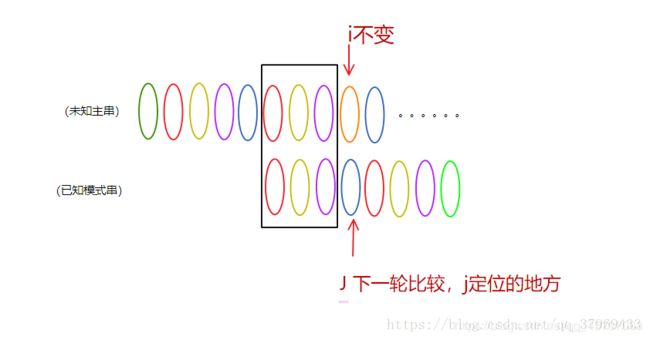
KMP算法： 每次失配，S串的索引i不动，P串的索引j定位到某个数。T(n)=O(n+m)，时间效率明显提高

再看一组KMP算法一次移动图解(相同颜色代表相同的字符)，初始位置如下：

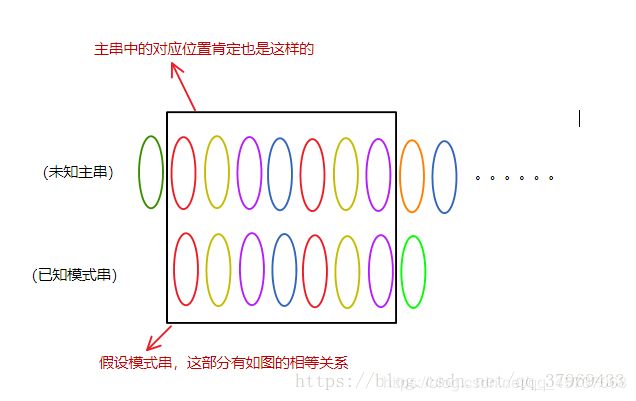
下一步：

你会发现它与朴素的算法有两个区别：

1. 朴素的算法主串指针i会跳到第三个位置，而KMP算法跳到第九个位置
2. 朴素的算法模式串指针j会从第一个字符重新匹配，而KMP算法直接让j在第四个字符和主串的i指针指向的字符进行比较

再重新看看这一句话

KMP算法： 每次失配，S串的索引i不动，P串的索引j定位到某个数。T(n)=O(n+m)，时间效率明显提高

那么我们究竟能在前一轮失败的匹配结果里边得到什么内容，能让S串的索引i不动，P串的索引j定位到某个数呢？

这时候就要借助我们的最大公共前后缀了：在上面的两张图中，第一张图的匹配失败是在模式串的第八个位置，也就是前七个位置都匹配成功，我们根本就不需要再用朴素的匹配方式把主串的匹配指针往后移动一位把模式串的匹配指针重新指向第一个字符。因为模式串再往右移动，只有我们主串的这七个字符的后缀和模式串这七个字符的前缀(也就是这七个字符的公共前后缀)才能完全重合，其他的都不能完全重合，这就是我们找寻公共前后缀的意义，公共前后缀必须是最大的，否则我们往往会错过最佳结果，可以自己找一个例子试一试，博主就不再深究了,这样就可以保证指向我们主串的指针不发生回溯，即主串的i指针之后往后移动，不会往前移动

4.next数组

为了表示下一轮比较模式串j定位的地方，我们将其定义为next[j]，next[j]就是第j个元素前j-1个元素最大公共前后缀所代表字符串的长度个数加1(加1的目的是直接匹配最大公共前后缀的下一位)

针对上面的两张动图,我们可以看出前j-1最大公共前后缀为3,加1就是4,那么下一轮匹配就从第4个字符开始,所有对于上面的那个动图,模式串第8位的next数组值为4即next[8]=4;

也就是说只要我们确定一个模式串所有字符的next数组值，那么就知道了下一次我们模式串匹配所要匹配的初始位置即当发生失配时，i不变，j=next[j]就好啦！接下来就是怎么确定next值了。

那么我们手写一个next数组值,如下面动图(首尾重合个数就是我们的最大公共前后缀)：

我们规定next[1]=0

也就是说:

5.next数组值的确定

虽然我们可以看出来某一个字符串的最大前后缀，但是程序是不能看出来的，要按照某些规律进行推理，那么按照何种规律呢？

首先我们可以从前面的图中推理出next[j+1]的最大值为next[j]+1

为啥呢，我们举个例子:

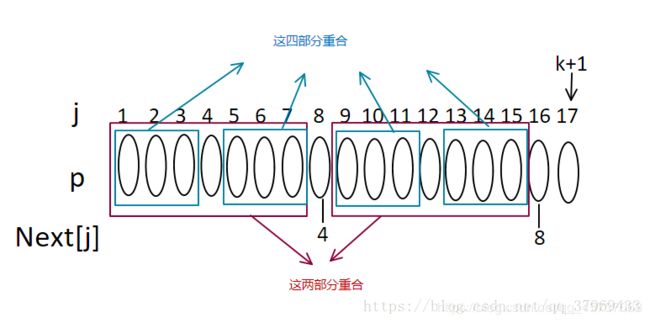
1.下图中我们已知next[16]=8，我们来推理next[17]的值;

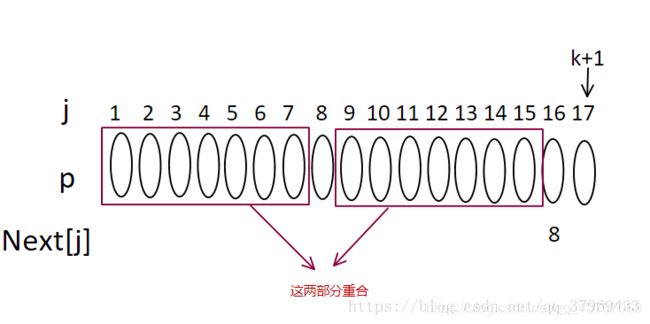
2.如果P8=P16，则明显next[17]=8+1=9(也就是我们所说的next[j+1]的最大值为next[j]+1),可能会有疑问了,如果 P8!=P16该咋推导呢,不急我们一步一步来，如果next[8]=4,即：

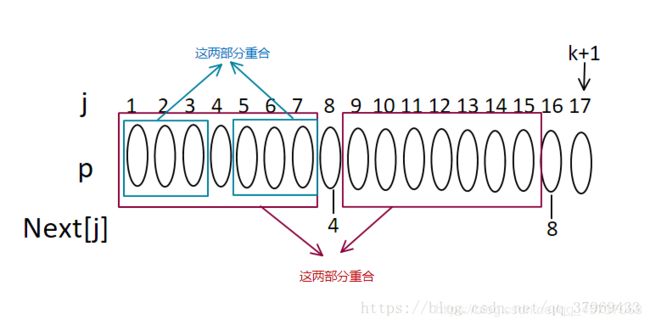
3.再加上已知next[16]=8，那么我们就可以得出如图：

4.那么我们证明这四部分相等得到意义其实就是为了证明如图

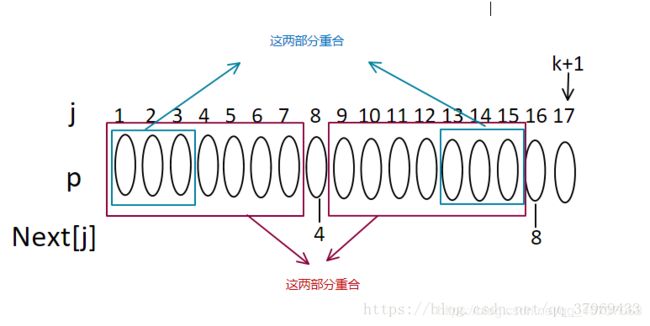
5.现在在判断，如果P16=P4则next[17]=4+1=5，否则，在继续递推，若next[4]=2,那么有下图关系：

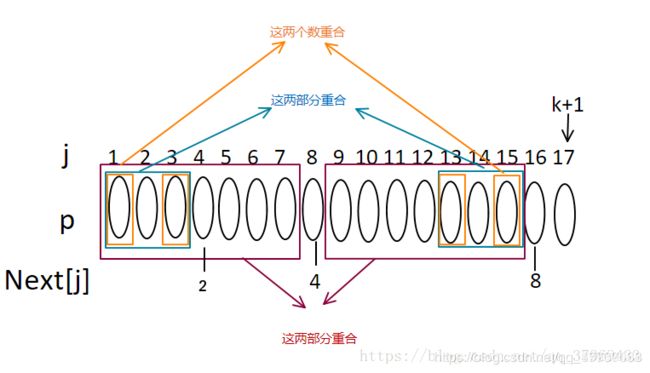
6.若P16=P2，则next[17]=2+1=3;否则继续取next[2]=1、next[1]=0；遇到0时还没出结果，则递推结束，此时next[17]=1

也就是说我们求j的next[j]的值，其实就是前j-1个字符的next的数组值一步一步按照上述方法地推得到

7.求一个字符串的next数组值得代码实现(仔细品完上图再看)

void get_next(char T[],int next[])
{
	int i=1;
	int j=0;
	next[1]=0;
	while(i<T[0])//T[0]为字符串长度
	{
		if(j==0||T[i]==T[j])//T[i]表示后缀的单个字符，T[j]表示前缀的单个字符  
		{
			i++;
			j++;
			next[i]=j; 
		}
		else
		j=next[j];//若字符不相同那么j值回溯 
	} 
}

6.KMP算法的缺陷

KMP算法的改进（卧槽还这么nb的算法还有缺陷？我tm:"…"(虎狼之词)）

比如我们的主串是S="aaaabcde",模式串是P="aaaaax"那么模式串的next数组值我们可以很快写出(自己写一遍)是012345，我们的KMP算法是这么匹配的：

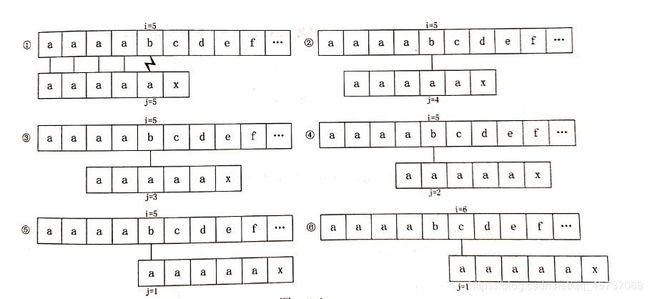
我们观众老爷人均月收入十万肯定随便都看得出来,博主看了好一会

我们可以看出第一步失配的时候是在第五个位置，失配的字符为a，那么此时第二步KMP算法是跳到第五个字符的next数组值(next[5]=4)里进行匹配,但是模式串第四个字符还是a，上一个a都已经匹配失败了，这一个a肯定也是失败，换句话来说，这个匹配就是多余的，我们看之后KMP的好几步都是a与主串第一次失配的b进行匹配，所以这几步都是多余的，这就是KMP算法的缺陷

7.KMP算法的改进

其实挺简单，就是加一步当前模式串失配的字符和next数组对应位置的字符进行比较一次，如果相同那么直接再进行一次j=next[j]不相同就再次进行模式串和主串的匹配

我们把改进后的数组名称为nextval,我们简单推导一下nextval的数组各个值得确定过程

比如模式串为T="abab"

失配位置	next数组值	分析	netival数组值
第一个字符a	next[1]=0	默认的第一个字符的nextval的字符为0	nextval[1]=0
第二个字符b	next[2]=1	模式串失配时的字符为b,next表示的下一个匹配字符为a,不相同所以和next[2]值相同	nextval[2]=1
第三个字符a	next[3]=1	模式串失配时的字符为a,next表示的下一个匹配字符也是a,相同所以不需要再次比较，所以就需要地推一下发现当nextval[3]=nextval[1]=0的时候，才需要进行下次匹配，等于0就是主串的匹配指针右移动一位	nextva[3]=0
第四个字符b	next[4]=2	由于模式串失配位置为b，next数组指向的下一个匹配字符也是b，所以需要我们进一步递推，当netival[4]=netival[2]=1的时候，此时下一轮匹配的字符是a不是b所以可以进行下一轮的匹配	nextval[4]=1

其实和next数组差不多，nextval数组索引大的值可以被nextval数组索引小的值推导出来

代码实现：

void get_nextval(char T[],int nextval[])
{
	int i=1;
	int j=0;
	nextval[1]=0;
	while(i<T[0])//T[0]为字符串长度
	{
		if(j==0||T[i]==T[j])//T[i]表示后缀的单个字符，T[j]表示前缀的单个字符  
		{
			i++;
			j++;
			if(T[i]!=T[j])
			nextval[i]=j;
			else
			nextval[i]=nextval[j]; 
		}
		else
		j=nextval[j];//若字符不相同那么j值回溯 
		
	} 
}

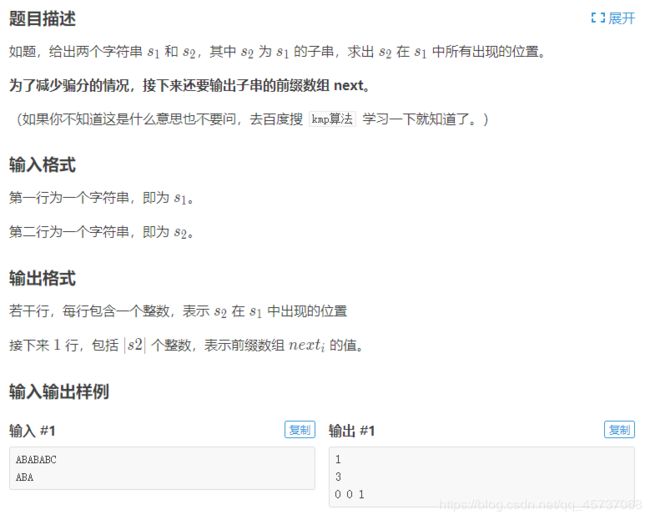
8.一道KMP算法题

AC代码：

#include
#include
#define MAXN 1000010
using namespace std;
int kmp[MAXN];
int la,lb,j; 
char a[MAXN],b[MAXN];
int main()
{
    cin>>a+1;
    cin>>b+1;
    la=strlen(a+1);
    lb=strlen(b+1);
    for (int i=2;i<=lb;i++)
	   {     
	   while(j&&b[i]!=b[j+1])
        j=kmp[j];    
       if(b[j+1]==b[i])j++;    
        kmp[i]=j;
       }
    j=0;
    for(int i=1;i<=la;i++)
	   {
          while(j>0&&b[j+1]!=a[i])
           j=kmp[j];
          if (b[j+1]==a[i]) 
           j++;
          if (j==lb) {cout<<i-lb+1<<endl;j=kmp[j];}
       }

    for (int i=1;i<=lb;i++)
    cout<<kmp[i]<<" ";
    return 0;
}

参考博客：https://blog.csdn.net/qq_37969433/article/details/82947411