2017年7月28日
一、背景
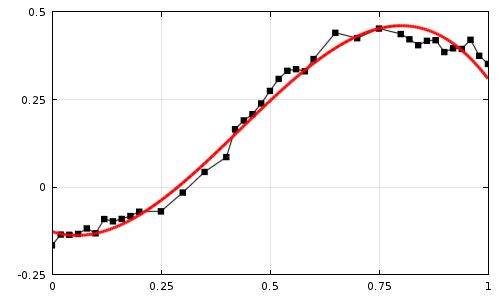
绘制趋势图时,曲线有“锯齿感”,不够顺滑、优美。亟待优化之。
二、回顾绘制过程
1. 根据数据,转化成画布上的 X,Y 坐标;
2. 描点;
3. 连线。
而当数据点足够多的时候,即点与点之间非常密集,在视觉上便成了一条连续的线。(如首图所示的趋势图,则是由 1440 个点组成)
得出不顺滑的原因
它本质上是一条比较密集的折线图罢了,其中的“折线”便是导致不顺滑的原因。
而我们的解决方案很简单: 两点之间不用直线相连,而是用一条曲线把所有数据点连接起来。
三、平滑曲线
我们的问题可以归纳为:已知一组离散值,寻求最符合这些数据的函数方程。
思路 1:“拟合”
拟合法:已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1, λ2,…,λn),使得该函数与已知点集的差别(最小二乘意义)最小。
首先根据离散点的形态,我们预先选择一种函数类型,比如多项式函数、幂函数、指数函数、对数函数、三角函数等。然后求出函数方程中的所有未知数(如使用"最小二乘法"),便得到了这条曲线方程。
( 注:上图来自网络 )
但这样得到的曲线方程并不一定完美的经过所有给出的数据点,它只是尽可能的描述数据变化的趋势。
这不符合我们的业务场景,我们的 GMV 增长趋势图,不仅要求展示变化趋势,还要精确展示每个返回的数据点的位置。
思路 2:“插值”
插值法:利用函数f (x)在某区间中已知的若干点的函数值,作出适当的特定函数,在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
多项式插值 是最直观的一种插值方法,但这种方式会出现数值不稳定问题(龙格现象)。另外,canvas 的 api 在提供绘制线条方面,只有直线、圆弧、二次贝塞尔曲线、三次贝塞尔曲线,无法直接绘制多项式函数方程。
既然直接的多项式插值方式不行,我们再来看看 样条函数插值。
什么是样条函数?
早期工程师制图时,把富有弹性的细长木条(所谓样条)用压铁固定在样点上,在其他地方让他自由弯曲,由这样的样条形成的曲线在连接点处具有连续的坡度与曲率,然后画下长条的曲线,称为样条曲线。
样条插值,即是将已知节点固定,其他地方自由弯曲,即为样条插值函数曲线,从而求得插值点的函数值。
( 注:上图来自网络 )
那么,我们只需在两个点之间,找到一条符合spline function特性(在各段交接处有一定光滑性的函数)贝塞尔曲线描述的曲线,把点连起来就完成了。
如何保证“连接处的光滑性”?
两个分段函数连接处的斜率相等,就顺滑了。
于是就有了 Hermite插值(也称带导数的插值问题),这种插值方式保证了相同的斜率。
那么具体如何实现呢?
四、D3.js 中的 monotone 算法实现
D3.js 中提供了多种构造曲线的算法,如:
d3.curveBasis 基于B样条
d3.curveCatmullRom 基于Catmull–Rom样条
d3.curveMonotoneX和d3.curveMonotoneY,基于 Hermite 型的插值
其中 monotone 算法保证了曲线的单调性,非常适合于这种 GMV 增长趋势图的场景,但这种方式相对而言,会降低一定的平滑度。
我们先来回顾一下我们打算做什么?我们打算在每两个数据点之间,用一条条三次贝塞尔曲线连接起来。曲线与曲线之间要平滑过渡,让人感觉就是一条完整的曲线把所有点都连了起来。
三次贝塞尔曲线
context.bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y);
使用三次贝塞尔曲线,需要知道两个控制点的坐标。
(注:上图是以 monotoneX 为例子的,monotoneY 和 monotoneX 基本一样,就是x,y换个位置)
由于保持 X 轴方向单调性 ,贝塞尔的两个控制点在 X 方向上,均匀放置即可(1/3和2/3处),故控制点 P1 的 x 值为 x0 + dx;P2 的 x 值为 x1 - dx;
假设我们已知线段 A-P1 的斜率 t0, 线段 P2-b 的斜率 t1,则可控制点 P1 的 y 值可表示为 y0 + dx * t0;P2 的 y 值可表示为 y1 - dx * t1;
如何求斜率 t0 和 t1 ?
推导过程在 Steffen, M. 1990. A Simple Method for Monotonic Interpolation in One Dimension. 1990. 论文中有详细阐述。
此论文的推导过程,我没有完全看懂,只能记录一下我认为比较重要的几点:
(1) 构造三次多项式函数(因为它是三次贝塞尔函数的基础形态) [站外图片上传中...(image-20bb55-1519960677536)]
(2)一条曲线的形状,不仅由该段曲线的始节点和终节点决定,也受到紧跟着的第三个节点的影响。故求解每个 t0 和 t1, 需要三个数据点。
(3)上一段曲线与下一段曲线,在连接处的斜率相等(对应的导数值相等),即满足Hermite 型的插值。这将作为一个关键等式,加入到求解之中。
最后推导出来的公式为:
a. 斜率 t1
论文中还使用了 fortran 语法把上述公式精简成:
Y1(i) = (SIGN(1.0, S(i-1) + SIGN(1.0, S(i))) * MIN(ABS(S(i-1)), ABS(S(i)), 0.5*ABS(P(i)))
b. 斜率 t0
D3.JS 中代码实现便是依照以上公式写得,如下:
// 斜率 t1
function slope3(that, x2, y2) {
var h0 = that._x1 - that._x0,
h1 = x2 - that._x1,
s0 = (that._y1 - that._y0) / (h0 || h1 < 0 && -0),
s1 = (y2 - that._y1) / (h1 || h0 < 0 && -0),
p = (s0 * h1 + s1 * h0) / (h0 + h1);
return (sign(s0) + sign(s1)) * Math.min(Math.abs(s0), Math.abs(s1), 0.5 * Math.abs(p)) || 0;
}
// 斜率 t0
function slope2(that, t) {
var h = that._x1 - that._x0;
return h ? (3 * (that._y1 - that._y0) / h - t) / 2 : t;
}
五、最终效果
六、相关链接
- Smoother Signatures-Capturing even more beautiful signatures on Android.-by Rob Dickerson.
- Paper:Cubic spline curve
- Github:osuushi/Smooth.js
- D3.js Curves
- Smooth Bézier Spline Through Prescribed Points
- 根据多个点使用canvas贝赛尔曲线画一条平滑的曲线