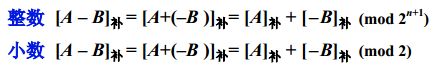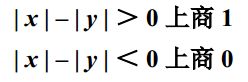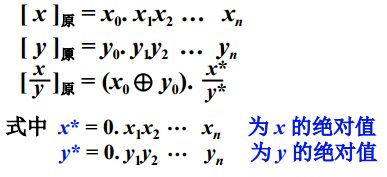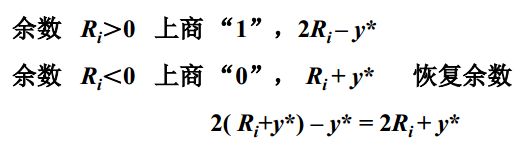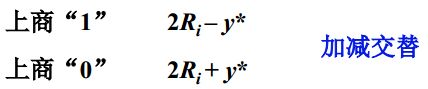计算机组成原理12----定点运算

在计算机中，定点数是如何完成基本移位，加减乘除运算的。

定点运算

1.移位运算

对于二进制数据，左移绝对值变大，右移绝对值变小

对于原码，反码以及补码的移位操作各有不同

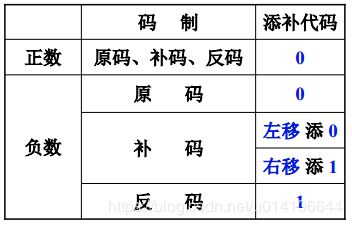
算术移位规则  符号位不变

                                                            

对于正数，原码反码补码左移或者右移添补代码0

对于负数，原码  左移右移填补代码0； 对于补码，左移添0 右移添1；对于反码，左移右移都添1

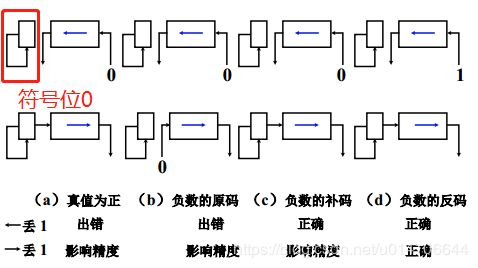
算数移位的硬件实现

                                                 

对于正数，符号位为0，因此左移添0，如果最高位1左移舍去，则结果出错；右移通过符号位右移实现，如果低位1右移舍去则影响精度。

对于负数原码，负数补码和负数反码原理一致。

算数移位：有符号数的移位  逻辑移位：无符号数的移位

逻辑移位：左移时高位舍去 低位添0   右移时低位舍去 高位添0

01010011逻辑左移10100110  算数左移00100110

算数左移时可能会将高位舍掉，可以采用带进位的移位操作

左移时，符号位进入Cy，最高位可以避免移除

2.加法减法运算

使用补码来表示数值，减法运算可以通过加法运算来实现

对于A+B

对于A-B

计算[-B]补时，可以通过[B]补连同符号位取反，末尾加一来实现

将符号位和数值位进行加运算，将符号位产生的进位丢掉

由于定点数表示数值范围有限，加减运算结果可能可能会产生溢出

溢出判断

一位符号位进行判断

对于加法   正数+正数  负数+负数   对于减法   正数-负数  负数-正数  可能会产生溢出

对于操作两个数，如果符号相同，而结果与原操作数符号不同，则为溢出

将最高有效位进位和符号位进行异或，如果结果为1，则说明产生溢出

例如 A=-11/16  B=-7/16  求[A+B]补

A=-0.1011=1.1011   B=-0.0111=1.0111

[A]补=1.0101  [B]补=1.1001

[A+B]补=[A]补+[B]补=10.1110  最高位1丢掉得0.1110 符号位0与操作数符号位不一致，则发生溢出

两位符号位判断溢出

两位符号位小数补码定义：

当两个符号位不同时，表示溢出；最高符号位代码真正符号

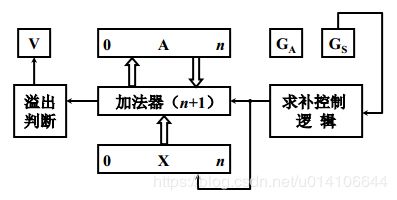
补码加减法硬件配置

                                                              

A中存放加法  X中存放被加数  GA加法标记  GS减法标记

如果为减法，由求补控制逻辑，求出X的补，然后利用加法器将A和X相加；由溢出判断电路判断是否溢出，标记放入V中

3.乘法运算

笔算乘法步骤如下：

A=-0.1101  B=0.1011   运算结果符号位负，将两者绝对值进行相乘，得到最终结果-0.10001111

笔算乘法改进：对于A乘以0.1011化简可以得到下式

                                                    

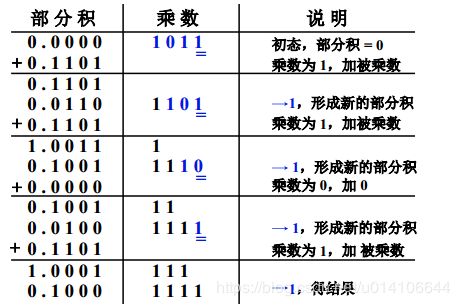
设置部分积初始=0，观察乘数的最低位，乘以乘数A与部分积相加，右移一位得到新的部分积；

观察乘数的左边第二位，乘以乘数A与新部分积相加，右移一位得到新的部分积；

如此，直到乘数的所有位都考虑过，即乘数的每一位0或者1决定了被乘数与部分积的加法操作，乘数的不同位具有不同的权重，因此需要进行移位操作。

笔算乘法过程改进如下：

                                                   

部分积初始化=0，每一次观察乘数的低位0或者1，将部分积+被乘数x乘数低位，然后右移一位，作为新的部分积；

每完成一次操作，则将乘数右移一位，高位用来存放部分积的右移低位

可知乘法可以通过加法和移位运算来实现

原码一位乘

以小数为例：

                                                          

可以最终结果，符号位由两个操作数符号位异或产生；数值部分由两部分绝对值相乘产生

原码一位乘递推公式：

                                                         

Zi为第i次部分积，初始化为零，依次考察y从最低位到最高位每一位，与x*相乘加部分积，进行移位操作，得到新的部分积，直到y已经到达最高位停止。此时最终结果存放于部分积中

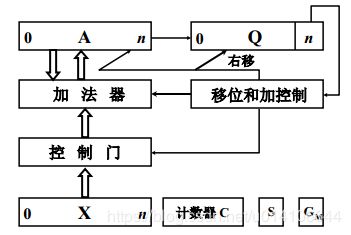
原码一位乘硬件配置

                                                             

 

GM为乘法标记，S存放乘积符号，计数器C控制逐位相乘次数

X存放被乘数原码   Q存放乘数原码   A中存放部分积初始化为零

乘数Q  Qn=1 则A+X，然后A,X右移一位；Qn=0 则A,X右移一位 其中A中部分积右移的低位放于Q中高位中

最终运算结果存放于AQ中

4.除法运算

笔算除法分析

A=-0.1011  B=0.1101  商符号单独处理   绝对值相除

对于笔算除法，比较除法和被除数绝对值大小来确定商；然后余数不动，低位补0，减去右移一位的除数；

对于机器除法来说，符号位可以由异或操作完成

对于余数绝对值为|x|,除数绝对值为|y|,则商可以由余数和除数绝对值大小来确定0或者1

当确定商之后，可以将余数左移低位补0，减去除数，来得到新的余数

原码除法

以小数为例：

符号位由异或产生，数值部分为两者绝对值相除

对于机器除法来说，初始余数=被除数，每一次需要判断余数绝对值和除数绝对值大小，由于减法操作需要使用加法来完成

恢复余数法

商值由被除数和除数绝对值大小来确定，计算机中只设加法器，因此x-y需要转化为   x补+（-y）补

如果x-y得到余数小于零，则说明商=0，此时需要恢复余数，即将余数加上y

例：x=-0.1011  y=-0.1101  求(x/y)补

x原=1.1011  y原=0.1101  y*补=0.1101  （-y*）补=1.0011

具体计算过程如下：

对于每一次操作，比较余数和除数绝对值大小来决定商的值，

如果余数为负，则需要恢复原来余数的值，商为0，将余数逻辑左移，

如果余数为正，则商为1，将余数逻辑左移。

加减交替法

当余数R>0时，商=1，将余数左移减去除数，即 2R-y

当余数R<0时，商=0，将余数+除数   左移一位，减去除数，即 2(R+y)-y=2R+y

因此，可以根据余数的符号来判断下一次余数的数值

上述例子计算过程如下：

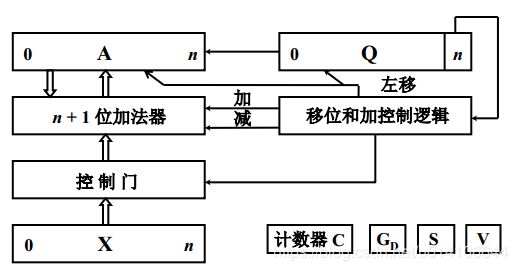
原码除法加减交替法硬件配置

                                        

GD为除法标记  V为溢出标记  S为尚符  计数器C控制逐位相除次数n

A存放被除数原码    X存放除数原码

Q中存放余数，

当Qn=1时，说明余数小于零，商=0 被除数左移一位减去除数

当Qn=0时，说明余数大于零，商=1 被除数左移一位加上除数