SVM算法编程练习

1.增加了一个超参数 C C 来控制正则项的重要程度。 C C 越小容错空间越大。

代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X [y<2,:2] #只取y<2的类别，也就是0 1 并且只取前两个特征
y = y[y<2] # 只取y<2的类别
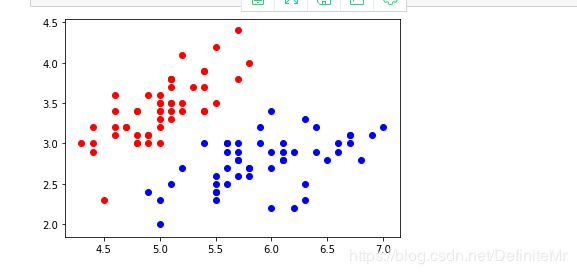
# 分别画出类别0和1的点
plt.scatter(X[y==0,0],X[y==0,1],color='red') 
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()
# 标准化
standardScaler = StandardScaler()
standardScaler.fit(X) #计算训练数据的均值和方差
X_standard = standardScaler.transform(X) #再用scaler中的均值和方差来转换X，使X标准化
svc = LinearSVC(C=1e9) #线性SVM分类器
svc.fit(X_standard,y) # 训练svm

运行结果：

1.1绘制这个决策边界

代码：

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
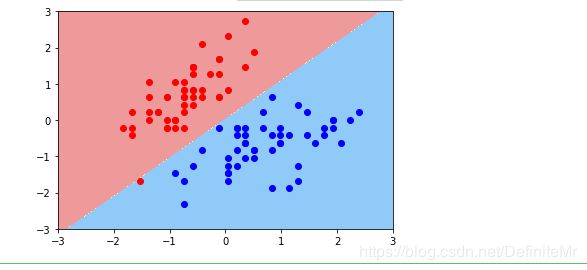
# 绘制决策边界
plot_decision_boundary(svc,axis=[-3,3,-3,3]) # x,y轴都在-3到3之间
# 绘制原始数据即散点图
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red') 
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

运行结果：

再次实例化SVC，重新传入一个较小的C：
代码：

svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard,y)
plot_decision_boundary(svc2,axis=[-3,3,-3,3]) # x,y轴都在-3到3之间
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red') 
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

运行结果：

2.使用多项式特征和核函数~

加载月亮数据集，查看X与y的维度：
代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
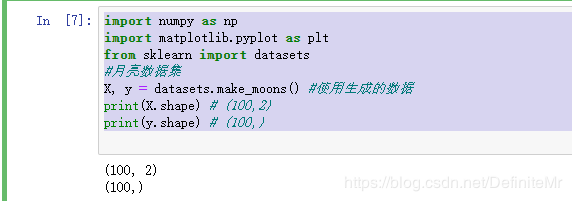
#月亮数据集
X, y = datasets.make_moons() #使用生成的数据
print(X.shape) # (100,2)
print(y.shape) # (100,)

运行结果：

接着绘制散点图：
代码：

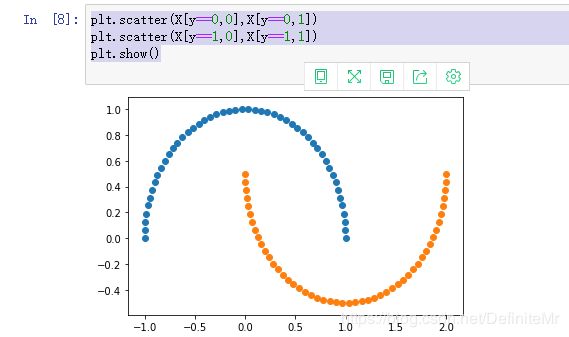
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果：

生成的数据像月亮，这就是它函数名称的由来。但是生成的数据集太规范了，我们增加一些噪声点。
我们接下来通过多项式特征的SVM来对它进行分类。
这里我们引入了管道，它可以将许多算法模型串联起来，比如将特征提取、归一化、分类组织在一起形成一个典型的机器学习问题工作流。
代码：

from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),#生成多项式
        ("std_scaler",StandardScaler()),#标准化
        ("linearSVC",LinearSVC(C=C))#最后生成svm
    ])
poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X,y)
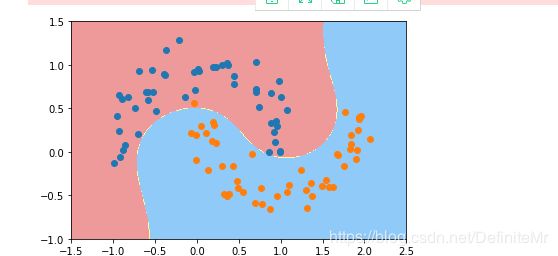
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果：

我们可以看到，生成的边界不再是线性的直线了。

我们还可以使用核技巧来对数据进行处理，使其维度提升，使原本线性不可分的数据，在高维空间变成线性可分的。再用线性SVM来进行处理。

核技巧来对数据进行处理:

from sklearn.svm import SVC
def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("kernelSVC",SVC(kernel="poly")) # poly代表多项式特征
    ])
poly_kernel_svc = PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果：

3.核函数

3.1产生测试点以及绘制散点图

代码：

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-4,5,1)#生成测试数据
y = np.array((x >= -2 ) & (x <= 2),dtype='int')
plt.scatter(x[y==0],[0]*len(x[y==0]))# x取y=0的点, y取0，有多少个x，就有多少个y
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

运行结果：

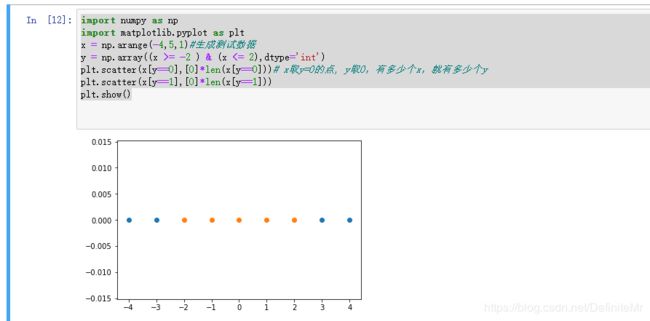
接下来使用高斯核函数，看如何将一个一维的数据映射到二维的空间：

def gaussian(x,l):
    gamma = 1.0
    return np.exp(-gamma * (x -l)**2)
l1,l2 = -1,1
X_new = np.empty((len(x),2)) #len(x) ,2
for i,data in enumerate(x):
    X_new[i,0] = gaussian(data,l1)
    X_new[i,1] = gaussian(data,l2)    
plt.scatter(X_new[y==0,0],X_new[y==0,1])
plt.scatter(X_new[y==1,0],X_new[y==1,1])
plt.show()

运行结果：

4.超参数 \gamma γ

\gamma γ 越大，高斯分布越窄； \gamma γ 越小，高斯分布越宽。

接下来用代码来演示下 \gamma γ 的取值对结果的影响。
首先是生成我们的数据:

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
#月亮数据集
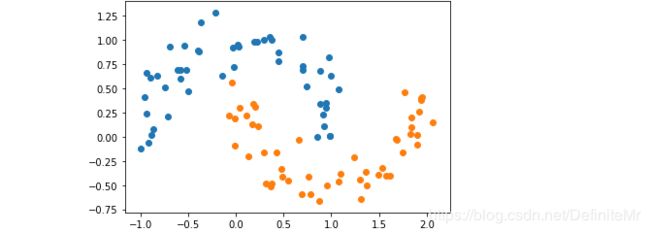
X,y = datasets.make_moons(noise=0.15,random_state=777)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果：

接下来定义一个RBF核的SVM：

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
svc = RBFKernelSVC()
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

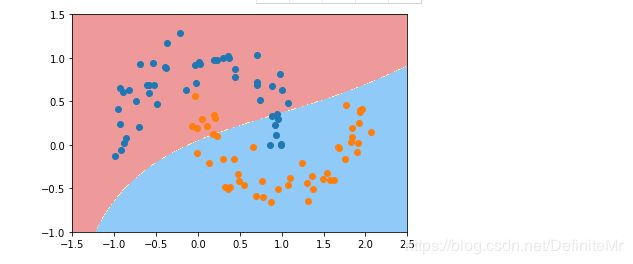
运行结果：

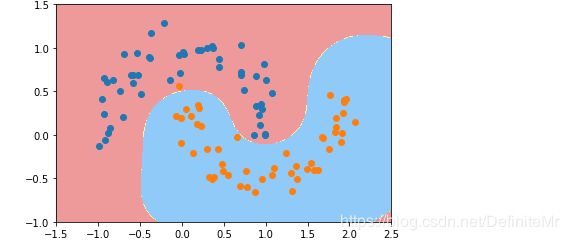
这是我们设置 \gamma=1.0 γ = 1 . 0 时所得到的决策边界。我们调整下它的值再试下：

svc = RBFKernelSVC(100)

其他代码不变：

即：

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])
svc = RBFKernelSVC(100)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

运行结果：

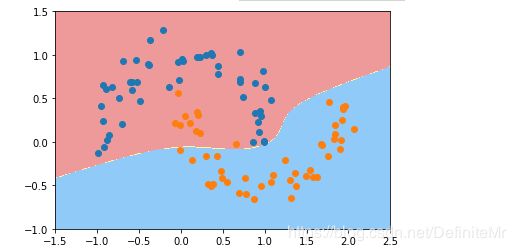
\gamma γ 取值越大，就是高斯分布的钟形图越窄，这里相当于每个样本点都形成了钟形图。很明显这样是过拟合的。
我们再设一下 \gamma γ

svc = RBFKernelSVC(10)
结果：

再调小一点:

svc = RBFKernelSVC(0.1)
运行结果：

此时它是欠拟合的。

最后
做一个回归问题：
代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=777) # 把数据集拆分成训练数据和测试数据
from sklearn.svm import LinearSVR 
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
def StandardLinearSVR(epsilon=0.1):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('linearSVR',LinearSVR(epsilon=epsilon))
    ])
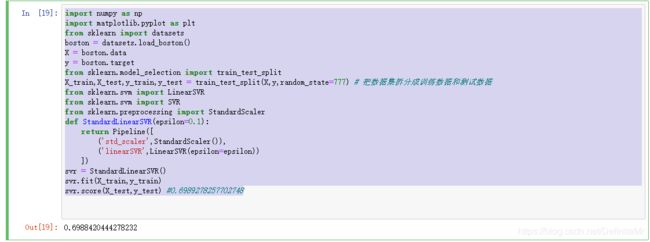
svr = StandardLinearSVR()
svr.fit(X_train,y_train)
svr.score(X_test,y_test) #0.6989278257702748

运行结果：

参考文献：参考网址