八大排序算法总结之一（冒泡排序，快速排序，直接插入排序，希尔排序）

概述：
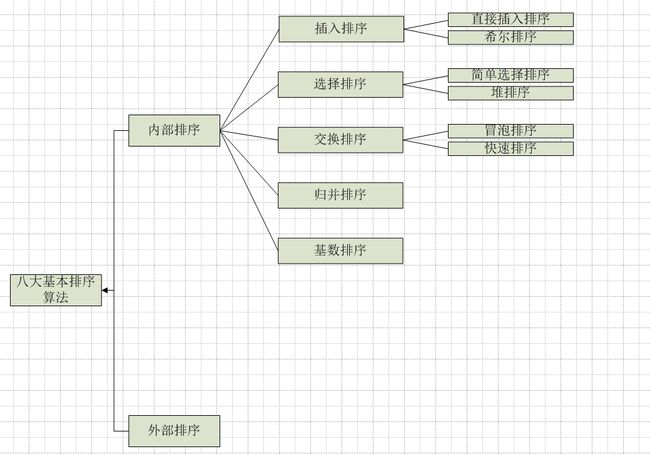
排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序一般是排序的数据量很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。我们经常说的八大排序说的就是内部排序。

---

冒泡排序算法：（从后往前）bubbleSort

• 比较相邻的两个数，若前面的数大于后面的数，则交换两个数；
• 这样对0到n-1个数据进行遍历，那么最大的数据就会被排到n-1处；
• 重复步骤，直至再也不能交换。

public static void bubbleSort1(int [] input,int n){
        //外围循环n-1次，每次确定一个元素的位置，位于尾部
        for(int i=0;i1;i++){
            //内部循环，相邻元素进行比较，比较次数逐步减1
            for(int j=0;j1-i;j++){
                //从小到大排序
                if(input[j]>input[j+1]){
                    int temp = input[j];
                    input[j] = input[j+1];
                    input[j+1] = temp;
                }
            }
        }

    }

对于一些数据，前面部分是乱序的，而后面部分是有序的。当前面的排序好后，后面的元素排序还需要重复前面的操作，这种做法是非常多余的。对与这种情况可以做出优化，比如加上一个标志（flag），初始值为false，有交换则置为true，如果某次排序没有交换元素，则表明后面的元素是有序的，跳出循环，排序结束。

public static void bubbleSort2(int [] input,int n){
        //外围循环n-1次，每次确定一个元素的位置，位于尾部
        for(int i=0;i1;i++){
            //标记位，如果这一趟发生了交换，则为true，否则为false。明显如果有一趟没有发生交换，说明排序已经完成。
            boolean flag = false;
            //内部循环，相邻元素进行比较，比较次数逐步减1
            for(int j=0;j1-i;j++){
                //从小到大排序
                if(input[j]>input[j+1]){
                    int temp = input[j];
                    input[j] = input[j+1];
                    input[j+1] = temp;
                    //发生交换，置flag为true
                    flag=true;
                }
            }
            //没有发生交换，则表明已是有序，跳出循环
            if(flag==false){
                break;
            }
        }       
    }   

时间复杂度O(n^2) , 算法稳定性：稳定（如果两个元素相等，我想你是不会再无聊地把他们俩交换一下）

---

快速排序算法（快排）：quickSort

它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
注意：第一遍快速排序不会直接得到最终结果，只能确定一个数的最终位置。为了得到最后结果，必须继续分解数组，直到数组不能再分解为止（只有一个数据），才能得到正确结果。

• 先从数列中取出一个数作为基准数
• 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
• 再对左右区间重复第二步，直到各区间只有一个数。

快速排序算法是基于分治法的：

分治法+挖坑（ 先从后向前找，再从前向后找）：
3 4 6 8 9 10 5 2 16
首先选定一个枢纽数3，pivotkey=a[0] ， a[0]被保存到pivotkey中，可以被认为，在a[0]上挖了一个坑，可以将其他数据填充到这里来。然后从后向前找到小于pivotkey的值2，a[0]=a[7]，a[0]上的坑被a[7]填上，结果又形成了一个新坑a[7].

public static void quickSort(int low,int high,int []input){
        if(lowint pivotloc = partion1(low,high,input);
            quickSort(low,pivotloc-1,input);
            quickSort(pivotloc+1,high,input);
        }   
    }
    public static int partion1(int low,int high,int[]input){
        //开始挖坑，input[low]为枢纽，其值保存在pivotkey中，可以将其他数据填充过来
        int pivotkey = input[low];
        while(low//从后向前，直到找到小于pivotkey的值
            while(low=pivotkey){
                high--;
            }
            //加上判断条件是因为当high==low，不必操作下面的语句
            if(low//在low的位置上填坑，又形成了一个新坑
                input[low] = input[high];
                //从下一个位置开始
                low++;
            }
            //从前向后，直到找到大于pivotkey的值
            while(lowif(low//在high的位置上填坑，又形成了一个新坑
                input[high]=input[low];
                //从下一个位置开始
                high--;
            }
        }
        //****low==high,退出时，将pivotkey填到这个坑****pivotkey一直只是用与比较没有被填充过，当low==high，将其填充
        input[low] = pivotkey;
        return low;
    }

分治法，但不挖坑，交换的方法。最后的那个坑不需要去填，因为在交换的过程中，已经处理好了。这样，没交换一次就需要进行3次赋值语句，而实际上，在排序过程中对枢纽节点的赋值是多余的。只需最后赋值，也就是上面的做法。下面是没有改进前的方法。

public static void quickSort(int low,int high,int []input){
        if(lowint pivotloc = partion2(low,high,input);
            quickSort(low,pivotloc-1,input);
            quickSort(pivotloc+1,high,input);
        }   
    }
public static void swap(int[] input,int begin,int end){
        int temp = input[begin];
        input[begin] = input[end];
        input[end] = temp;
    }

public static int partion2(int low,int high,int[]input){
        //枢纽节点
        int pivotkey = input[low];
        while(low//从后向前，直到找到小于pivotkey的值
            while(low=pivotkey){
                high--;
            }
            //加上判断条件是因为当high==low，不必操作下面的语句
            if(low//交换
                swap(input,low,high);
                //从下一个位置开始
                low++;
            }
            //从后向前，直到找到大于pivotkey的值
            while(lowif(low//交换
                swap(input,low,high);
                //从下一个位置开始
                high--;
            }
        }
        //返回之前没有填坑，是因为在交换过程中已经完成
        return low;
    }

有时是以中间的数作为基准数的，要实现这个非常方便，直接将中间的数和第一个数进行交换就可以了。时间复杂度O（nlogn）, 算法稳定性：不稳定。

---

直接插入排序： insertSort

直接插入排序(Insertion Sort)的基本思想是：每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

直接插入排序时使用顺序查找，找到关键字应该插入的位置，然后将该位置后面的所有元素向后移动。然后将要插入的值插入目标位置。

public static void insertSort(int []input){
        for(int i=1;i//用来标记临界点
            int j=i-1;
            for(;j>=0;j--){
                //插入input[i]时，前面的都是有序的序列，直到找到一个小于input[i]的值input[j]，那么该位置后面的一个位置就是input[i]的位置
                if(input[j]break;
                }
            }
            //j==i-1,表明input[i]前面的一个数input[i-1]就小于input[i],就不必移动数组了
            if(j!=i-1){
                int temp = input[i];
                for(int k=i-1;k>j;k--){
                    input[k+1] = input[k];
                }
                //标记点的后一位就是input[i]的位置
                input[j+1]=temp;
            }       
        }
    }

改进（折半插入排序）：在直接插入排序时，采用折半查找的方法找到插入的标记点，然后将标记点后面的元素从后向前依次移动一个位置。

public static void bInsertSort(int []input){
        for(int i=1;iint low=0;
            int high = i-1;
            //high作为标记节点，input[high]
            while(high>=low){
                int middle = (low+high)/2;
                if(input[middle]1;
                else
                    high=middle-1;
            }
            //保存input[i]
            int temp = input[i];
            for(int k=i-1;k>high;k--){
                input[k+1] = input[k];
            }
            input[high+1] = temp;           
        }
    }

折半插入排序所需附件的存储空间和直接插入排序相同，从时间复杂度上来讲，折半插入排序仅仅减少了关键字之间的比较次数，但移动次数不变。因此时间复杂度还是O（n^2）. 算法稳定性：稳定。

改进：直接插入排序时，将收索和后移两个动作同时进行。

public static void insertSort3(int []input){
        for(int i=1;i//0~i-1位为有序，若第i位大于i-1位，忽略此次循环，相当于continue
            if(input[i-1]>input[i]){
                int temp = input[i];
                int j = i-1;
                //收索和移动同时进行
                for(;j>=0&&input[j]>temp;j--){
                    //input[j]后移一位，在input[i]处挖了一个坑
                    input[j+1] = input[j];
                }
                input[j+1] = temp;
            }
        }
    }

再对上面的方法进行改写， 用数据交换代替数据后移。

public static void insertSort2(int []input){
        for(int i=1;ifor(int j=i-1;j>=0;j--){
                //基于有i前面的元素数有序的，交换之后input[i]的值向前移动了一位，直到有input[j]
                if(input[j]>input[j+1]){
                    int temp = input[j];
                    input[j] = input[j+1];
                    input[j+1] = temp;
                }
            }
        }
    }

---

希尔排序：：shellSort

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。
基本思想是：先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2(d2小于d1),重复上述的分组和排序;依次取d3、d4、…..直至取到dt=1为止,即所有记录放在同一组中进行直接插入排序。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;

public class ShellSort {
    public static void shellInsert(int[]input,int dk){
        /*
         * 对数组做一趟希尔排序。本算法和直接插入排序相比，做了如下修改：
         * 前后记录位置的增量是dk，而不是1;
         * */
        //所有距离为dk的倍数的记录放在同一个组中，对组内元素进行直接插入排序
        for(int i=dk;iif(input[i-dk]>input[i]){
                //用于保存将要插入有序分组的元素input[i]
                int temp = input[i];
                ////收索和移动同时进行
                int j = i-dk;
                for(;j>=0&&input[j]>temp;j-=dk){
                    //input[j]后移dk位，在input[j]处挖了一个坑
                    input[j+dk] = input[j];
                }
                //填坑
                input[j+dk] = temp;
            }
        }       
    }
    public static void shellSort(int []input,int[]dk){
        for(int i=0;i//执行多个分组插入排序，但最后一个dk，必须是1
            shellInsert(input,dk[i]);
        }
    }
    public static void main(String[] args) throws IOException {
        StreamTokenizer cin = new StreamTokenizer (new BufferedReader(new InputStreamReader(System.in)));
        while(cin.nextToken()!=cin.TT_EOF){
            int n =(int)cin.nval;
            int []input = new int[n];
            for(int i=0;iint)cin.nval;
            }
            int[]dk ={6,5,4,3,1};//{6,5,1}、{4,3,1}都是合理的
            shellSort(input,dk);
            for(int i=0;i" ");
            }
        }
    }
}

该方法实质上是一种分组插入方法。专家们提倡，几乎任何排序工作在开始时都可以用希尔排序，若在实际使用中证明它不够快，再改成快速排序这样更高级的排序算法. 本质上讲，希尔排序算法是直接插入排序算法的一种改进，减少了其复制的次数，速度要快很多。 原因是，当n值很大时数据项每一趟排序需要的个数很少，但数据项的距离很长。当n值减小时每一趟需要和动的数据增多，此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多。希尔排序的时间复杂度与增量序列的选取有关，O(n^2)~O(nlog2n), 算法稳定性：不稳定。

---