数据结构与算法--聊聊散列表查找

前言

在日常的工作中，经常会接触到散列表、MD5算法、哈希表等一些技术，这些都是运用了散列技术。

那么散列表是怎么查找的呢？怎么设计一个散列呢？接下来来聊聊散列表设计的常见手段和怎么解决散列冲突。

1. 散列函数常见手段

算列技术：记录的存储位置和它的关键字之间建立一个确定的对应关系F，使得关键字key对应一个存储位置F(key)。查找时，根据这个对应关系，找到key的映射F(key)，若查找集合中存在这个记录,则必定在F(key)的位置上。

设计散列函数时：

• 存储简单，分布均匀，
• 不适合大范围的查找

接下来，了解一下常见的散列函数设计方法：

1.1 直接定值法：

优点：简单，均匀，不易产生冲突
确定：需要事先知道数据关键字的分布情况，适合查找表小且连续的情况。

例如下图，对0-100岁的人口统计，

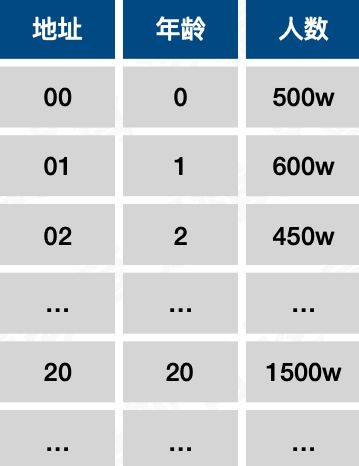
用散列函数存储，F(key) = key，则

假如查找3岁的人口，根据F(3) = 3，直接找到为450W。

假如下图，要对1980年后每年出生的人统计，

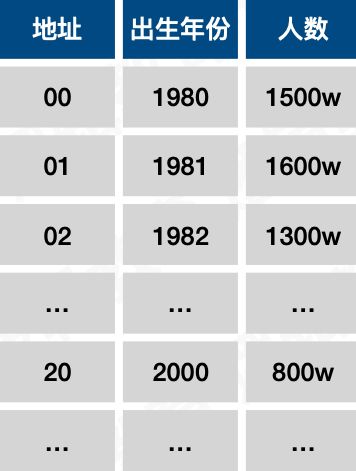
可以设计F(key) = key - 1980。

直接定址法可以设成一个线性函数，
F(key) = a * key + b（其中a和b为常数）。

1.2 数字分析法：

如果关键字是一个位数特别多的数字，比如手机号，找出数字的规律，尽可能利用这些数据来构造冲突几率较低的散列地址。

比如一个地区手机号，前面很多位都相同，不同可能是最后4位数，将这部分作为散列算法的依据。

1.3 平方取中法

取关键字平方后的中间几位作为散列地址。

先通过求关键字的平方值扩大相近数的差别，然后根据表长度取中间的几位数作为散列函数值。又因为一个乘积的中间几位数和乘数的每一位都相关，所以由此产生的散列地址较为均匀。

1.4. 折叠法

折叠法就是将关键字从左到右分割成位数相等的几部分（注意最后一部分位数不够可以稍微短些）。 然后将几部分叠加求和，并按散列表长,取后几位作为散列地址

例如：对数字9876543210进行分割，三位一组，共四组，分别为987、654、321和0。然后对四个数字求和得到1962，最终取和的后三位962作为散列地址。

1.5. 除留余数发

取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。

$f_i(key)=keymodp(p<m)$

2. 散列冲突的解决

2.1 开放定址法

开放定址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存⼊。

$f_i(key)=(f(key)+d_i)Modm；(d_i=1^2,-1^2,2^2,-2^2,...,q^2,-q^2,q<m/2)$

2.2 再散列函数发

事先准备多个散列函数，当一个散列函数冲突时，用另一个散列函数。

$f_i(key)=R{H}_i(key)(i=1,2,3...,k)$

RHi指的是不同的散列函数

2.3. 链地址发

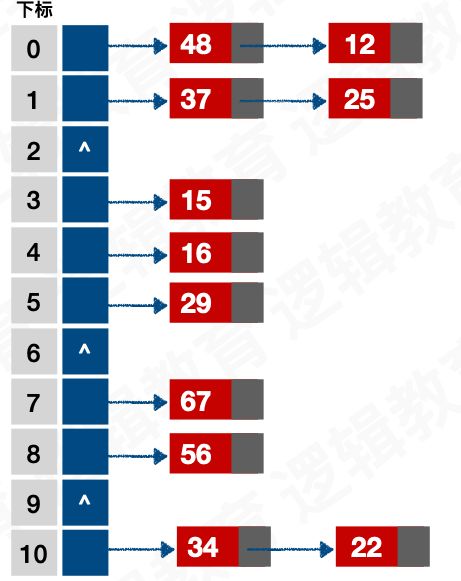
将所有的关键字为同义词的记录存储在一个单链表中，我们称这种为同义词子表，在散列表中只存储同义词子表的头指针。

例如：
关键字集合 { 12,67,56,16,25,37,22,29,15,47,48,34 } 表⻓为12, 我们用散列函数 f ( key ) = key mod 12

则如下存储：

2.4. 公共溢出法

另开一个公共的表存储冲突的数据。基本表没有查找到，就在溢出表中查找。空间浪费严重

3. 散列表实现

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 //存储空间初始分配量
#define SUCCESS 1
#define UNSUCCESS 0

//定义散列表长为数组的长度
#define HASHSIZE 12
#define NULLKEY -32768

typedef struct
{
    //数据元素存储基址，动态分配数组
    int *elem;
    //当前数据元素个数
    int count;
}HashTable;
int m=0; /* 散列表表长，全局变量 */

//1.初始化散列表
Status InitHashTable(HashTable *H)
{
    int i;
    
    //1 设置H.count初始值; 并且开辟m个空间
    m = HASHSIZE;
    H->count = m;
    H->elem = (int *)malloc(m*sizeof(int));
    
    //2 为H.elem[i] 动态数组中的数据置空(-32768)
    for(i = 0; i < m; i++)
        H->elem[i] = NULLKEY;
    
    return OK;
}

//2. 散列函数
int Hash(int key)
{
    //除留余数法
    return key % m;
}

//3. 插入关键字进散列表
void InsertHash(HashTable *H,int key)
{
    
    
    //1. 求散列地址
    int addr = Hash(key);
    
    //2. 如果不为空，则冲突
    while (H->elem[addr] != NULLKEY)
    {
        //开放定址法的线性探测
        addr = (addr+1) % m;
    }
    
    //3. 直到有空位后插入关键字
    H->elem[addr] = key;
}

//4. 散列表查找关键字
Status SearchHash(HashTable H,int key,int *addr)
{
    //1. 求散列地址
    *addr = Hash(key);
    
    //2. 如果不为空，则冲突
    while(H.elem[*addr] != key)
    {
        //3. 开放定址法的线性探测
        *addr = (*addr+1) % m;
        
        //4. H.elem[*addr] 等于初始值或者循环有回到了原点.则表示关键字不存在;
        if (H.elem[*addr] == NULLKEY || *addr == Hash(key))
            //则说明关键字不存在
            return UNSUCCESS;
    }
    
    return SUCCESS;
}