ADVERSARIAL EXAMPLES IN THE PHYSICAL WORLD
文章目录
- 概
- 主要内容
- least likely class adv.
- 实验1 l.l.c. adv.的效用
- 实验二
Alexey Kurakin, Ian J. Goodfellow, Samy Bengio, ADVERSARIAL EXAMPLES IN THE PHYSICAL WORLD
概
有很多种方法能够生成对抗样本(adversarial samples), 但是真实世界中是否存在这样的对抗样本呢?
主要内容
least likely class adv.
假设 X X X为图像(各元素取值为 [ 0 , 255 ] [0,255] [0,255]), y t r u e y_{true} ytrue为其标签, f ( X ) f(X) f(X)为一模型, 其输出是一个概率向量, 定义
y L L : = arg min i { f ( X ) i } , y_{LL}:=\arg \min_i \{f(X)_i\}, yLL:=argimin{f(X)i},
故本文的生成adversarial samples的方法是最小化
J ( X , y L L ) : = − log f ( X ) y L L , J(X,y_{LL}):=-\log f(X)_{y_{LL}}, J(X,yLL):=−logf(X)yLL,
则
X 0 a d v = X , X N + 1 a d v = C l i p X , ϵ { X N a d v − α s i g n ( X N a d v , y L L ) } , X_0^{adv}=X,\quad X_{N+1}^{adv}=Clip_{X,\epsilon} \{X_N^{adv} - \alpha \mathrm{sign}(X_N^{adv},y_{LL})\}, X0adv=X,XN+1adv=ClipX,ϵ{XNadv−αsign(XNadv,yLL)},
其中
C l i p X , ϵ ( X ′ ) : = min { 255 , X + ϵ , max { 0 , X − ϵ , X ′ } } , Clip_{X,\epsilon}(X'):=\min \{ 255,X+\epsilon, \max\{0,X-\epsilon, X'\} \}, ClipX,ϵ(X′):=min{255,X+ϵ,max{0,X−ϵ,X′}},
即使得 X ′ X' X′落入 [ 0 , 255 ] [0,255] [0,255]内且, ∥ X − X ′ ∥ ∞ ≤ ϵ \|X-X'\|_{\infty} \le \epsilon ∥X−X′∥∞≤ϵ.
实验1 l.l.c. adv.的效用
对l.l.c. adv. 和 fgsm, ifgsm进行了比较
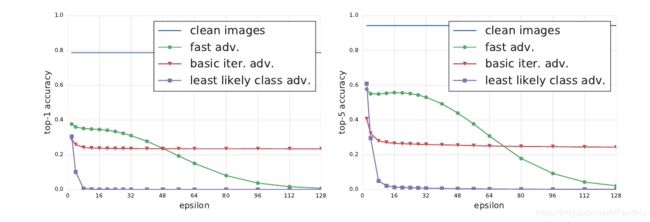
实验二
为了探究真实世界是否也存在这样的对抗样本, 作者将图片进行如下操作:
- 打印 ( a )
- 用手机将打印的照片拍照 ( b )
- 对照片进行裁剪找出所需的部分 ( c )
可以把这种操作看成一个变换 T : X → T ( X ) T:X \rightarrow T(X) T:X→T(X), 如果真实世界中也存在对抗样本, 那么原本的adversarial samples 在经过这个变换之后很有可能也具有对抗的性质, 事实上, 实验显示的确, 虽然其对抗的程度有些许下降.
作者构建了一个指标(重构率)来衡量:
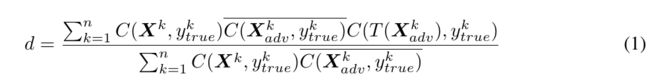
其中

C ( X , y ) ‾ = 1 − C ( X , y ) \overline{C(X,y)}=1-C(X,y) C(X,y)=1−C(X,y).
d d d表示经过变换 T T T后, adversarial samples 变成普通样本(即不被误判)的比例, 实验显示, 在实验一中表现出色的l.l.c. adv., d d d反而比较高, 作者猜测这是因为这个方法产生的扰动比较精细, 经过 T T T变换后, 这部分扰动就容易被抵消.
