Parabola（抛物线）
找这篇介绍抛物线的文章是为了我设计一个轨迹所用，人越往上走，这最基本的东西都忘了，翻译了一点，因为我只用到了翻译的这些，各位如果有需求，就自行翻译。英文好的，就自己读英文。（谷歌翻译是个好东西，英文复制上去，翻译的基本上就八九不离十了，再加上自己的判断，改改就可以了！）
抛物线（复数“抛物线”;格雷1997，第45页）是平面中与给定线
（圆锥截面准线）等距离的所有点的集合和不在线上的给定点
（焦点）。 因此，参数（即，准线和焦点之间的距离）由下式给出
，其中
是从顶点到准线或焦点的距离。 通过使抛物线绕其对称轴旋转而获得的旋转表面被称为抛物面。
Menaechmus研究了抛物线，试图实现立方体复制。 Menaechmus通过找到两个抛物线
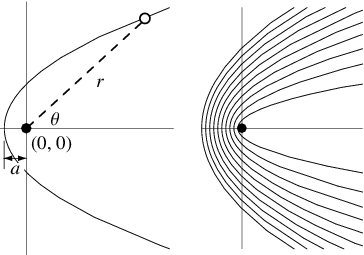
和
的交点解决了这个问题。 Euclid写了关于抛物线的信息，Apollonius给它现在的名字。 帕斯卡尔认为抛物线是一个圆的投影，伽利略表明落在均匀重力下的抛射物遵循抛物线路径。 格雷戈里和牛顿考虑了抛物线的反射焦散曲线特性，它将平行光线带到焦点上（MacTutor Archive），如上图所示。
对于在（0,0）处具有顶点的右侧抛物线，笛卡尔坐标系中的方程为
 |
(1) |
 |
(2) |
 |
(3) |
 |
(4) |
The quantity 
is known as the latus rectum. If the vertex is at 
instead of (0, 0), the equation of the parabola is
 |
(5) |
If the parabola instead opens upwards, its equation is
 |
(6) |
Three points uniquely determine one parabola with directrix parallel to the 
-axis and one with directrix parallel to the 
-axis. If these parabolas pass through the three points 
, 
, and 
, they are given by equations
 |
(7) |
and
 |
(8) |
In polar coordinates, the equation of a parabola with parameter 
and center (0, 0) is given by
 |
(9) |
(left figure). The equivalence with the Cartesian form can be seen by setting up a coordinate system 
and plugging in 
and 
to obtain
 |
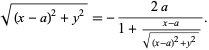(10) |
Expanding and collecting terms,
 |
(11) |
so solving for 
gives (◇). A set of confocal parabolas is shown in the figure on the right.
In pedal coordinates with the pedal point at the focus, the equation is
 |
(12) |
The parabola can be written parametrically as
 |
 |
 |
(13) |
 |
 |
 |
(14) |
or
 |
 |
 |
(15) |
 |
 |
 |
(16) |
A segment of a parabola is a Lissajous curve.
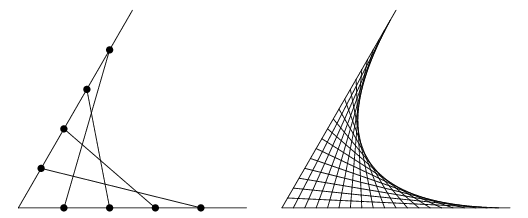
A parabola may be generated as the envelope of two concurrent line segments by connecting opposite points on the two lines (Wells 1991).
In the above figure, the lines 
, 
, and 
are tangent to the parabola at points 
, 
, and 
, respectively. Then 
(Wells 1991). Moreover, the circumcircle of 
passes through the focus 
(Honsberger 1995, p. 47). In addition, the foot of the perpendicular to a tangent to a parabola from the focus always lies on the tangent at the vertex (Honsberger 1995, p. 48).
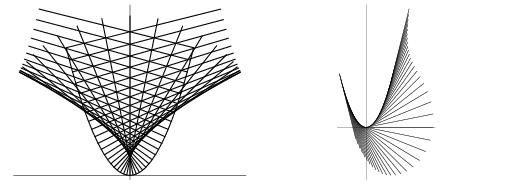
Given an arbitrary point 
located "outside" a parabola, the tangent or tangents to the parabola through 
can be constructed by drawing the circle having 
as a diameter, where 
is the focus. Then locate the points 
and 
at which the circle cuts the vertical tangent through 
. The points 
and 
(which can collapse to a single point in the degenerate case) are then the points of tangency of the lines 
and 
and the parabola (Wells 1991).
The curvature, arc length, and tangential angle are
 |
 |
 |
(17) |
 |
 |
 |
(18) |
 |
 |
 |
(19) |
The tangent vector of the parabola is
 |
 |
 |
(20) |
 |
 |
 |
(21) |
The plots below show the normal and tangent vectors to a parabola.
SEE ALSO:Conic Section, Ellipse, Hyperbola, Parabola Catacaustic, Parabola Evolute, Parabola Inverse Curve, Parabola Involute, Parabola Negative Pedal Curve, Parabola Pedal Curve, Paraboloid, Quadratic Curve, Reflection Property, Tschirnhausen Cubic Pedal Curve, Welch Apodization FunctionREFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 198 and 222-223, 1987.
Casey, J. "The Parabola." Ch. 5 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 173-200, 1893.
Coxeter, H. S. M. "Conics." §8.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 115-119, 1969.
Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.
Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 4, 1999.
Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 47-48, 1995.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 67-72, 1972.
Lockwood, E. H. "The Parabola." Ch. 1 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 2-12, 1967.
Loomis, E. S. "The Parabola." §2.5 in The Pythagorean Proposition: Its Demonstrations Analyzed and Classified and Bibliography of Sources for Data of the Four Kinds of "Proofs," 2nd ed. Reston, VA: National Council of Teachers of Mathematics, pp. 25-28, 1968.
MacTutor History of Mathematics Archive. "Parabola." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html.
Pappas, T. "The Parabolic Ceiling of the Capitol." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 22-23, 1989.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 169-172, 1991.
Yates, R. C. "Conics." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 36-56, 1952.
CITE THIS AS:
Weisstein, Eric W. "Parabola." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Parabola.html