回声状态网络(ESN)教程
回声状态网络(ESN)教程
基础概念
回声状态网络(Echo State Network)提出于2001年,曾经是研究的热点,但近年来随着RNN,LSTM与其它一些变种的网络的出现,现在研究比较少了,但是其在时间序列预测上还有着很不错的应用。传统的MLP网络的隐层是一层层的全连接的神经元,而ESN引入了一个储备池计算模式来替代原始的隐层,这个储备池是什么呢?先来看下下图:
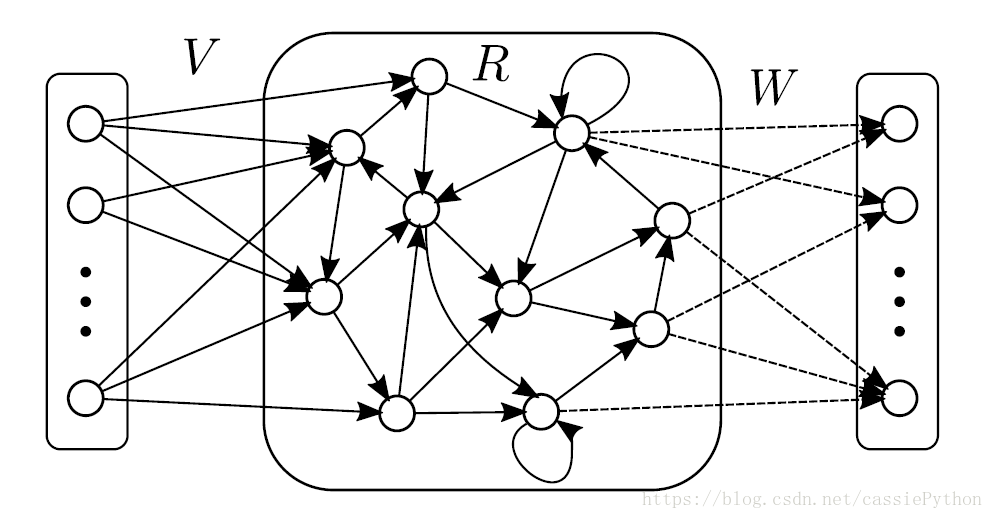
网络结构依次是输入层,储备池和输出层,所谓的储备池就是中间的部分。这个储备池的特点是: (1)储备池中神经元的连接状态是随机的,即神经元之间是否建立连接并不是我们人工确定的;(2)储备池中的连接权重是固定的,不像传统的MLP网络使用梯度下降进行权重的更新。这样做的好处是:(1)大大降低了训练的计算量;(2)一定程度上避免了梯度下降的优化算法中出现的局部极小情况;(3)此外,在很多问题上确实有着不错的建模能力。ESN的基本思想就是由储备池生成一个随输入不断变化的复杂动态空间,当这个状态空间足够复杂时,就可以利用这些内部状态, 线性地组合处所需要的对应输出~(实际上就是传统的MLP拟合的能力)。那么,到底是如何训练这个网络的呢?不要着急,我们先来对ESN 做一些数学符号的定义。
数学定义
假设这个回声状态网络有 N N 个中间节点,即储备池中的神经元个数为 N N ,输入层和输出层神经元个数都为 D D 。用 u(t)∈RD,x(t)∈RN,f(t)∈RD u ( t ) ∈ R D , x ( t ) ∈ R N , f ( t ) ∈ R D 分别表示t时刻的输入,网络状态(储备池的状态)和输出; V∈RN×D,R∈RN×N,W∈RD×N V ∈ R N × D , R ∈ R N × N , W ∈ R D × N 分别表示输入权重、中间权值及输出权重矩阵, tanh(⋅) t a n h ( ⋅ ) 为激活函数。注意,有些文献会把 V V 定义为 Win W i n , W W
定义为 Wout W o u t , R R 定义为 W W 。
则储备池的状态更新方式以及网络的输出为:
构造过程
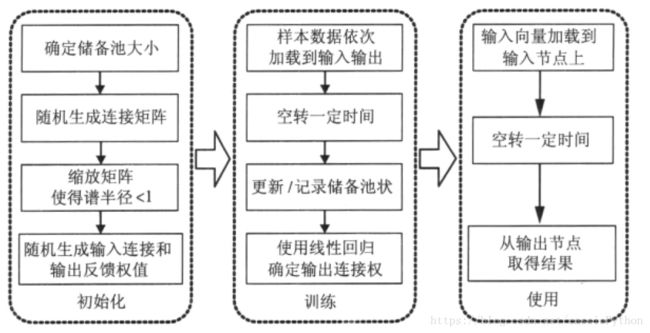
首先我们来看下ESN的构造过程:初始化,训练以及使用(测试),如下图所示。
首先进行初始化操作,在这步里,我们先确定储备池的大小,即神经元的个数。与传统的MLP相同,节点数越多,拟合能力越强。由于ESN仅仅通过调整输出权值(即图1中的 W W ,我们最终就是利用储备池的状态信息来确定这个 W W )来线性拟合输出结果,所以一般ESN需要远大于一般神经网络的节点规模。
接下来是随机生成连接矩阵,这个矩阵表示了哪些神经元之间是有连接的,以及连接的方向和权值,实际上就是有向图的矩阵表示~(即图1中的 R R )。接下来的缩放矩阵实际上就是归一化的操作,有些时候我们会直接使用一个缩放因子,使用该缩放因子乘以原始的随机生成的矩阵,相比于使用特征值来缩放更加快速,但是很大程度上也丧失了精度。为什么要进行这个操作呢?原因和我们在初始化一些神经网络的权值时是类似的,对于这些神经网络,我们通常会将权重初始化为0-1之间(或着-1至1),有两个原因:~(1)受激活函数的影响,比如图3所示的 sigmoid s i g m o i d 和 tanh t a n h 激活函数,在0与1之间区分度比较大,但是大于1之后,激活值变化不大;~(2)我们对激活函数求导,可以看出在大于1时,图像比较平坦,其导数接近于0,由此在计算梯度时会导致梯度过小,无法顺利实现权重的更新。对于ESN我们不使用梯度来更新权值,主要是第一点的问题。最后随机生成输入权值 V V 和输出权值 W W 。
这些参数会影响到网络短期记忆时间的长短。输入权值越小而内部矩阵的谱半径越接近1,网络短期记忆时间越长。但是,增强记忆能力的同时,这种操作也造成了网络对“快速变化”系统的建模能力下降。
第二步进行训练。值得注意的是这个“空转”过程,实际上就是初始化储备池的状态。为什么要进行这个操作呢?因为储备池的内部连接是随机的,最开始的输入序列得到储备池状态的噪声会比较大,所以会先使用一些数据来初始化储备池的状态,从而降低噪声的影响。对于使用线性回归确定输出权值,在下一部分我们来一起进行推导。
数学推导
我们来对前面所说的输出权值进行求解。问题如下:这里假定对输出权重 W W 做了2范数正则,正则化系数为 λ λ 。记网络状态矩阵为 X X ,输出序列矩阵
为 Y Y ,请写出输出权重 W W 的计算公式。
首先我们要优化的目标是:
求解非常简单,只需要对其求导,令其导数为0,解出 W W 即可,实际上就是最小二乘法求解,可得:
进一步说,就是岭回归(带2范数惩罚项的最小二乘回归)。
考虑一个等价的问题:考虑概率情况, y(t)=f(t)+ε y ( t ) = f ( t ) + ε ,其中 ε∼N(0,β−1I) ε ∼ N ( 0 , β − 1 I ) ,
且对于 Wi W i 的分布有 Wi∼N(0,α−1I) W i ∼ N ( 0 , α − 1 I ) 。证明最大化后验 p(Wi|X,Yi) p ( W i | X , Y i ) 得到的输出权重与第1问中最小二乘法得到的输出权重等价。
最大化后验,即:
由于分母与 W W 无关,所以可以省略,由此上式等价于:
假设训练样本数为 L L ,则上式等价于:
加上对数处理后,上式可变为:
由题目中的条件可知: Yi−WiXi∼N(0,β−1I) Y i − W i X i ∼ N ( 0 , β − 1 I ) ,所以上式
可写作:
展开上式,即等价于:
将负号去掉,则上式变为:
使用矩阵的形式来表示,可得:
进一步地等价于:
我们令 λ=αβ λ = α β ,即可得到最终的式子:
哈,可以看到与公式1是相同的,由此得证。
Matlab代码实现
这里给出Matlab代码的实现,代码来源于http://minds.jacobs-university.de/mantas:
% A minimalistic Echo State Networks demo with Mackey-Glass (delay 17) data
% in "plain" Matlab.
% by Mantas Lukosevicius 2012
% http://minds.jacobs-university.de/mantas
% load the data
trainLen = 3000;
testLen = 1000;
initLen = 100;
data = load('MackeyGlass-t17.txt');
% plot some of it
% figure(10);
% plot(data(1:1000));
% title('A sample of data');
% generate the ESN reservoir
inSize = 1; outSize = 1;
resSize = 1000;
a = 0.3; % leaking rate
%rand( 'seed', 42 );
Win = (rand(resSize,1+inSize)-0.5) .* 1;
W = rand(resSize,resSize)-0.5;
% Option 1 - direct scaling (quick&dirty, reservoir-specific):
% W = W .* 0.13;
% Option 2 - normalizing and setting spectral radius (correct, slower):
disp 'Computing spectral radius...';
opt.disp = 0;
rhoW = abs(eigs(W,1,'LM',opt));
disp 'done.'
W = W .* ( 1.25 /rhoW);
% allocated memory for the design (collected states) matrix
X = zeros(1+inSize+resSize,trainLen-initLen);
% set the corresponding target matrix directly
Yt = data(initLen+2:trainLen+1)';
% run the reservoir with the data and collect X
x = zeros(resSize,1);
for t = 1:trainLen
u = data(t);
x = (1-a)*x + a*tanh( Win*[1;u] + W*x );
if t > initLen
X(:,t-initLen) = [1;u;x];
end
end
% train the output
reg = 1e-8; % regularization coefficient
X_T = X';
% Wout = Yt*X_T * inv(X*X_T + reg*eye(1+inSize+resSize));
Wout = Yt*X_T / (X*X_T + reg*eye(1+inSize+resSize));
% Wout = Yt*pinv(X);
% run the trained ESN in a generative mode. no need to initialize here,
% because x is initialized with training data and we continue from there.
Y = zeros(outSize,testLen);
u = data(trainLen+1);
for t = 1:testLen
x = (1-a)*x + a*tanh( Win*[1;u] + W*x );
y = Wout*[1;u;x];
Y(:,t) = y;
% generative mode:
u = y;
% this would be a predictive mode:
%u = data(trainLen+t+1);
end
errorLen = 1000;
mse = sum((data(trainLen+2:trainLen+errorLen+1)'-Y(1,1:errorLen)).^2)./errorLen;
disp( ['MSE = ', num2str( mse )] );
% plot some signals
figure(1);
plot( data(trainLen+2:trainLen+testLen+1), 'color', [0,0.75,0] );
hold on;
plot( Y', 'b' );
hold off;
axis tight;
title('Target and generated signals y(n) starting at n=0');
legend('Target signal', 'Free-running predicted signal');
figure(2);
plot( X(1:20,1:200)' );
title('Some reservoir activations x(n)');
figure(3);
bar( Wout' )
title('Output weights W^{out}');
后记
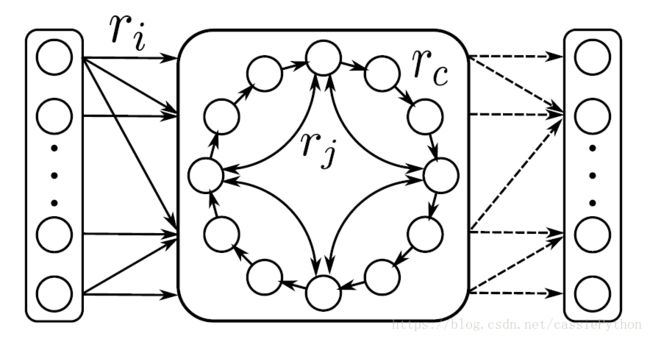
确定性跳跃循环状态网络(CRJ)是ESN的一个变种,如图所示:
在下一节我们会基于前面的ESN的代码一起来实现一个CRJ。