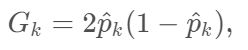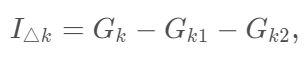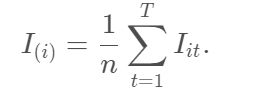高维数据中特征筛选方法的思考总结——多变量分析筛选法
前言:之前的文章(高维数据中特征筛选方法的思考总结——单变量分析筛选法)中,对单变量分析筛选变量进行了初步考量,本文将进一步总结多变量分析筛选法。由于本文多处摘录网上的博客,只是进行了归纳整理,因此笔者将本文定性为转载类(转载请注明出处:https://blog.csdn.net/fjsd155/article/details/93754257)。
多变量分析方法根据建模特点可以分为线性降维和非线性降维。线性降维主要是 LASSO 和 PLS。非线性降维包括:XGBoost(GBDT的高效实现)、Random Forest 等。其实个人感觉CNN应该也是可以进行非线性降维的(但是目前CNN处理“非序列数据”并没有优势,笔者有个预处理的设想,准备尝试一下拓宽CNN的适用范围)。另外SVM这种强大的机器学习方法,似乎只能用来建模而不能筛选特征。
LASSO和PLS都是线性模型的降维方法,也就是说,这两种方法甚至包括上述单变量降维的方法,最终筛选的变量都是为了建立线性模型而准备的,而不能孵育出非线性模型(如存在交互作用的模型、复杂的SVM模型、决策树类模型以及复杂的神经网络模型)。非线性模型的生物学解释性很差(黑箱模型),一般不推荐使用。但是若强行想构建非线性模型,则仅采用上述线性降维的方法是不够理想的,需要采用非线性降维。
注意一个问题的存在:我们筛选特征往往基于训练数据(选择超参数或者最终建模常常会根据交叉验证,但是变量的筛选却常常只是基于训练集)。在训练数据中,变量的贡献程度越大,并不意味着这个变量越有价值。可能某些变量在模型中表现很普通,但是始终十分稳定(经得起考验);而有些变量在训练数据中表现很好,但外推性却较弱,表现波动大。因此变量的选择有必要综合训练数据和验证数据(如综合CV或Bootstrapping筛选变量)。最后再由独立测试数据进行检验。
筛选特征及建模的科学观念:模型的可重复性(多批数据)>大样本建模>模型的准确性。有人提出(貌似是范剑青老师等人提出),“针对一个统计方法,统计准确性、模型可解释性和计算复杂性是衡量其好坏的三个重要指标。”
(下面部分内容参考自:
一些变量筛选方法——1、综述
一些变量筛选方法——2、《An Introduction to Statistical Learning with R》上的数据降维方法
一些变量筛选方法——3、部分其它变量筛选方法)
刚刚从线性与否的角度对降维方法进行了分类概述。另外,An Introduction to Statistical Learning with R 这本书中将筛选变量的方法分为:子集选择法(Subset Selection)、系数压缩法(Shrinkage)、映射降维法(Dimension Reduction)。
子集选择法
子集选择法分为最优子集选择、逐步筛选法等,这部分方法依赖于下述模型评判指标:
- Mallows 提出运用Cp去评估一个以普通最小二乘法(Ordinary Least Square或OLS)为假设的线性回归模型的优良性,从而用于模型选择。
- 日本学者 Akaike 在1974年基于极大似然方法提出了AIC准则,它建立在熵的概念基础上,可以权衡所估计模型的复杂度和此模型拟合数据的优良性。
- Schwarz 在Bayes方法的基础上提出BIC准则。与AIC相比,BIC加强了惩罚力度,考虑了样本量,从而在选择变量进入模型上更加谨慎。
- Seymour Geisser 提出了交叉验证法(Cross validation),利用交叉验证结合最小平方误差的方法,是一种在没有任何前提假定的情况下直接进行参数估计的变量选择方法。
此外,还可以使用Adjusted R2进行评价来选择特征子集。这些指标的具体含义和使用方法,可参照An Introduction to Statistical Learning with R 或 一些变量筛选方法——2、《An Introduction to Statistical Learning with R》上的数据降维方法。
最优子集法(Best Subset Selection):其思想是将所有的特征组合都进行建模,然后选择最优的模型(最优的判断依据都是前面叙述的几种指标)。特点是能够找到全局最优但是计算量较大。
逐步筛选法(Stepwise Selection)分为向前逐步回归与向后逐步回归。其主要思想是:每一次迭代都只能沿着上一次迭代的方向继续进行。向前逐步回归是指初始模型只有常数项,然后逐渐添加变量;向后逐步回归是指初始模型包含了所有变量,然后逐渐删除变量。特点是仅关注局部最优(贪心策略)难以保证全局最优(注:向前与向后逐步回归筛选出的变量可能不一样,但其思想完全一样。)
系数压缩法
系数压缩法主要指LASSO。岭回归只能实现系数压缩而不能降维,但是可以通过合理的调参,将系数压缩后对系数进行排序,从而实现降维(但既然LASSO已经还不错了,没必要强行使用岭回归降维)。
LASSO可参考博客:LASSO回归
映射降维法
映射降维法主要指的是PLS。另外,PCR(主元回归法)是进行主成分分析(PCA)后,选取前几个主成分进行建模,但实际上建模的效果很一般;PLS是基于PCA的思想,结合回归建模、典型关联分析(CCA)以及拟合残差(带一点Gradient Boost)等各家思想,所孕育出的一种建模分析和降维方法。
PLS可参考博客:偏最小二乘法 Partial Least Squares
其他不错的方法
除了上述三大类方法,树结构的方法以及Boosting类的方法也是比较有效的,如:Random Forest、XGBoost(GBDT的高效实现)等。此外,Fan和Li 结合L0与L1范数提出的SCAD (Smoothly Clipped Absolute Deviation);Fan 提出的SIS(Sure Independence Screening)等。
Random Forest
随机森林模型本身是用于预测的模型,但在预测过程中,可以对变量重要性进行排序,然后通过这种排序来进行变量筛选。
变量重要性评判用Gini指数为标准,针对一棵树中的每个节点 k,我们都可以计算一个Gini指数:
其中
表示样本在节点 k 属于任意一类的概率估计值。
和
分别表示
产生的子节点。针对森林中的每棵树,都用上述的标准来递归产生,最终随机抽取样本和变量,产生森林,假设森林共产生 T 棵树。
森林中,如果变量
在第 t 棵树中出现 M 次,则变量
在第 t 棵树的重要性为:
则
在整个森林中的变量重要性为:
最终我们根据变量重要性来选择变量,选择的个数可以用SIS中的方法,选取n−1 或n/logn 个。
XGBoost
GBDT的建模过程是,一步步拟合残差,那么在一步步的拟合的过程中,也便是变量选择的过程(从一定程度上实现了变量的筛选)(这种逐步拟合残差的思想的方法还有PLS)。XGBoost是GBDT的高效实现方法。
GBDT的介绍可参考:GBDT
XGBoost 的介绍可参考:XGBoost
SCAD
与岭回归相比,SCAD降低了模型的预测方差,与此同时与LASSO相比,SCAD又缩小了参数估计的偏差,因而受到了广泛的关注。L0方法只会进行变量筛选,不会进行压缩,L1(LASSO)既会进行变量筛选,也会对系数继续一定的调整。而SCAD可以从图中很明显的其结合了两种方法,对系数较大的变量不进行惩罚,对系数较少的进行压缩或者删去,因此这种方法既可以筛选变量,也有着Oracle的性质。SCAD虽然有相应的迭代算法,但是由于其复杂度高,所以计算速度相对较慢。
SCAD的产生,有点借鉴Elastic Net。
SIS
当遇到超高维数据,即维数P无穷大时,上述的算法会出现问题。针对这类超高维问题,Fan等人提出了SIS的方法。
针对线性回归模型(2),按照SIS的思想,首先Y为中心化向量,计算Y与每一个自变量
的相关系数,记为
其中
,若
越大,说明
与Y 相关性越强。所以,可以根据
的大小来进行变量选择。对任意的
,对
进行从大到小排序,然后取其一个子集
其中,n是样本数,
是
的整数部分,进而保证了
,与之对应的自变量则入选模型。如果觉得选择
不便于确定,可以选择 n-1 或n/logn。
而关于相关系数,可以选用自己认为合适的。本文后面的模拟选用传统的Pearson相关系数,以及近几年比较火的可用于检验独立的无参数假设的距离相关性(Distance Covariance)(见:一些变量筛选方法——3、部分其它变量筛选方法)。
严格来说,SIS 属于单变量分析方法。
另外,SIS有一些衍生版本,如DC-SIS及Qa-SIS等,其中Qa-SIS好像是可以处理非线性问题的(据说还是“异方差”)。
PDAS
原始对偶激活集算法(Primal Dual Active Set,PDAS)是一个非常新的方法,但做的事情是最优子集选择的事情。其主要思想是引入激活集,对所有的 β 进行批量迭代更新。这个方法的优势在于,可以处理超高维数据(上万维),而最优子集选择一旦超过了50维,基本就完全没办法进行运算。后面我们也将采用PDAS来进行模拟。
PDAS的介绍可参考:一些变量筛选方法——3、部分其它变量筛选方法
另外,有人总结了7种降维方法(七种降维方法):
- 缺失值比率 (Missing Values Ratio) ;
- 低方差滤波 (Low Variance Filter) ;
- 高相关滤波 (High Correlation Filter);
- 随机森林/组合树 (Random Forests);
- 主成分分析 (PCA);
- 反向特征消除 (Backward Feature Elimination);
- 前向特征构造 (Forward Feature Construction)。
本文的总结其实基本上都包含了这些内容。
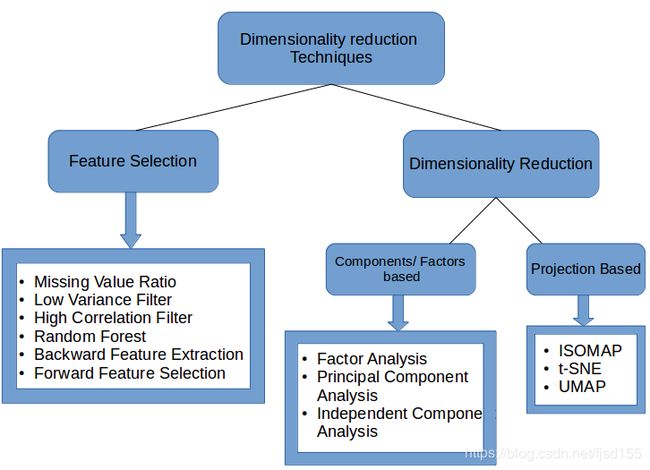
也有人总结了12种降维方法(在以上7种方法基础上加了5种)(来源:Analytics Vidhya:The Ultimate Guide to 12 Dimensionality Reduction Techniques (with Python codes),也可参考:12种降维方法终极指南(含Python代码)):
- 缺失值比率:如果数据集的缺失值太多,我们可以用这种方法减少变量数。
- 低方差滤波器:这个方法可以从数据集中识别和删除常量变量,方差小的变量对目标变量影响不大,所以可以放心删去。
- 高相关滤波器:具有高相关性的一对变量会增加数据集中的多重共线性,所以用这种方法删去其中一个是有必要的。
- 随机森林:这是最常用的降维方法之一,它会明确算出数据集中每个特征的重要性。
- 向后特征消除:耗时较久,计算成本也都很高,所以只适用于输入变量较少的数据集。
- 前向特征选择:思路类似于“向后特征消除”。
- 因子分析:这种方法适合数据集中存在高度相关的变量集的情况。
- 主成分分析(PCA):这是处理线性数据最广泛使用的技术之一。
- 独立分量分析(ICA):我们可以用ICA将数据转换为独立的分量,使用更少的分量来描述数据。
- 基于投影的方法:ISOMAP适合非线性数据处理。
- t分布式随机邻域嵌入(t-SNE):也适合非线性数据处理,相较上一种方法,这种方法的可视化更直接。
- UMAP:用于高维数据,与t-SNE相比,这种方法速度更快。
之后有空可以再总结下 t-SNE(无监督降维方法,主要用于高维度数据的降维可视化)。
另外,scikit-learn机器学习工具包的官网也有一些特征筛选的方法介绍,有博客基于此进行了介绍(原文:http://dataunion.org/14072.html,但是好像原文访问不了了,可以看看转载的博客,比如:几种常用的特征选择方法,或 干货:结合Scikit-learn介绍几种常用的特征选择方法 )。
除了这些,还有一些方法也值得一试,如:随机投影(Random Projections),非负矩阵分解(N0n-negative Matrix Factorization),自动编码(Auto-encoders),卡方检测与信息增益(Chi-square and information gain), 多维标定(Multidimensional Scaling), 相关性分析(Coorespondence Analysis),聚类(Clustering)以及贝叶斯模型(Bayesian Models)。
基于聚类的方法,可以参考:
特征筛选(变量聚类proc varclus)
聚类特征变量选取、聚类算法与效果评价简述
特征选择(二)-聚类变换
还有互信息法、模拟退火法以及一些组合策略等,之后再了解一下。参考:
特征选择(2):特征选择:方差选择法、卡方检验、互信息法、递归特征消除、L1范数
模拟退火筛选变量
特征选择的策略--数据相关性(皮尔逊系数)与gini或者信息熵的的结合
特征选择之基于相关性的特征选择(CFS)
自编码器也是不错的无监督降维方法,是一种神经网络,之后可以研究下。
各种方法的对比评测及代码示例
这部分内容可以参考:
一些变量筛选方法——4、模拟实验
一些变量筛选方法——5、真实数据与总结
一些变量筛选方法——6、代码
参考资料
一些变量筛选方法——1、综述
一些变量筛选方法——2、《An Introduction to Statistical Learning with R》上的数据降维方法
一些变量筛选方法——3、部分其它变量筛选方法
一些变量筛选方法——4、模拟实验
一些变量筛选方法——5、真实数据与总结
一些变量筛选方法——6、代码
LASSO回归
偏最小二乘法 Partial Least Squares
GBDT
XGBoost
七种降维方法
The Ultimate Guide to 12 Dimensionality Reduction Techniques (with Python codes)
Comprehensive Guide on t-SNE algorithm with implementation in R & Python
12种降维方法终极指南(含Python代码)
特征筛选(变量聚类proc varclus)
聚类特征变量选取、聚类算法与效果评价简述
特征选择(一)-维数问题与类内距离
特征选择(二)-聚类变换