154. Find Minimum in Rotated Sorted Array II

154是 153的升级版本。

题目理解

输入：一个按升序排序的数组nums，但是这个数组在某个位置被旋转了。(例如., 原始数组是[0,1,2,4,5,6,7]，旋转后就变成 [4,5,6,7,0,1,2])。注意：这个数组可能包含重复元素。
输出：这个数组的最小值
要求：O(lgn)时间复杂度
示例1
Input: [3,4,5,1,2]
Output: 1

示例2
Input: [2,2,2,0,1]
Output: 0

示例3

Input: [2,2,2,2,2]
Output: 2

二分+分治

这种思路完全可以按照之前在153的分析实现。在上一个版本的分析中，我们只有在需要判断一个子数组是否有序的时候使用大小比较：nums[l] 所以代码是一样的。

只有二分

原文链接

在标准的二分搜索中会用中间元素与目标值比较：nums[pivot]>target。在这里，中间元素与右边界元素比较：nums[pivot]与nums[high]。
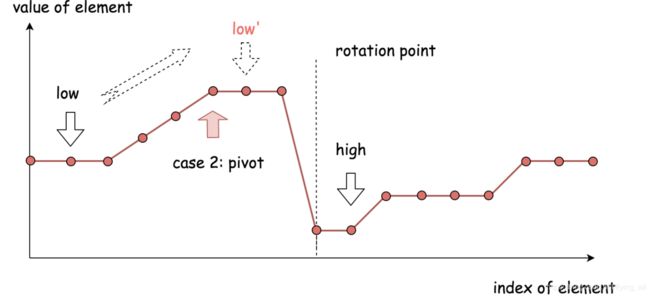
情况一：nums[pivot]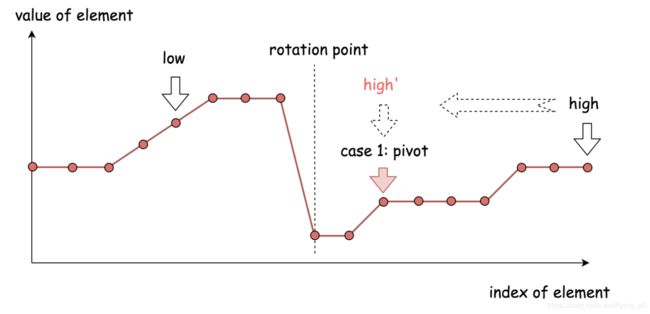

这个时候子数组从pivot到high是一个有序数组，最小元素出现在左侧子数组中。同时，当前中间元素也可能是最小值元素。所以更新high=pivot。

情况二：nums[pivot]>nums[high]

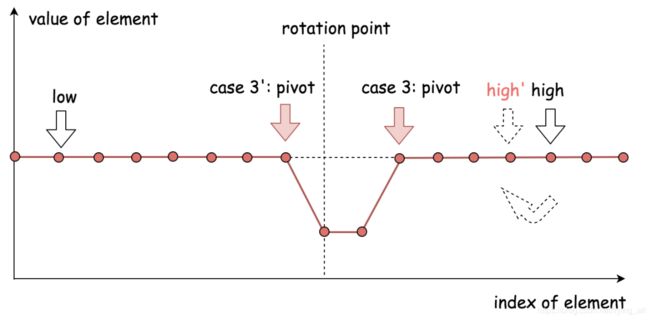
nums[pivot]和最右边元素不在同一侧。一个数组从高到低，一定经历了最小元素。最小元素在右侧子数组中。

情况三：nums[pivot] = nums[high]

如果是图中case3的情况，最小元素在中间元素的左边。如果是图中case3’的情况，则最小元素在中间元素的右边。这个时候缩小右边界的范围：high=high-1。

class Solution {
    public int findMin(int[] nums) {
        int l = 0 ,r = nums.length-1;
        if(nums[r]>nums[l]) return nums[l];
        while(l<=r){
            int mid = l+((r-l)>>1);
            if(nums[mid]<nums[r]){
                r = mid;
            }else if(nums[mid]>nums[r]){
                l = mid+1;
            }else{
                r = r-1;
            }
        }
        return nums[l];
    }  
}