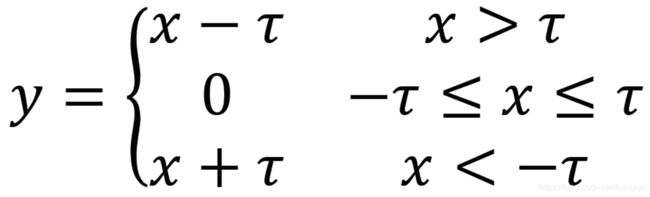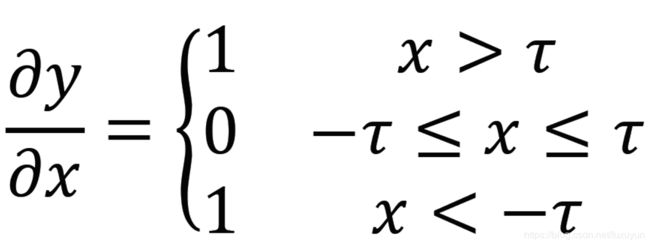深度残差收缩网络：深度注意力机制下的软阈值化

深度残差网络（deep residual learning, ResNet）获得了2016年CVPR会议的最佳论文奖，截至目前，在谷歌学术上的引用次数已经达到了37225次。

深度残差收缩网络（deep residual shrinkage network）是深度残差网络的一种新的升级版本，其实是深度残差网络、注意力机制（参照Squeeze-and-Excitation Network，SENet）和软阈值化的深度集成。

在一定程度上，深度残差收缩网络的工作原理，可以理解为：通过注意力机制注意到不重要的特征，然后通过软阈值化将它们置为零；或者说，通过注意力机制注意到重要的特征，将它们保留下来，从而加强深度神经网络从含噪声信号中提取有用特征的能力。

1.为什么要提出深度残差收缩网络呢？

首先，在对样本进行分类的时候，样本中不可避免地会有一些噪声，就像高斯噪声、粉色噪声、拉普拉斯噪声等。更广义地讲，样本中很可能包含着与当前分类任务无关的信息，这些信息也可以理解为噪声。这些噪声可能会对分类效果产生不利的影响。（软阈值化是许多信号降噪算法中的一个关键步骤）

举例来说，在马路边聊天的时候，聊天的声音里就可能会混杂车辆的鸣笛声、车轮声等等。当对这些声音信号进行语音识别的时候，识别效果不可避免地会受到鸣笛声、车轮声的影响。从深度学习的角度来讲，这些鸣笛声、车轮声所对应的特征，就应该在深度神经网络内部被删除掉，以避免对语音识别的效果造成影响。

其次，即使是同一个样本集，各个样本的噪声量也往往是不同的。（这和注意力机制有相通之处；以一个图像样本集为例，各张图片中目标物体所在的位置可能是不同的；注意力机制可以针对每一张图片，注意到目标物体所在的位置）

例如，当训练猫狗分类器的时候，对于标签为“狗”的5张图像，第1张图像可能同时包含着狗和老鼠，第2张图像可能同时包含着狗和鹅，第3张图像可能同时包含着狗和鸡，第4张图像可能同时包含着狗和驴，第5张图像可能同时包含着狗和鸭子。我们在训练猫狗分类器的时候，就不可避免地会受到老鼠、鹅、鸡、驴和鸭子等无关物体的干扰，造成分类准确率下降。如果我们能够注意到这些无关的老鼠、鹅、鸡、驴和鸭子，将它们所对应的特征删除掉，就有可能提高猫狗分类器的准确率。

2.软阈值化是很多降噪算法的核心步骤

软阈值化，是很多信号降噪算法的核心步骤，将绝对值小于某个阈值的特征删除掉，将绝对值大于这个阈值的特征朝着零的方向进行收缩。它可以通过以下公式来实现：

软阈值化的输出对于输入的导数为

由上可知，软阈值化的导数要么是1，要么是0。这个性质是和ReLU激活函数是相同的。因此，软阈值化也能够减小深度学习算法遭遇梯度弥散和梯度爆炸的风险。

在软阈值化函数中，阈值的设置必须符合两个的条件： 第一，阈值是正数；第二，阈值不能大于输入信号的最大值，否则输出会全部为零。

同时，阈值最好还能符合第三个条件：每个样本应该根据自身的噪声含量，有着自己独立的阈值。

这是因为，很多样本的噪声含量经常是不同的。例如经常会有这种情况，在同一个样本集里面，样本A所含噪声较少，样本B所含噪声较多。那么，如果是在降噪算法里进行软阈值化的时候，样本A就应该采用较大的阈值，样本B就应该采用较小的阈值。在深度神经网络中，虽然这些特征和阈值失去了明确的物理意义，但是基本的道理还是相通的。也就是说，每个样本应该根据自身的噪声含量，有着自己独立的阈值。

3.注意力机制

注意力机制在计算机视觉领域是比较容易理解的。动物的视觉系统可以快速扫描全部区域，发现目标物体，进而将注意力集中在目标物体上，以提取更多的细节，同时抑制无关信息。具体请参照注意力机制方面的文章。

Squeeze-and-Excitation Network（SENet）是一种较新的注意力机制下的深度学习方法。 在不同的样本中，不同的特征通道，在分类任务中的贡献大小，往往是不同的。SENet采用一个小型的子网络，获得一组权重，进而将这组权重与各个通道的特征分别相乘，以调整各个通道特征的大小。这个过程，就可以认为是在施加不同大小的注意力在各个特征通道上。

在这种方式下，每一个样本，都会有自己独立的一组权重。换言之，任意的两个样本，它们的权重，都是不一样的。在SENet中，获得权重的具体路径是，“全局池化→全连接层→ReLU函数→全连接层→Sigmoid函数”。

4.深度注意力机制下的软阈值化

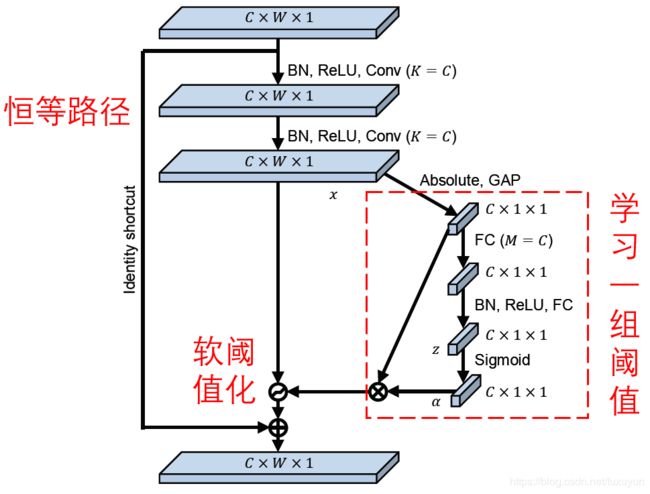
深度残差收缩网络借鉴了上述SENet的子网络结构，以实现注意力机制下的软阈值化。通过蓝色框内的子网络，就可以学习得到一组阈值，对各个特征通道进行软阈值化。

在这个子网络中，首先对输入特征图的所有特征，求它们的绝对值。然后经过全局均值池化和平均，获得一个特征，记为A。在另一条路径中，全局均值池化之后的特征图，被输入到一个小型的全连接网络。这个全连接网络以Sigmoid函数作为最后一层，将输出归一化到0和1之间，获得一个系数，记为α。最终的阈值可以表示为α×A。因此，阈值就是，一个0和1之间的数字×特征图的绝对值的平均。通过这种方式，保证了阈值为正，而且不会太大。

而且，不同的样本就有了不同的阈值。因此，在一定程度上，可以理解成一种特殊的注意力机制：注意到与当前任务无关的特征，通过软阈值化，将它们置为零；或者说，注意到与当前任务有关的特征，将它们保留下来。

5.深度残差收缩网络或许有更广泛的通用性

深度残差收缩网络事实上是一种通用的特征学习方法。这是因为很多特征学习的任务中，样本中或多或少都会包含一些噪声，以及不相关的信息。这些噪声和不相关的信息，有可能会对特征学习的效果造成影响。例如说：

在图片分类的时候，如果图片同时包含着很多其他的物体，那么这些物体就可以被理解成“噪声”；深度残差收缩网络或许能够借助注意力机制，注意到这些“噪声”，然后借助软阈值化，将这些“噪声”所对应的特征置为零，就有可能提高图像分类的准确率。

在语音识别的时候，如果在声音较为嘈杂的环境里，比如在马路边、工厂车间里聊天的时候，深度残差收缩网络也许可以提高语音识别的准确率，或者给出了一种能够提高语音识别准确率的思路。

6.基于深度残差收缩网络的MNIST图像分类程序

虽然深度残差收缩网络原先是应用在基于振动信号的机械故障诊断，但是深度残差收缩网络事实上是一种通用的特征学习方法，相信在很多任务（计算机视觉、语音、文本）中都可能有一定的用处。

下面是基于深度残差收缩网络的MNIST手写数字识别程序（程序很简单，仅供参考）：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Sat Dec 28 23:24:05 2019

Implemented using TensorFlow 1.0.1 and Keras 2.2.1
 
M. Zhao, S. Zhong, X. Fu, et al., Deep Residual Shrinkage Networks for Fault Diagnosis, 
IEEE Transactions on Industrial Informatics, 2019, DOI: 10.1109/TII.2019.2943898

@author: me
"""

from __future__ import print_function
import keras
import numpy as np
from keras.datasets import mnist
from keras.layers import Dense, Conv2D, BatchNormalization, Activation
from keras.layers import AveragePooling2D, Input, GlobalAveragePooling2D
from keras.optimizers import Adam
from keras.regularizers import l2
from keras import backend as K
from keras.models import Model
from keras.layers.core import Lambda
K.set_learning_phase(1)

# Input image dimensions
img_rows, img_cols = 28, 28

# The data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()

if K.image_data_format() == 'channels_first':
    x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
    x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
    input_shape = (1, img_rows, img_cols)
else:
    x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
    x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
    input_shape = (img_rows, img_cols, 1)

# Noised data
x_train = x_train.astype('float32') / 255. + 0.5*np.random.random([x_train.shape[0], img_rows, img_cols, 1])
x_test = x_test.astype('float32') / 255. + 0.5*np.random.random([x_test.shape[0], img_rows, img_cols, 1])
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')

# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)


def abs_backend(inputs):
    return K.abs(inputs)

def expand_dim_backend(inputs):
    return K.expand_dims(K.expand_dims(inputs,1),1)

def sign_backend(inputs):
    return K.sign(inputs)

def pad_backend(inputs, in_channels, out_channels):
    pad_dim = (out_channels - in_channels)//2
    return K.spatial_3d_padding(inputs, padding = ((0,0),(0,0),(pad_dim,pad_dim)))

# Residual Shrinakge Block
def residual_shrinkage_block(incoming, nb_blocks, out_channels, downsample=False,
                             downsample_strides=2):
    
    residual = incoming
    in_channels = incoming.get_shape().as_list()[-1]
    
    for i in range(nb_blocks):
        
        identity = residual
        
        if not downsample:
            downsample_strides = 1
        
        residual = BatchNormalization()(residual)
        residual = Activation('relu')(residual)
        residual = Conv2D(out_channels, 3, strides=(downsample_strides, downsample_strides), 
                          padding='same', kernel_initializer='he_normal', 
                          kernel_regularizer=l2(1e-4))(residual)
        
        residual = BatchNormalization()(residual)
        residual = Activation('relu')(residual)
        residual = Conv2D(out_channels, 3, padding='same', kernel_initializer='he_normal', 
                          kernel_regularizer=l2(1e-4))(residual)
        
        # Calculate global means
        residual_abs = Lambda(abs_backend)(residual)
        abs_mean = GlobalAveragePooling2D()(residual_abs)
        
        # Calculate scaling coefficients
        scales = Dense(out_channels, activation=None, kernel_initializer='he_normal', 
                       kernel_regularizer=l2(1e-4))(abs_mean)
        scales = BatchNormalization()(scales)
        scales = Activation('relu')(scales)
        scales = Dense(out_channels, activation='sigmoid', kernel_regularizer=l2(1e-4))(scales)
        scales = Lambda(expand_dim_backend)(scales)
        
        # Calculate thresholds
        thres = keras.layers.multiply([abs_mean, scales])
        
        # Soft thresholding
        sub = keras.layers.subtract([residual_abs, thres])
        zeros = keras.layers.subtract([sub, sub])
        n_sub = keras.layers.maximum([sub, zeros])
        residual = keras.layers.multiply([Lambda(sign_backend)(residual), n_sub])
        
        # Downsampling (it is important to use the pooL-size of (1, 1))
        if downsample_strides > 1:
            identity = AveragePooling2D(pool_size=(1,1), strides=(2,2))(identity)
            
        # Zero_padding to match channels (it is important to use zero padding rather than 1by1 convolution)
        if in_channels != out_channels:
            identity = Lambda(pad_backend)(identity, in_channels, out_channels)
        
        residual = keras.layers.add([residual, identity])
    
    return residual


# define and train a model
inputs = Input(shape=input_shape)
net = Conv2D(8, 3, padding='same', kernel_initializer='he_normal', kernel_regularizer=l2(1e-4))(inputs)
net = residual_shrinkage_block(net, 1, 8, downsample=True)
net = BatchNormalization()(net)
net = Activation('relu')(net)
net = GlobalAveragePooling2D()(net)
outputs = Dense(10, activation='softmax', kernel_initializer='he_normal', kernel_regularizer=l2(1e-4))(net)
model = Model(inputs=inputs, outputs=outputs)
model.compile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy'])
model.fit(x_train, y_train, batch_size=100, epochs=5, verbose=1, validation_data=(x_test, y_test))

# get results
K.set_learning_phase(0)
DRSN_train_score = model.evaluate(x_train, y_train, batch_size=100, verbose=0)
print('Train loss:', DRSN_train_score[0])
print('Train accuracy:', DRSN_train_score[1])
DRSN_test_score = model.evaluate(x_test, y_test, batch_size=100, verbose=0)
print('Test loss:', DRSN_test_score[0])
print('Test accuracy:', DRSN_test_score[1])

备注：

（1）深度残差收缩网络的结构比普通的深度残差网络复杂，也许更难训练。

（2）程序里只设置了一个基本模块，在更复杂的数据集上，可适当增加。

（3）如果遇到这个TypeError：softmax() got an unexpected keyword argument 'axis'，就点开tensorflow_backend.py，将return tf.nn.softmax(x, axis=axis)中的第一个axis改成dim即可。

 

参考网址

深度残差收缩网络：（四）注意力机制下的阈值设置

https://www.cnblogs.com/yc-9527/p/11604082.html

【深度残差收缩网络论文翻译】 Deep Residual Shrinkage Networks for Fault Diagnosis

https://www.jianshu.com/p/bcdc9d75a302

秒懂深度残差收缩网络

https://www.jianshu.com/p/90f1ef1b06bc

论文网址

M. Zhao, S. Zhong, X. Fu, et al., Deep residual shrinkage networks for fault diagnosis, IEEE Transactions on Industrial Informatics, DOI: 10.1109/TII.2019.2943898

https://ieeexplore.ieee.org/document/8850096