信息论入门：信息守恒定律与纠错码

Hamming编码研究

异或⊕的本质

其实“异或”这个名词的名字取得不好，叫“奇运算”都好听些。

以前我们学到异或和同或的时候讲到，异或指2个bit相异时值为1，同或指2个bit相同时值为1，于是我认为异或的逻辑意义就是2个bit值是否相同。但是后来发现异或运算（同或===异或+非）满足交换律和结合律，也就是说3个及以上的bit之间也可以毫无顺序的作异或运算。那么问题来了，3个bit之间怎么好说“相同”还是“相异”呢？

最后我在Photoshop里面2个图块间的”异或运算“功能上找到了线索，首先，PS中2个图块做异或操作如下，比如2个红色圆形之间异或：

其中最外层的黑色粗边框代表“全部”，当3个红圆之间异或的时候变成这丫：

发现了吗！在维恩图中，当我们用一个新的圈来异或已有的圈，我们相当于是在做『反色』操作。所以，异或操作是交换且结合的，因为谁管你哪个圈圈在上、哪个圈圈在下呢！

图中，每一个像素都是一个bit，bit的值是垂直于图片的所有图层的颜色（红色代表1，透明代表0）的异或值。

这让我想到奇偶校验，异或的本质就是所有参与运算的bit中，”1“的个数的奇偶性，或者是否是奇数。

异或和同或的本质就是奇偶校验。

 

信息守恒定律

霍金他老人家认为信息是虚拟化的物质，爱因斯坦认为物质即能量，所以，信息即能量，既然有能量守恒定律，也就有信息守恒定律（真的有）。

纠错码，是在传输过程中发生错误后能在收端自行发现或纠正的码，通常和原文一起发送给对端。假如纠错码是r位，那么从信息论的角度，数据中多出来了r位的信息，根据组合数公式（图），可以表示2^r种状态。

数学证明没有绝对的安全

多出来的2^r种状态能表示多少种错误情况呢？假如原文有k位，那么从0位错误到k+r位错误，根据上面的组合数公式，总共有2^(k+r)种出错情况，也就是要保证2^r>=2^(k+r)，即k==0，也就是没有原文，这种情况也不需要传输，也无需ISP在传输途中hack你的数据，对端也知道数据是啥了，比如你们约定统统传输11111111。。。

所以，没有绝对的安全。

 

可以纠错的摘要？

通常摘要算法是不可逆的，也没有纠错功能，海明码就是这样一个可以适度纠错的摘要算法。

上次介绍了《最短的摘要算法》——奇偶校验编码，产生1bit的摘要值，可以查奇数个bit的错误。

海明码（Hamming code）是一种纠错码，因为没有绝对的安全，海明码选择去纠正只有1bit出错的情况。也是在k位原文种添加r位校验位，因为校验码本身也会出错，总出错情况是k+r+1种，根据信息守恒定律，r需要满足2^r>=k+r+1，这个关于r不等式显然是有解的，这也是海明码的理论基础。

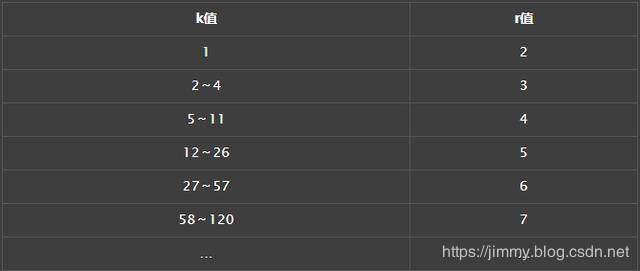
不等式的前几个通解如图所示：

 

虚拟比特？？

举个例子，k=4，r=3时的海明码如表所示：

首先，有3个校验位，但不能直接利用他们的排列组合来表示错误情况，因为校验位和原文是平等的，所以需要利用这3个校验位生成3个虚拟比特：G1，G2，G3。

物理bit	1	2	3	4	5	6	7	指误字	无错误	出错位
含义	p1	p2	B1	p3	B2	B3	B4			1	2	3	4	5	6	7
第三组				*	*	*	*	G3	0	0	0	0	1	1	1	1
第二组		*	*			*	*	G2	0	0	1	1	0	0	1	1
第一组	*		*		*		*	G1	0	1	0	1	0	1	0	1

 

根据虚拟化的思想，一个虚拟bit应该来自多个物理bit。这让我想到了对7位物理bit分组做摘要，由于摘要值仍然是一个bit，所以毫无疑问使用奇偶校验（异或）。

为了描述错误，任意一个物理bit发生错误（01对调），都会出现一个唯一的指误字G1G2G3，这个指误字是一个3位的字节，又因为k=4，r=3时，2^3 = 3+4+1，所以指误字的所有组合都会出现，接下来就是以“从0开始遍历二进制数”的方式开始为每一个物理比特分组，如表中的*号，指误字为000留给正确的情况，所以每组均采用偶校验。

为了使每一份组中都有且只有1个校验位，校验位放在2的自然数次幂的位置上，即1，2，4，8。。。

按照这个规律进行分组，每次编码时，校验位保证本组异或值为0，校验时也按照这个规则检验，最终指误字如果不为000，指误字的数值意义则代表了出错的位置。

应用场景

如果按照上面的例子，即（7,4）海明码来编码，则每4个bit就需要3bit校验位，数据量翻了0.75倍，显然是不合适的。因此k值要增大，很显然k越大r/k就越小，成本就越低，但是k不能无限增大，因为海明码只能检测1位错误，只适合1位出错的概率远远大于多位出错的概率，当原始数据量达到一定程度时，只有1位出错的可能性就非常小了，远远小于多位出错的可能性，这时候海明码就只能误判，从而失去了校验的意义。（误判的情况通常最终会在应用层发现错误，然后重传。。）

所以，海明码通常将数据位都保持在11位，校验位是4位，这样一个不多不少的吃水高度。