吴恩达机器学习逻辑回归python实现[对应ex2-ex2data1.txt数据集]
研一学生,初学机器学习,重心放在应用,弱化公式推导,能力有限,文中难免会有错误,恳请指正!QQ:245770710
此文是对网易云课堂上吴恩达老师的机器学习课程逻辑回归一章对应的课后作业的python实现。
1. 先对数据集进行观察,使用matplotlib将数据集绘制出散点图。
拿到一份数据想从中分析出一些内容,首先要了解拿到的数据,因此我们先把数据以散点图的形式绘制出来,观察其中的规律以确定用什么模型进行预测。
# 导入Matploylib库
from matplotlib import pyplot as plt
import matplotlib.ticker as ticker
# 导入训练数据
train_data = open("data/ex2data1.txt")
# 获取数据集的行数
lines = train_data.readlines()
# 定义x y数据 x1 y1:未通过 x2 y2:通过
x1 = []
y1 = []
x2 = []
y2 = []
# 循环处理所有的数据
for line in lines:
scores = line.split(",")
isQualified = scores[2].replace("\n", "")
if isQualified == "0":
x1.append(float(scores[0]))
y1.append(float(scores[1]))
else:
x2.append(float(scores[0]))
y2.append(float(scores[1]))
# 画图
plt.xlabel("Exam 1 score")
plt.ylabel("Exam 2 score")
# 记号形状 颜色 点的大小 设置标签
plt.scatter(x1, y1, marker='o', color='red', s=15, label='Not admitted')
plt.scatter(x2, y2, marker='x', color='green', s=15, label='Admitted')
# 注释的显示位置:右上角
plt.legend(loc='upper right')
# 设置坐标轴上刻度的精度
plt.gca().xaxis.set_major_formatter(ticker.FormatStrFormatter('%.1f'))
plt.gca().yaxis.set_major_formatter(ticker.FormatStrFormatter('%.1f'))
plt.show()
数据集散点图
2.观察测试数据集的图像,定义预测函数h(x)
观察图像可得,对测试数据集进行分类只需一条直线即可,因为有两个输入参数(即第一次的分数x1和第二次的分数2),所以设
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 = θ T X h_θ(x) = θ_0+θ_1x_1+θ_2x_2=θ_0x_0+θ_1x_1+θ_2x_2=θ^TX hθ(x)=θ0+θ1x1+θ2x2=θ0x0+θ1x1+θ2x2=θTX
其中x0均为1,此处需要注意的是,在代码中实现时我们的特征矩阵是n+1个,多出来的一个特征就是x0,并且x0都为1,之所以添加一个x0的原因是在代码中进行计算时是以矩阵的形式进行的,因此θ矩阵转置后的行数必须与特征矩阵X的列数一致,如果这两个数不一致则无法进行矩阵运算。
因此 sigmoid 函数为
g ( z ) = g ( h θ ( x ) ) = 1 1 + e − h θ ( x ) g(z) = g( hθ(x) ) = \frac{1}{1+e^{-h_θ(x)}} g(z)=g(hθ(x))=1+e−hθ(x)1
python 代码定义h(x)函数:
# 定义h(x)预测函数:theta为转置后的矩阵,即theta是一个n行1列的矩阵
def hypothesis(theta, x):
return np.dot(x, theta)
python代码定义sigmoid函数:
# 定义sigmoid函数
def sigmoid(theta, x):
z = hypothesis(theta, x)
return 1.0 / (1 + exp(-z))
3.定义代价函数
根据Andrew Ng的视频,逻辑回归的代价函数如下;
J ( θ ) = 1 M ∑ i = 1 m [ − y ( i ) l o g ( θ 0 + θ 1 x 1 i + θ 2 x 2 i ) − ( 1 − y ( i ) ) l o g ( 1 − θ 0 − θ 1 x 1 i − θ 2 x 2 i ) ] J(θ)=\frac{1}{M} \sum_{i=1}^{m}[-y^{(i)}log(θ_0+θ_1x_1^i+θ_2x_2^i)-(1-y^{(i)})log(1-θ_0-θ_1x_1^i-θ_2x_2^i)] J(θ)=M1i=1∑m[−y(i)log(θ0+θ1x1i+θ2x2i)−(1−y(i))log(1−θ0−θ1x1i−θ2x2i)]
此处需要注意的是我们在python代码中实现时采用的矩阵运算(当然也可以使用for循环代替矩阵),因此需要对代价函数进行向量化。使用矩阵运算的速度远高于for循环,具体的对比见https://www.cnblogs.com/liaohuiqiang/p/7663616.html,本文不再赘述。从代价函数到向量化的过程请参考https://blog.csdn.net/quiet_girl/article/details/70098009?locationNum=5&fps=1,在这篇文章中讲的线性回归的向量化过程,逻辑回归代价函数的向量化请参照此篇文章自行理解,此处直接给出该代价函数的向量化后的结果,如下所示。
根据向量化后的代价函数定义python代码:
# 定义代价函数
def cost(theta, X, y):
return np.mean(-y * np.log(sigmoid(theta, X)) - (1 - y) * np.log(1 - sigmoid(theta, X)))
在代价函数这一部分,需要注意的是:代价函数的定义方式决定了下一步是采用梯度下降算法还是梯度上升算法,梯度上升和梯度下降都是求预测值和真实值最接近时theta的值,不同的是梯度上升用于求最大值,梯度下降用于求最小值,具体介绍请参考https://blog.csdn.net/xiaoxiangzi222/article/details/55097570。
而Andrew Ng 在视频直接给出了代价函数J(θ),但是没有给出具体的过程。实际上在此处代价函数可以有两种形式,一种是Andrew Ng给出的代价函数,也就是上文中给出的J(θ),另外一种是在J(θ)的基础上添加一个符号即“-J(θ)”,添加一个负号以后,图像的开口方向就会变反,因此这两个代价函数一个采用梯度下降另外一个采用梯度上升。由于Andrew Ng在前面的视频中先讲解了梯度下降法,因此在逻辑回归部分他继续沿用梯度下降,因此他将代价函数定义为
J ( θ ) = 1 M ∑ i = 1 m [ − y ( i ) l o g ( θ 0 + θ 1 x 1 i + θ 2 x 2 i ) − ( 1 − y ( i ) ) l o g ( 1 − θ 0 − θ 1 x 1 i − θ 2 x 2 i ) ] J(θ)=\frac{1}{M} \sum_{i=1}^{m}[-y^{(i)}log(θ_0+θ_1x_1^i+θ_2x_2^i)-(1-y^{(i)})log(1-θ_0-θ_1x_1^i-θ_2x_2^i)] J(θ)=M1i=1∑m[−y(i)log(θ0+θ1x1i+θ2x2i)−(1−y(i))log(1−θ0−θ1x1i−θ2x2i)]
此处我们沿用Andrew Ng定义的代价函数。
4.对应的梯度下降函数
采用批量梯度下降,对应的向量化为:
![]()
对应的python代码为:
# 梯度下降函数
def gradient(theta, X, y):
return (1 / len(X)) * X.T @ (sigmoid(theta, X) - y)
5.求解最优解
因3中定义的代价函数如下,带有负号,因此需要采用梯度下降法求解。
J ( θ ) = 1 M ∑ i = 1 m [ − y ( i ) l o g ( θ 0 + θ 1 x 1 i + θ 2 x 2 i ) − ( 1 − y ( i ) ) l o g ( 1 − θ 0 − θ 1 x 1 i − θ 2 x 2 i ) ] J(θ)=\frac{1}{M} \sum_{i=1}^{m}[-y^{(i)}log(θ_0+θ_1x_1^i+θ_2x_2^i)-(1-y^{(i)})log(1-θ_0-θ_1x_1^i-θ_2x_2^i)] J(θ)=M1i=1∑m[−y(i)log(θ0+θ1x1i+θ2x2i)−(1−y(i))log(1−θ0−θ1x1i−θ2x2i)]
若代价函数为
J ( θ ) = − 1 M ∑ i = 1 m [ − y ( i ) l o g ( θ 0 + θ 1 x 1 i + θ 2 x 2 i ) − ( 1 − y ( i ) ) l o g ( 1 − θ 0 − θ 1 x 1 i − θ 2 x 2 i ) ] J(θ)=-\frac{1}{M} \sum_{i=1}^{m}[-y^{(i)}log(θ_0+θ_1x_1^i+θ_2x_2^i)-(1-y^{(i)})log(1-θ_0-θ_1x_1^i-θ_2x_2^i)] J(θ)=−M1i=1∑m[−y(i)log(θ0+θ1x1i+θ2x2i)−(1−y(i))log(1−θ0−θ1x1i−θ2x2i)]
则用梯度上升算法求解。梯度上升的实现方式请参照《机器学习实战》一书中的Logistic回归一章。此文使用第一种代价函数(Andrew Ng视频中用的那个),采用梯度下降的方式求解。
此处我直接使用 scipy.optimize.minimize() 方法求解代价函数的最优解。
代码如下:
import scipy.optimize as opt
result = opt.minimize(fun=cost, x0=theta, args=(X, y), method='Newton-CG', jac=gradient)
其中cost为代价函数,theta为初始值,一般设置为0,args传入的X,y分别是训练数据的特征和标志位,method是指定优化算法。返回的result中x就是最终求得的theta值。result中的属性如下图所示:
x中的第一个值(-25.14212556)对应的是theta0, 第2个值(0.20607808)对应的是theta1, 第三个值对应的theta3。
6. 根据求得的theta值画出预测函数的图像
画出预测函数的图像比用验证数据进行验证的效果更佳明显,因此在第1步画出的散点图的基础上,把预测函数的图像再画出来。
在第5步中我们以及求得了三个theta的值,而我们的预测函数为
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 h_θ(x) = θ_0+θ_1x_1+θ_2x_2 hθ(x)=θ0+θ1x1+θ2x2
因此我们设x1取[30, 40, 50, … ,100],根据theta的取值求出x2的值,之后根据x1, x2的值画出预测函数对应的图像。python代码如下:
# 设置训练得到的模型对应的直线,即h(x)对应的直线
# 设置x的取值范围:[30, 110]步长为10
x = np.arange(30, 110, 10)
y = (-result.x[0] - result.x[1] * x) / result.x[2]
plt.plot(x, y)
最终的效果如下图所示:
7.完整代码
数据集为吴恩达机器学习逻辑回归作业ex2中的ex2data1.txt。代码使用时注意修改代码中数据集文件的路径。
# 导入Matploylib库
from matplotlib import pyplot as plt
from numpy import *
import matplotlib.ticker as ticker
import numpy as np
import scipy.optimize as opt
# 定义h(x)预测函数:theat为转置后的矩阵
def hypothesis(theta, x):
return np.dot(x, theta)
# 定义sigmoid函数
def sigmoid(theta, x):
z = hypothesis(theta, x)
return 1.0 / (1 + exp(-z))
# 定义代价函数
def cost(theta, X, y):
return np.mean(-y * np.log(sigmoid(theta, X)) - (1 - y) * np.log(1 - sigmoid(theta, X)))
# 梯度下降函数
def gradient(theta, X, y):
return (1 / len(X)) * X.T @ (sigmoid(theta, X) - y)
'''
绘图:绘制训练数据的散点图和h(x)预测函数对应的直线
'''
def draw():
# 定义x y数据 x1 y1:未通过 x2 y2:通过
x1 = []
y1 = []
x2 = []
y2 = []
# 导入训练数据
train_data = open("data/ex2data1.txt")
lines = train_data.readlines()
for line in lines:
scores = line.split(",")
# 去除标记后面的换行符
isQualified = scores[2].replace("\n", "")
# 根据标记将两次成绩放到对应的数组
if isQualified == "0":
x1.append(float(scores[0]))
y1.append(float(scores[1]))
else:
x2.append(float(scores[0]))
y2.append(float(scores[1]))
# 设置标题和横纵坐标的标注
plt.xlabel("Exam 1 score")
plt.ylabel("Exam 2 score")
# 设置通过测试和不通过测试数据的样式。其中x y为两次的成绩,marker:记号形状 color:颜色 s:点的大小 label:标注
plt.scatter(x1, y1, marker='o', color='red', s=15, label='Not admitted')
plt.scatter(x2, y2, marker='x', color='green', s=15, label='Admitted')
# 标注[即上两行中的label]的显示位置:右上角
plt.legend(loc='upper right')
# 设置坐标轴上刻度的精度为一位小数。因训练数据中的分数的小数点太多,若不限制坐标轴上刻度显示的精度,影响最终散点图的美观度
plt.gca().xaxis.set_major_formatter(ticker.FormatStrFormatter('%.1f'))
plt.gca().yaxis.set_major_formatter(ticker.FormatStrFormatter('%.1f'))
# 设置训练得到的模型对应的直线,即h(x)对应的直线
# 设置x的取值范围:[30, 110]步长为10
x = np.arange(30, 110, 10)
y = (-result.x[0] - result.x[1] * x) / result.x[2]
plt.plot(x, y)
# 显示
plt.show()
'''
数据预先处理:将两次成绩与是否通过测试的标记分别生成矩阵,并将标记的矩阵转置。
'''
def init_data():
# 两次成绩对应的特征矩阵
data = []
# 标记对应的矩阵
label = []
# 读取文件
train_data = open("data/ex2data1.txt")
lines = train_data.readlines()
for line in lines:
scores = line.split(",")
# 去除标记后面的换行符
isQualified = scores[2].replace("\n", "")
# 添加特征x0,设置为1
data.append([1, float(scores[0]), float(scores[1])])
label.append(int(isQualified))
# 标记矩阵转置,返回特征矩阵和标记矩阵
return np.array(data), np.array(label).transpose()
'''
主函数
'''
if __name__ == '__main__':
# 初始化数据
X, y = init_data()
# 初始化theta:三行一列的0矩阵
theta = np.zeros((3, 1))
# 使用minimize函数求解
result = opt.minimize(fun=cost, x0=theta, args=(X, y), method='Newton-CG', jac=gradient)
print(result)
# 绘图
draw()
8.参考文献
[1] https://www.cnblogs.com/liaohuiqiang/p/7663616.html
[2] https://blog.csdn.net/quiet_girl/article/details/70098009?locationNum=5&fps=1
[3] https://blog.csdn.net/xiaoxiangzi222/article/details/55097570
[4] 《机器学习实战》——【美】Peter Harington
[5] https://github.com/HuangCongQing/MachineLearning_Ng
![吴恩达机器学习逻辑回归python实现[对应ex2-ex2data1.txt数据集]_第1张图片](http://img.e-com-net.com/image/info8/6a1b4c2f21fc485681280520a91c9622.jpg)
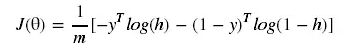
![吴恩达机器学习逻辑回归python实现[对应ex2-ex2data1.txt数据集]_第2张图片](http://img.e-com-net.com/image/info8/4cecb3c1b7bf49d7a76c7b05de0ef29d.jpg)
![吴恩达机器学习逻辑回归python实现[对应ex2-ex2data1.txt数据集]_第3张图片](http://img.e-com-net.com/image/info8/439ec78810ba4fac909735a1366c7086.jpg)