吴恩达Coursera深度学习课程 deeplearning.ai (4-1) 卷积神经网络--编程作业

Part 1：卷积神经网络

本周课程将利用numpy实现卷积层(CONV) 和 池化层(POOL), 包含前向传播和可选的反向传播。

变量说明

• 上标 [l] [ l ] 表示神经网络的第几层
• 上标 (i) ( i ) 表示第几个样本
• 上标 [i] [ i ] 表示第几个mini-batch
• 下标 i i 表示向量的第几个维度
• nH n H , nW n W , nC n C 分别代表图片的高，宽和通道数
• nHprev n H p r e v , nWprev n W p r e v , nCprev n C p r e v 分别代表上一层图片的高，宽和通道数

1 导包

import numpy as np # 科学计算的
import h5py # 读取数据文件的
import matplotlib.pyplot as plt # 画图的

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1) # 使随机函数一致的

2 作业大纲

• 卷积层
  
  • Zero Padding
  • Convolve window
  • Convolution forward
  • Convolution backward (optional)
• 池化层
  
  • Pooling forward
  • Create mask
  • Distribute value
  • Pooling backward (optional)

本次作业我们采用numpy方式实现（需要实现反向传播），之后的作业可以采用tensorflow实现

3 卷积层

实现如下卷几层：将输入转化为不同size的输出。

3.1 Zero-Padding (填充0作为Padding)

Padding 的好处

• 不加Padding时每次卷积图片都会缩小，加上Padding后图片可以自由设置大小，比如保持不变的SAME模式
• 保留图片边缘的信息，如果没有Padding，边缘信息作用的输出非常少，会再一定程度上丢失信息

练习

用0位图片填充Padding，以下代码可以为(5,5,5,5,5)的数组a添加Padding：为第2维添加 pad =1，为第4维添加 pad=3，其余维度pad=0

a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), 'constant', constant_values = (..,..))

代码

# GRADED FUNCTION: zero_pad

def zero_pad(X, pad):
    """
    Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, 
    as illustrated in Figure 1.

    Argument:
    X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images
    pad -- integer, amount of padding around each image on vertical and horizontal dimensions

    Returns:
    X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C)
    """

    ### START CODE HERE ### (≈ 1 line)
    X_pad = np.pad(X, ((0,0), (pad,pad), (pad,pad), (0,0)), 'constant')
    ### END CODE HERE ###

    return X_pad

##########################################

np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_pad = zero_pad(x, 2)
print ("x.shape =", x.shape)
print ("x_pad.shape =", x_pad.shape)
print ("x[1,1] =", x[1,1])
print ("x_pad[1,1] =", x_pad[1,1])

fig, axarr = plt.subplots(1, 2)
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0,:,:,0])

# x.shape = (4, 3, 3, 2)
# x_pad.shape = (4, 7, 7, 2)
# x[1,1] = [[ 0.90085595 -0.68372786]
#  [-0.12289023 -0.93576943]
#  [-0.26788808  0.53035547]]
# x_pad[1,1] = [[ 0.  0.]
#  [ 0.  0.]
#  [ 0.  0.]
#  [ 0.  0.]
#  [ 0.  0.]
#  [ 0.  0.]
#  [ 0.  0.]]
# 
# 

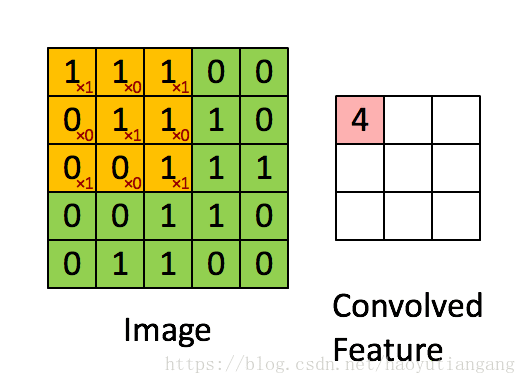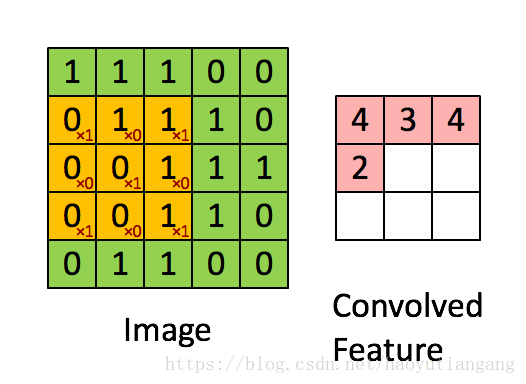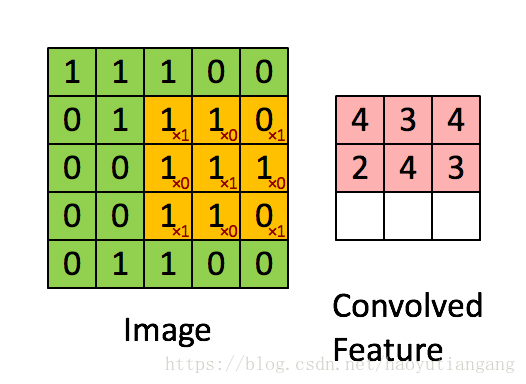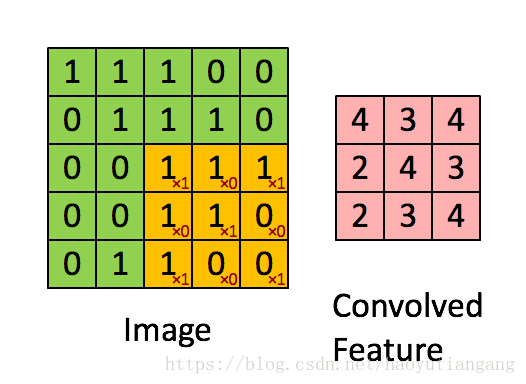
3.2 单步卷积层

利用卷积核(filter)遍历输入(input)得到输出(output)

• 卷积核的计算：每次对应元素相乘再加和作为输出的一个元素，相当于WX
• 真正的输出：A = sigmoid(WX+b)也就是在卷积的基础上加上偏移量再进行sigmoid非线性运算

# GRADED FUNCTION: conv_single_step

def conv_single_step(a_slice_prev, W, b):
    """
    Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation 
    of the previous layer.

    Arguments:
    a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
    W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
    b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)

    Returns:
    Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data
    """

    ### START CODE HERE ### (≈ 2 lines of code)
    # Element-wise product between a_slice and W. Do not add the bias yet.
    s = a_slice_prev * W
    # Sum over all entries of the volume s.
    Z = np.sum(s)
    # Add bias b to Z. Cast b to a float() so that Z results in a scalar value.
    Z = Z + b
    ### END CODE HERE ###

    return Z

########################################

np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)

Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)

# Z = [[[-6.99908945]]]

3.3 卷积神经网络-前向传播

运用多个卷积核(filter)处理输出图像，每个卷积核输出一个2维图像，多个卷积核输出多个2维图像作为通道叠加在一起。

提示

1. 选取图像分片

a_slice_prev = a_prev[0:2,0:2,:]

1. 选取分片之前，应该先定义分片的范围（vert_start, vert_end, horiz_start, horiz_end）
   

2. 输出图片的大小
   

   nHnWnC=⌊nHprev−f+2padstrid⌋+1=⌊nWprev−f+2padstrid⌋+1=numoffilters n H = ⌊ n H p r e v − f + 2 p a d s t r i d ⌋ + 1 n W = ⌊ n W p r e v − f + 2 p a d s t r i d ⌋ + 1 n C = n u m o f f i l t e r s

# GRADED FUNCTION: conv_forward

def conv_forward(A_prev, W, b, hparameters):
    """
    Implements the forward propagation for a convolution function

    Arguments:
    A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    W -- Weights, numpy array of shape (f, f, n_C_prev, n_C)
    b -- Biases, numpy array of shape (1, 1, 1, n_C)
    hparameters -- python dictionary containing "stride" and "pad"

    Returns:
    Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward() function
    """

    ### START CODE HERE ###
    # Retrieve dimensions from A_prev's shape (≈1 line)  
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape

    # Retrieve dimensions from W's shape (≈1 line)
    (f, f, n_C_prev, n_C) = W.shape

    # Retrieve information from "hparameters" (≈2 lines)
    stride = hparameters["stride"]
    pad = hparameters["pad"]

    # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines)
    n_H = int((n_H_prev - f + 2*pad) / stride + 1)
    n_W = int((n_W_prev - f + 2*pad) / stride + 1)

    # Initialize the output volume Z with zeros. (≈1 line)
    Z = np.zeros((m, n_H, n_W, n_C))

    # Create A_prev_pad by padding A_prev
    A_prev_pad = zero_pad(A_prev, pad)

    for i in range(m):                               # loop over the batch of training examples
        a_prev_pad = A_prev_pad[i, :, :, :]                               # Select ith training example's padded activation
        for h in range(n_H):                           # loop over vertical axis of the output volume
            for w in range(n_W):                       # loop over horizontal axis of the output volume
                for c in range(n_C):                   # loop over channels (= #filters) of the output volume

                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = stride * h
                    vert_end = vert_start + f
                    horiz_start = stride * w
                    horiz_end = horiz_start + f

                    # Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)
                    a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]

                    # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line)
                    Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:, :, :, c], b[:, :, :, c])

    ### END CODE HERE ###

    # Making sure your output shape is correct
    assert(Z.shape == (m, n_H, n_W, n_C))

    # Save information in "cache" for the backprop
    cache = (A_prev, W, b, hparameters)

    return Z, cache

#########################################################3

np.random.seed(1)
A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
               "stride": 2}

Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
print("Z's mean =", np.mean(Z))
print("Z[3,2,1] =", Z[3,2,1])
print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3])

# Z's mean = 0.0489952035289
# Z[3,2,1] = [-0.61490741 -6.7439236  -2.55153897  1.75698377  3.56208902  # 0.53036437
#   5.18531798  8.75898442]
# cache_conv[0][1][2][3] = [-0.20075807  0.18656139  0.41005165]

理论上，卷几层还需要一个激活函数

# Convolve the window to get back one output neuron
Z[i, h, w, c] = ...
# Apply activation
A[i, h, w, c] = activation(Z[i, h, w, c])

4 池化层

池化层将图片的宽/高进行压缩(通道数保持不变)，抽取局部像素的特征作为一个像素，也可以使算法对于图片的变化具有鲁棒性。

两种池化的方式

• 最大值池化：利用(f,f)的窗口对图片进行运算，窗口元素取最大值
• 平均值池化：利用(f,f)的窗口对图片进行运算，窗口元素取平均值

池化层拥有一个参数f, 表示池化窗口的大小(f,f)，但是没有需要反向传播时学习的参数。

4.1 池化层-前向传播

实现 MAX-POOL 和 AVG-POOL

提示

池化层的输出大小: 和卷积运算相比，每个通道单独运算，通道数不变)

nHnWnC=⌊nHprev−f+2padstrid⌋+1=⌊nWprev−f+2padstrid⌋+1=nCprev n H = ⌊ n H p r e v − f + 2 p a d s t r i d ⌋ + 1 n W = ⌊ n W p r e v − f + 2 p a d s t r i d ⌋ + 1 n C = n C p r e v

# GRADED FUNCTION: pool_forward

def pool_forward(A_prev, hparameters, mode = "max"):
    """
    Implements the forward pass of the pooling layer

    Arguments:
    A_prev -- Input data, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    hparameters -- python dictionary containing "f" and "stride"
    mode -- the pooling mode you would like to use, defined as a string ("max" or "average")

    Returns:
    A -- output of the pool layer, a numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters 
    """

    # Retrieve dimensions from the input shape
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape

    # Retrieve hyperparameters from "hparameters"
    f = hparameters["f"]
    stride = hparameters["stride"]

    # Define the dimensions of the output
    n_H = int(1 + (n_H_prev - f) / stride)
    n_W = int(1 + (n_W_prev - f) / stride)
    n_C = n_C_prev

    # Initialize output matrix A
    A = np.zeros((m, n_H, n_W, n_C))              

    ### START CODE HERE ###
    for i in range(m):                         # loop over the training examples
        for h in range(n_H):                     # loop on the vertical axis of the output volume
            for w in range(n_W):                 # loop on the horizontal axis of the output volume
                for c in range (n_C):            # loop over the channels of the output volume

                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = h * stride
                    vert_end = vert_start + f
                    horiz_start = w * stride
                    horiz_end = horiz_start + f

                    # Use the corners to define the current slice on the ith training example of A_prev, channel c. (≈1 line)
                    a_prev_slice = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c]

                    # Compute the pooling operation on the slice. Use an if statment to differentiate the modes. Use np.max/np.mean.
                    if mode == "max":
                        A[i, h, w, c] = np.max(a_prev_slice)
                    elif mode == "average":
                        A[i, h, w, c] = np.mean(a_prev_slice)

    ### END CODE HERE ###

    # Store the input and hparameters in "cache" for pool_backward()
    cache = (A_prev, hparameters)

    # Making sure your output shape is correct
    assert(A.shape == (m, n_H, n_W, n_C))

    return A, cache

###################################

np.random.seed(1)
A_prev = np.random.randn(2, 4, 4, 3)
hparameters = {"stride" : 2, "f": 3}

A, cache = pool_forward(A_prev, hparameters)
print("mode = max")
print("A =", A)
print()
A, cache = pool_forward(A_prev, hparameters, mode = "average")
print("mode = average")
print("A =", A)

# mode = max
# A = [[[[ 1.74481176  0.86540763  1.13376944]]]
# 
# 
#  [[[ 1.13162939  1.51981682  2.18557541]]]]
# 
# mode = average
# A = [[[[ 0.02105773 -0.20328806 -0.40389855]]]
# 
# 
#  [[[-0.22154621  0.51716526  0.48155844]]]]

恭喜你！完成了卷积神经网络的前向传播，下面反向传播的内容为可选部分。

5 卷积神经网络的反向传播(可选)

卷积神经网络的反向传播比较复杂，大部分框架也都提供了反向传播的功能，所以不做强制要求。

注意(在这里)：

• A 表示的是每个位置WX+b 加和之后 的值 (这里没有加入sigmoid的非线性部分)
• Z 表示输出图片某个位置(h,w)的WX+b的值
• dA 表示整体输出的A的梯度
• dZ 表示输出图片某位置Z的梯度

5.1 卷积层的反向传播

5.1.1 计算 dA

这是利用卷积核Wc和样本数据计算dA的公式

dA+=∑h=0nH∑w=0nWWc×dZhw d A + = ∑ h = 0 n H ∑ w = 0 n W W c × d Z h w

其中，Wc是卷积核(filter), dZ_hw是第Z层卷积在输出图片中(h,w)处输出代价函数的梯度常量。

每次都用同一个卷积核乘以不同位置的dZ，是因为前向传播时我们卷积核遍历输入图片得到了最后的Z，所以在反向传播计算dA时，我们需要将各个分片的梯度加起来。

da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]

5.1.2 计算 dW

这是计算dWc的公式，dWc是一个卷积核的梯度

dWc+=∑h=0nH∑w=0nWaslice×dZhw d W c + = ∑ h = 0 n H ∑ w = 0 n W a s l i c e × d Z h w

其中a_{slice}表示用于得到激活函数Zij的输入图片的切片，所以需要将每个切片产生的梯度都加起来才能得到dW

dW[:,:,:,c] += a_slice * dZ[i, h, w, c]

5.1.3 计算 db

以下是计算db的公式

db=∑h∑wdZhw d b = ∑ h ∑ w d Z h w

这里讲各个位置的dZ相加得到db

db[:,:,:,c] += dZ[i, h, w, c]

练习

实现conv_backward方法，需要将所有的训练样本，卷积核，宽，高都相加起来，然后利用上面的三个公式计算梯度。

def conv_backward(dZ, cache):
    """
    Implement the backward propagation for a convolution function

    Arguments:
    dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward(), output of conv_forward()

    Returns:
    dA_prev -- gradient of the cost with respect to the input of the conv layer (A_prev),
               numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    dW -- gradient of the cost with respect to the weights of the conv layer (W)
          numpy array of shape (f, f, n_C_prev, n_C)
    db -- gradient of the cost with respect to the biases of the conv layer (b)
          numpy array of shape (1, 1, 1, n_C)
    """

    ### START CODE HERE ###
    # Retrieve information from "cache"
    (A_prev, W, b, hparameters) = cache

    # Retrieve dimensions from A_prev's shape
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape

    # Retrieve dimensions from W's shape
    (f, f, n_C_prev, n_C) = W.shape

    # Retrieve information from "hparameters"
    stride = hparameters['stride']
    pad = hparameters['pad']

    # Retrieve dimensions from dZ's shape
    (m, n_H, n_W, n_C) = dZ.shape

    # Initialize dA_prev, dW, db with the correct shapes
    dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))
    dW = np.zeros((f, f, n_C_prev, n_C))
    db = np.zeros((1, 1, 1, n_C))

    # Pad A_prev and dA_prev
    A_prev_pad = zero_pad(A_prev, pad)
    dA_prev_pad = zero_pad(dA_prev, pad)

    for i in range(m):                       # loop over the training examples

        # select ith training example from A_prev_pad and dA_prev_pad
        a_prev_pad = A_prev_pad[i, :, :, :]
        da_prev_pad = dA_prev_pad[i, :, :, :]

        for h in range(n_H):                   # loop over vertical axis of the output volume
            for w in range(n_W):               # loop over horizontal axis of the output volume
                for c in range(n_C):           # loop over the channels of the output volume

                    # Find the corners of the current "slice"
                    vert_start = h * stride
                    vert_end = vert_start + f
                    horiz_start = w * stride
                    horiz_end = horiz_start + f

                    # Use the corners to define the slice from a_prev_pad
                    a_slice = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]

                    # Update gradients for the window and the filter's parameters using the code formulas given above
                    da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]
                    dW[:,:,:,c] += a_slice * dZ[i, h, w, c]
                    db[:,:,:,c] += dZ[i, h, w, c]

        # Set the ith training example's dA_prev to the unpaded da_prev_pad (Hint: use X[pad:-pad, pad:-pad, :])
        dA_prev[i, :, :, :] = da_prev_pad[pad:-pad, pad:-pad, :]
    ### END CODE HERE ###

    # Making sure your output shape is correct
    assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))

    return dA_prev, dW, db

########################################

np.random.seed(1)
dA, dW, db = conv_backward(Z, cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))

# dA_mean = 1.45243777754
# dW_mean = 1.72699145831
# db_mean = 7.83923256462

5.2 池化层-反向传播

池化层不需要学习任何参数，仅需要将反向传播中的梯度反向传递过去以备下游使用。

5.2.1 最大值池化-反向传播

首先我们需要实现一个面具窗口，盖住所有非Max的元素(0), 展示Max的元素(1)。

X=[1432]→M=[0100] X = [ 1 3 4 2 ] → M = [ 0 0 1 0 ]

练习

实现create_mask_from_window()

提示

• np.max() 求出矩阵最大值
• A = (X == x) 将会返回如下的A:

A[i,j] = True if X[i,j] = x
A[i,j] = False if X[i,j] != x

这里不考虑矩阵中有多个最大值的情况

def create_mask_from_window(x):
    """
    Creates a mask from an input matrix x, to identify the max entry of x.

    Arguments:
    x -- Array of shape (f, f)

    Returns:
    mask -- Array of the same shape as window, contains a True at the position corresponding to the max entry of x.
    """

    ### START CODE HERE ### (≈1 line)
    mask = (x == np.max(x))
    ### END CODE HERE ###

    return mask

#####################################3

np.random.seed(1)
x = np.random.randn(2,3)
mask = create_mask_from_window(x)
print('x = ', x)
print("mask = ", mask)

# x =  [[ 1.62434536 -0.61175641 -0.52817175]
#  [-1.07296862  0.86540763 -2.3015387 ]]
# mask =  [[ True False False]
#  [False False False]]

为什么要跟踪最大值在矩阵中的位置，因为最大值影响了输出，而反向传播时梯度影响的应该是最大值位置的输入，与其他位置的输入无关。

5.2.2 平均值池化-反向传播

与最大值池化不同，平均值池化中每个元素都以相同的权重作用到了输出上，所以平均值池化的面具矩阵应该是将dZ均衡分布的。例如(2,2)的矩阵面具为：

dZ=1→dZ=[1/41/41/41/4] d Z = 1 → d Z = [ 1 / 4 1 / 4 1 / 4 1 / 4 ]

提示

average = dz / (n_H * n_W)

练习

实现dZ的均衡分布

def distribute_value(dz, shape):
    """
    Distributes the input value in the matrix of dimension shape

    Arguments:
    dz -- input scalar
    shape -- the shape (n_H, n_W) of the output matrix for which we want to distribute the value of dz

    Returns:
    a -- Array of size (n_H, n_W) for which we distributed the value of dz
    """

    ### START CODE HERE ###
    # Retrieve dimensions from shape (≈1 line)
    (n_H, n_W) = shape

    # Compute the value to distribute on the matrix (≈1 line)
    average = dz / (n_H * n_W)

    # Create a matrix where every entry is the "average" value (≈1 line)
    a = average * np.ones(shape)
    ### END CODE HERE ###

    return a

#####################################

a = distribute_value(2, (2,2))
print('distributed value =', a)

# distributed value = [[ 0.5  0.5]
#  [ 0.5  0.5]]

5.2.3 集成：池化层-反向传播

实现具有max/average两种模式的池化层反向传播函数。

def pool_backward(dA, cache, mode = "max"):
    """
    Implements the backward pass of the pooling layer

    Arguments:
    dA -- gradient of cost with respect to the output of the pooling layer, same shape as A
    cache -- cache output from the forward pass of the pooling layer, contains the layer's input and hparameters 
    mode -- the pooling mode you would like to use, defined as a string ("max" or "average")

    Returns:
    dA_prev -- gradient of cost with respect to the input of the pooling layer, same shape as A_prev
    """

    ### START CODE HERE ###

    # Retrieve information from cache (≈1 line)
    (A_prev, hparameters) = cache

    # Retrieve hyperparameters from "hparameters" (≈2 lines)
    stride = hparameters['stride']
    f = hparameters['f']

    # Retrieve dimensions from A_prev's shape and dA's shape (≈2 lines)
    m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape
    m, n_H, n_W, n_C = dA.shape

    # Initialize dA_prev with zeros (≈1 line)
    dA_prev = np.zeros(np.shape(A_prev))

    for i in range(m):                       # loop over the training examples

        # select training example from A_prev (≈1 line)
        a_prev = A_prev[i, :, :, :]

        for h in range(n_H):                   # loop on the vertical axis
            for w in range(n_W):               # loop on the horizontal axis
                for c in range(n_C):           # loop over the channels (depth)

                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = h * stride
                    vert_end = vert_start + f
                    horiz_start = w * stride
                    horiz_end = horiz_start + f

                    # Compute the backward propagation in both modes.
                    if mode == "max":

                        # Use the corners and "c" to define the current slice from a_prev (≈1 line)
                        a_prev_slice = a_prev[vert_start:vert_end, horiz_start:horiz_end, c]
                        # Create the mask from a_prev_slice (≈1 line)
                        mask = create_mask_from_window(a_prev_slice)
                        # Set dA_prev to be dA_prev + (the mask multiplied by the correct entry of dA) (≈1 line)
                        dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += np.multiply(mask, dA[i, h, w, c])


                    elif mode == "average":

                        # Get the value a from dA (≈1 line)
                        da = dA[i, h, w, c]
                        # Define the shape of the filter as fxf (≈1 line)
                        shape = (f, f)
                        # Distribute it to get the correct slice of dA_prev. i.e. Add the distributed value of da. (≈1 line)
                        dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += distribute_value(da, shape)

    ### END CODE ###

    # Making sure your output shape is correct
    assert(dA_prev.shape == A_prev.shape)

    return dA_prev


######################################3

np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)

dA_prev = pool_backward(dA, cache, mode = "max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])  
print()
dA_prev = pool_backward(dA, cache, mode = "average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1]) 

# mode = max
# mean of dA =  0.145713902729
# dA_prev[1,1] =  [[ 0.          0.        ]
#  [ 5.05844394 -1.68282702]
#  [ 0.          0.        ]]

# mode = average
# mean of dA =  0.145713902729
# dA_prev[1,1] =  [[ 0.08485462  0.2787552 ]
#  [ 1.26461098 -0.25749373]
#  [ 1.17975636 -0.53624893]]

恭喜你！完成了这个作业，现在你已经掌握了卷积神经网络的工作原理和步骤。接下来我们将通过TensorFlow框架实现ConvNet

Part 2：卷积神经网络: 应用

利用TensorFlow实现ConvNet

0 TensorFlow 模型

导包

import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
import tensorflow as tf
from tensorflow.python.framework import ops
from cnn_utils import *

%matplotlib inline
np.random.seed(1)

导入数据（手势）

# Loading the data (signs)
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

一共六种手势：0-5

查看数据

# Example of a picture
index = 6
plt.imshow(X_train_orig[index])
print ("y = " + str(np.squeeze(Y_train_orig[:, index])))

# y = 2

之前在第二课的时候，我们采用全连接实现了手势识别，不过图片的分类自然更适合用卷积神经网络了。

检查数据

X_train = X_train_orig/255.
X_test = X_test_orig/255.
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}

# number of training examples = 1080
# number of test examples = 120
# X_train shape: (1080, 64, 64, 3)
# Y_train shape: (1080, 6)
# X_test shape: (120, 64, 64, 3)
# Y_test shape: (120, 6)

1 创建占位符

为输入数据X和输出数据Y创建占位符

• X (None, n_H0, n_W0, n_C0) : 第一个元素，尚未指定样本数量
• Y (None, n_y) : 第一个元素，尚未指定样本数量

# GRADED FUNCTION: create_placeholders

def create_placeholders(n_H0, n_W0, n_C0, n_y):
    """
    Creates the placeholders for the tensorflow session.

    Arguments:
    n_H0 -- scalar, height of an input image
    n_W0 -- scalar, width of an input image
    n_C0 -- scalar, number of channels of the input
    n_y -- scalar, number of classes

    Returns:
    X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype "float"
    Y -- placeholder for the input labels, of shape [None, n_y] and dtype "float"
    """

    ### START CODE HERE ### (≈2 lines)
    X = tf.placeholder(tf.float32, shape=[None, n_H0, n_W0, n_C0])
    Y = tf.placeholder(tf.float32, shape=[None, n_y])
    ### END CODE HERE ###

    return X, Y


#########################################

X, Y = create_placeholders(64, 64, 3, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))

# X = Tensor("Placeholder:0", shape=(?, 64, 64, 3), dtype=float32)
# Y = Tensor("Placeholder_1:0", shape=(?, 6), dtype=float32)

2 初始化参数

• W1: 权重(weight)
• W2: 卷积核(filter)

提示

在TensorFlow中为大小为[1,2,3,4]的W进行初始化

W = tf.get_variable("W", [1,2,3,4], initializer = ...)

# GRADED FUNCTION: initialize_parameters

def initialize_parameters():
    """
    Initializes weight parameters to build a neural network with tensorflow. The shapes are:
                        W1 : [4, 4, 3, 8]
                        W2 : [2, 2, 8, 16]
    Returns:
    parameters -- a dictionary of tensors containing W1, W2
    """

    tf.set_random_seed(1)                              # so that your "random" numbers match ours

    ### START CODE HERE ### (approx. 2 lines of code)
    W1 = tf.get_variable("W1", [4, 4, 3, 8], initializer=tf.contrib.layers.xavier_initializer(seed=0))
    W2 = tf.get_variable("W2", [2, 2, 8, 16], initializer=tf.contrib.layers.xavier_initializer(seed=0))
    ### END CODE HERE ###

    parameters = {"W1": W1,
                  "W2": W2}

    return parameters


###########################################3

tf.reset_default_graph()
with tf.Session() as sess_test:
    parameters = initialize_parameters()
    init = tf.global_variables_initializer()
    sess_test.run(init)
    print("W1 = " + str(parameters["W1"].eval()[1,1,1]))
    print("W2 = " + str(parameters["W2"].eval()[1,1,1]))


# W1 = [ 0.00131723  0.14176141 -0.04434952  0.09197326  0.14984085 -0.03514394
#  -0.06847463  0.05245192]
# W2 = [-0.08566415  0.17750949  0.11974221  0.16773748 -0.0830943  -0.08058
#  -0.00577033 -0.14643836  0.24162132 -0.05857408 -0.19055021  0.1345228
#  -0.22779644 -0.1601823  -0.16117483 -0.10286498]

3 前向传播

以下几个TensorFlow内置的方法可以帮你执行卷积的步骤

• tf.nn.conv2d(X,W1, strides = [1,s,s,1], padding = ‘SAME’)
  
  • 第一个参数：输入input
  • 第二个参数：多个卷积核(filters)
  • 第三个参数：输入的维度[m, n_H_prev, n_W_prev, n_C_prev]
• tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = ‘SAME’)
  
  • 第一个参数：池化层的输入(也就是卷几层的输出)
  • 第二个参数：窗口维度 [m, f, f, n_C_prev]
  • 第三个参数：步幅维度 [m, s, s, n_C_prev]
  • 第四个参数：padding模式
• tf.nn.relu(Z1)
  
  • 计算Z1的Relu: 各个元素分别计算
• tf.contrib.layers.flatten(P)
  
  • P[batchSize, …]为输入，batchSize为样本个数，将向量(除第一维)展开为一维向量，最后为二维向量 [batch_size, k]
• tf.contrib.layers.fully_connected(F, num_outputs)
  
  • 将输入的flatten向量运用全连接层到输出层，输出层节点个数为num_outputs，中间的各个参数由框架自己初始化和训练学习

练习

实现前向传播：CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

步骤如下：

• Conv2D: stride=1, padding=“SAME”
• ReLU
• Max pool: filter=[1,8,8,1], stride=[1,8,8,1] , padding=“SAME”
• Conv2D: stride=1, padding=“SAME”
• ReLU
• Max pool: filter=[1,4,4,1], stride=[1,4,4,1] , padding=“SAME”
• Flatten
• FULLYCONNECTED (FC) 全连接层
  
  • 注意全连接层并没有加非线性部分(比如softmax)，这是因为在TensorFlow框架中，非线性部分将在计算cost时调用，而不是这里

# GRADED FUNCTION: forward_propagation

def forward_propagation(X, parameters):
    """
    Implements the forward propagation for the model:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "W2"
                  the shapes are given in initialize_parameters

    Returns:
    Z3 -- the output of the last LINEAR unit
    """

    # Retrieve the parameters from the dictionary "parameters" 
    W1 = parameters['W1']
    W2 = parameters['W2']

    ### START CODE HERE ###
    # CONV2D: stride of 1, padding 'SAME'
    Z1 = tf.nn.conv2d(X, W1, strides=[1,1,1,1], padding='SAME')
    # RELU
    A1 = tf.nn.relu(Z1)
    # MAXPOOL: window 8x8, sride 8, padding 'SAME'
    P1 = tf.nn.max_pool(A1, ksize=[1,8,8,1], strides=[1,8,8,1], padding='SAME')
    # CONV2D: filters W2, stride 1, padding 'SAME'
    Z2 = tf.nn.conv2d(P1, W2, strides=[1,1,1,1], padding='SAME')
    # RELU
    A2 = tf.nn.relu(Z2)
    # MAXPOOL: window 4x4, stride 4, padding 'SAME'
    P2 = tf.nn.max_pool(A2, ksize=[1,4,4,1], strides=[1,4,4,1], padding='SAME')
    # FLATTEN
    P2 = tf.contrib.layers.flatten(P2)
    # FULLY-CONNECTED without non-linear activation function (not not call softmax).
    # 6 neurons in output layer. Hint: one of the arguments should be "activation_fn=None" 
    Z3 = tf.contrib.layers.fully_connected(P2, 6, activation_fn=None)
    ### END CODE HERE ###

    return Z3


##########################################

tf.reset_default_graph()

with tf.Session() as sess:
    np.random.seed(1)
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    init = tf.global_variables_initializer()
    sess.run(init)
    a = sess.run(Z3, {X: np.random.randn(2,64,64,3), Y: np.random.randn(2,6)})
    print("Z3 = " + str(a))

# Z3 = [[-0.44670227 -1.57208765 -1.53049231 -2.31013036 -1.29104376  # 0.46852064]
#  [-0.17601591 -1.57972014 -1.4737016  -2.61672091 -1.00810647  0.5747785 ]]

3 计算代价函数 cost

提示

• tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y)
  
  • 计算softmax层次的损失函数，包含输出的非线性部分和结果的损失计算
• tf.reduce_mean
  
  • 跨维度计算各个元素的均值

# GRADED FUNCTION: compute_cost 

def compute_cost(Z3, Y):
    """
    Computes the cost

    Arguments:
    Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
    Y -- "true" labels vector placeholder, same shape as Z3

    Returns:
    cost - Tensor of the cost function
    """

    ### START CODE HERE ### (1 line of code)
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y))
    ### END CODE HERE ###

    return cost


######################################3

tf.reset_default_graph()

with tf.Session() as sess:
    np.random.seed(1)
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    cost = compute_cost(Z3, Y)
    init = tf.global_variables_initializer()
    sess.run(init)
    a = sess.run(cost, {X: np.random.randn(4,64,64,3), Y: np.random.randn(4,6)})
    print("cost = " + str(a))

# cost = 2.91034

4 模型

集成上述各部分来建立模型，在手势数据集上进行训练。

完成下列方法：

• create placeholders
• initialize parameters
• forward propagate
• compute the cost
• create an optimizer

最后我们创建session并在每个epoch和mini-batch上执行模型。

# GRADED FUNCTION: model

def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,
          num_epochs = 100, minibatch_size = 64, print_cost = True):
    """
    Implements a three-layer ConvNet in Tensorflow:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

    Arguments:
    X_train -- training set, of shape (None, 64, 64, 3)
    Y_train -- test set, of shape (None, n_y = 6)
    X_test -- training set, of shape (None, 64, 64, 3)
    Y_test -- test set, of shape (None, n_y = 6)
    learning_rate -- learning rate of the optimization
    num_epochs -- number of epochs of the optimization loop
    minibatch_size -- size of a minibatch
    print_cost -- True to print the cost every 100 epochs

    Returns:
    train_accuracy -- real number, accuracy on the train set (X_train)
    test_accuracy -- real number, testing accuracy on the test set (X_test)
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    ops.reset_default_graph()                         # to be able to rerun the model without overwriting tf variables
    tf.set_random_seed(1)                             # to keep results consistent (tensorflow seed)
    seed = 3                                          # to keep results consistent (numpy seed)
    (m, n_H0, n_W0, n_C0) = X_train.shape             
    n_y = Y_train.shape[1]                            
    costs = []                                        # To keep track of the cost

    # Create Placeholders of the correct shape
    ### START CODE HERE ### (1 line)
    X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
    ### END CODE HERE ###

    # Initialize parameters
    ### START CODE HERE ### (1 line)
    parameters = initialize_parameters()
    ### END CODE HERE ###

    # Forward propagation: Build the forward propagation in the tensorflow graph
    ### START CODE HERE ### (1 line)
    Z3 = forward_propagation(X, parameters)
    ### END CODE HERE ###

    # Cost function: Add cost function to tensorflow graph
    ### START CODE HERE ### (1 line)
    cost = compute_cost(Z3, Y)
    ### END CODE HERE ###

    # Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
    ### START CODE HERE ### (1 line)
    optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
    ### END CODE HERE ###

    # Initialize all the variables globally
    init = tf.global_variables_initializer()

    # Start the session to compute the tensorflow graph
    with tf.Session() as sess:

        # Run the initialization
        sess.run(init)

        # Do the training loop
        for epoch in range(num_epochs):

            minibatch_cost = 0.
            num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
            seed = seed + 1
            minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)

            for minibatch in minibatches:

                # Select a minibatch
                (minibatch_X, minibatch_Y) = minibatch
                # IMPORTANT: The line that runs the graph on a minibatch.
                # Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
                ### START CODE HERE ### (1 line)
                _ , temp_cost = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
                ### END CODE HERE ###

                minibatch_cost += temp_cost / num_minibatches


            # Print the cost every epoch
            if print_cost == True and epoch % 5 == 0:
                print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
            if print_cost == True and epoch % 1 == 0:
                costs.append(minibatch_cost)


        # plot the cost
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        # Calculate the correct predictions
        predict_op = tf.argmax(Z3, 1)
        correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))

        # Calculate accuracy on the test set
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
        print(accuracy)
        train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
        test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
        print("Train Accuracy:", train_accuracy)
        print("Test Accuracy:", test_accuracy)

        return train_accuracy, test_accuracy, parameters


############################################

_, _, parameters = model(X_train, Y_train, X_test, Y_test)

# Cost after epoch 0: 1.917929
# Cost after epoch 5: 1.506757
# Cost after epoch 10: 0.955359
# Cost after epoch 15: 0.845802
# Cost after epoch 20: 0.701174
# Cost after epoch 25: 0.571977
# Cost after epoch 30: 0.518435
# Cost after epoch 35: 0.495806
# Cost after epoch 40: 0.429827
# Cost after epoch 45: 0.407291
# Cost after epoch 50: 0.366394
# Cost after epoch 55: 0.376922
# Cost after epoch 60: 0.299491
# Cost after epoch 65: 0.338870
# Cost after epoch 70: 0.316400
# Cost after epoch 75: 0.310413
# Cost after epoch 80: 0.249549
# Cost after epoch 85: 0.243457
# Cost after epoch 90: 0.200031
# Cost after epoch 95: 0.175452

# Tensor("Mean_1:0", shape=(), dtype=float32)
# Train Accuracy: 0.940741
# Test Accuracy: 0.783333

思考

你可以试着识别”赞”的手势

fname = "images/thumbs_up.jpg"
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64))
plt.imshow(my_image)