JPEG算法分析与实现
这是前面自己做的很low的一个作业,闲来无事第一次写东西也不知道写什么,就拿这个作业开头吧!如有错误望见谅并且指出!!
一、简单的引言还是要有的
JPEG是第一个国际图像压缩标准,用于连续色调静态图像(即包括灰度图像和彩色图像)。JPEG是联合图像专家组(JointPhotographic Experts Group)的缩写,这个图像压缩标准是国际化电信联盟(ITU)、国际化标准化组织(ISO)和国际电工委员会(IEC)合作努力的结果。JPEG标准正式地称为ISO/IECIS(国际标准)10918-1:连续色调静态图像数字压缩和编码和ITU-T建议T.81。JPEG标准的目的在于支持用于大多数连续色调静态图像压缩的各种各样的应用,这些图像可以是任何一个色彩空间,用户可以调制压缩比,并能达到或者接近技术领域中领先的压缩性能,且具有良好的重建质量。这个标准的另一个目标是对普遍实际的应用提供易处理的计算复杂度。在ISO公布的JPEG标准方案中,JPEG包含了两种压缩方式。一种是基于DCT变换的有损压缩编码方式,它包含了基本功能和拓展系统两部分;另一种是基于空间DPCM(差分脉冲编码调制)方法的无损压缩编码方式。本文实现的是第一种中的基本功能部分,即baseline部分。
二、数字图像压缩综述
1、数字图像压缩原理
图像压缩是指以较少的比特有损或无损地表示原来的像素的技术,也称图像编码。图像数据之所以能够被压缩,就是因为图像数据中存在着冗余。图像数据中通常的冗余信息包括以下几种:
(1)空间冗余:是指图像的相邻像素或相邻行之间存在较强的空域相关性。也就是说在一幅图像中均匀区域上的像素值变化是非常小的;
(2) 时间冗余:主要是指在视频图像序列中,相邻帧图像之间存在非常强的相关性;
(3)频谱冗余:是由不同彩色平面或频谱带的相关性引起的冗余;
(4)编码冗余:通常,图像各像素点灰度值并不是等概率分布的,也就是说各灰度值数据的信息熵是不同的,如果每个像素数据都用相同的比特数表示,必然存在编码冗余;
(5)视觉冗余:视觉冗余是相对于人眼的视觉特性而言的,人类的视觉系统对图像的各部分变化的敏感程度是不同的,例如对亮度的变化敏感,对色度的变化相对不敏感。
图像压缩编码的就是要出去这些冗余信息,在某些应用中,一定程度的失真是允许的,因此也就可以对图像做一定程度甚至是很大程度的有损压缩。
2、数字图像压缩的分类
2.1无损压缩
所谓无损压缩,就是利用数据的统计冗余来进行压缩,解压的时候可以完全恢复原始数据而不引起任何失真,但压缩率受到数据统计冗余度的理论限制,通常压缩率都非常低。图像的无损压缩通常分为两步,即去相关和编码。在无损压缩的编码设计过程中,采用的都是变长编码,也就是根据数据出现的概率分配不同长度的编码,对于那种出现概率很高的数据分配短的编码,对于出现概率很低的数据分配较长的编码,这样编码的位数不是固定的,而且总的平均码长较低,达到数据压缩的目的。图像压缩的过程中主要用到的有以下几种变长编码:
(1)霍夫曼编码。其基本思想是将整幅图像像素数据扫描一遍,统计各像素出现的概率,按照出现的概率大小来为其分配唯一的编码。通过这样的方式就可以构造出一幅图像的霍夫曼表,而且通过这样构造出来的编码的平均码长一定是最短的;
(2)行程编码(RLE)。又称游程编码、行程长度编码等,也是一种统计编码。编码的主要思想就是检测重复的比特或字符序列,并用它们的出现次数取而代之,这图像压缩的应用过程中,这样的重复比特通常指“0”;
(3)算术编码。是一种熵编码的方法,其特点在于其他的熵编码方法通常是把输入的消息分割为符号,然后对每个符号进行编码,而算术编码是直接把整个输入的消息编码为一个数,一个满足(0《n《10)的小数n。
2.2 有损压缩
有损压缩又称为破坏型压缩,利用了人类视觉系统对图像中的某些频率成分不敏感的特性,允许压缩过程中损失一定的信息;虽然不能完全恢复原始数据,但是所损失的部分对理解原始图像的影响很小,却换来了比无损压缩大得多的压缩比。在图像压缩的过程中通常用到的有预测编码和变换编码等。预测编码是根据离散信号之间存在着一定关联性的特点,利用前面一个或多个信号预测下一个信号,然后对实际值和预测值的差进行编码;变换编码就是空域的图像信号变换到频域进行处理,变换到频域以后会产生一批变换系数,然后对这些变换系数进行量化和编码。常用的变换有DCT(离散余弦变换)、DFT(离散傅里叶变换)、WHT(WalshHadama变换)等,其中最常用的是DCT(离散余弦变换)。
3.压缩效果的评价
图像的内容不都是相同的,在不同的压缩条件下,不同的压缩方法下压缩后的图像质量也是参差不齐,这就需要对压缩后的图像质量进行正确的评价,目前常用的评价方法主要有两种,即客观质量评价和主观质量评价。
(1)主观的质量评价就是让观察者对同一幅图像按照直观的视觉效果进行打分,然后求其加权平均,这种评价的标准符合人眼的视觉直观感受,但是观察者个体影响较大,而且使用起来不方便,不能用数学模型对其进行描述,不能直接用于图像编码过程中的质量评价和控制,所以普遍采用的是利用客观的评价方法对图像质量进行评价。
(2)客观评价方法是用重建后的图像偏离原始图像的误差来衡量图像恢复的质量,最常用的有均方误差(MSE)和峰值信噪比(PSNR)。均方误差法首先计算原始图像和失真图像像素差值的均方值,然后通过均方值的大小来确定失真图像的失真程度,计算公式如所示;峰值信噪比作为衡量图像质量的重要指标,基于通信理论而提出,是最大信号量与噪声强度的比值,在图像中这里的最大信号量指的是图像的最大像素值,计算公式如下所示。
4、JPEG算法分析与实现
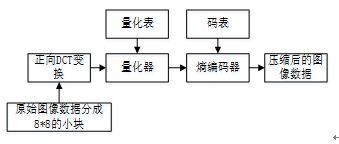
JPEG定义了两种基本的压缩算法,一种是基于DCT变换的有损压缩算法,包括基本(Baseline)系统和扩展系统;另外一种是基于DPCM(差分脉冲编码调制)的无损压缩算法,又称Spatial方式,这种方式下压缩后的图像是可以完全复原重建的,但是这也意味着在无损压缩下压缩比非常的低,通常在10:1以下。本文分析实现的算法是基于DCT变换的基本系统,编码过程如图所示,主要分成了五个部分。以下将从五个模块分别介绍详细各个模块的原理与实现过程。
4.1 颜色空间转换与图像分割
4.1.1 颜色空间转换
颜色空间也称彩色模型(又称彩色空间或彩色系统),用于在某些标准下用通常可接受的方式对彩色加以说明。不同的颜色空间有不同的应用场景,例如常见的有RGB、CMYK和YCbCr等。其中YCbCr模型中的Y表示亮度,Cb和Cr表示色差,在图像或者视频压缩的过程中,第一步就是需要将RGB表示的图像转换成YCbCr表示。用YCbCr模型表示有很多好处,一是利用人眼对图像的亮度信息的敏感度高于色差信息,这样在压缩的过程中就可以更好的保留人眼视觉系统能感知的部分,而对色差部分的压缩程度相对会大很多;二是早期为了兼顾黑白电视机,因为黑白电视机只需要Y分量的信息就可以工作。下面直接给出从RGB到YCbCr的转换公式(2)。
其中,R,G,B表示的是原始RGB图像的红绿蓝通道分别的值。图2所示就是转换到YCbCr通道的效果图,YCbCr模型有三种存储方式,分别是4:2:0、4:2:2和4:4:4,本实验使用的是4:4:4的方式(其实这个地方我没搞清楚。。。)。
4.1.2 图像块分割
在转换到YCbCr颜色空间后,还有一步工作就是图像的分块,本实验将图像分成8*8(像素)的块,实验中的测试图像大小只包含了8*8、16*16、32*32、64*64、128*128和256*256,不考虑不能被8整除的图像。后面所有的编码工作都是在每一个8*8块上分别进行的。
4.2 DCT变换与量化
4.2.1 DCT变换
离散余弦变换(DiscreteCosine Transform,简称DCT)是一种与傅里叶变换紧密相关的数学运算,在傅里叶级数展开式中,如果被展开的函数是实偶函数,那么其傅里叶级数中只包含余弦项,再将其离散化可导出余弦变换,因此称之为离散余弦变换。
之所以选择DCT变换将图像从空域变换到频域进行处理,是因为DCT是正交变换,它可以将8*8的空间表达式转换为频率域,只需要用少量的数据点就可以表示图像;DCT产生的系数很容易被量化,因此能获得好的块压缩;DCT算法是对称的,所以利用逆DCT算法可以用来解压缩图像。实验中用的二维DCT变换和逆变换的计算公式如下所示(采用8*8的块)。
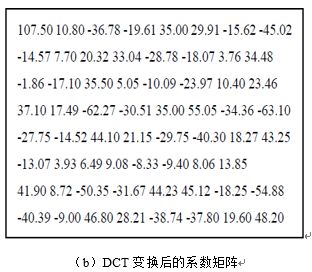
图3所示是实验中的8*8图像大小的块的Y通道的DCT变换前的像素值和DCT变换后的DCT系数矩阵。
DCT将8*8图像块变换为频率域时数值集中在矩阵左上角,即低频分量都集中在左上角,高频分量分布在右下角。由于该低频分量包含了图像的主要信息,而高频与之相比就不那么重要了,高频分量主要表示的是图像的细节信息,所以可对高频分量进行很大程度的处理,以此来减小数据量,达到数据压缩的目的。
4.2.2 量化
量化是对经正向DCT变换后的频率系数进行处理以增加零系数的数目。量化是对DCT系数进行压缩的最为关键的一步,方法是通过降低DCT系数精度的方法,去除掉图像中相对不重要的表示图像细节的AC系数,也就是图像中分布在右下角的高频分量,从而减少图像数据量,量化是压缩中图像质量下降的最主要原因,并且量化是破坏性的、不可逆的。
在JPEG中,使用的是线性均匀量化器,量化定义为对64个DCT系数除以量化步长,然后取整,如公式4所示。在降低精度中,删除掉离DC系数较远的值,即AC系数,这样DCT系数的精度降低了,目标是以不超出达到期望图像质量所必须的精度来表示DCT系数。
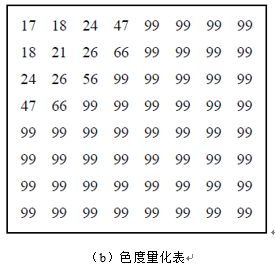
量化后的系数是用DCT输出矩阵除以量化矩阵得到的结果,量化矩阵含有量化量化值,也称作步长。如公式(4)所示,其中的 是量化值做分母,如果它是1,量化后的系数就具有较高的精度,随着量化值增大,量化后的系数的精度就降低。JPEG算法包括一套量化表,它们是从广泛的实验中得出的。量化表对人眼敏感的亮度信息部分采用细量化,对色差信息进行粗量化,所以就有两张量化表,一张是针对Y分量的,一张是针对Cb和Cr分量的,在实际应用过程中,也可以自行定义量化表,本次实验使用的是官方推荐的量化表,如图4所示。
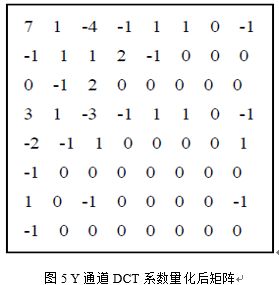
图5所示的是在图3(b)中的DCT系数矩阵量化后的结果,从图中可以看到,在量化之后,8*8矩阵中大多数量化后的DCT系数都被截取为零值。
4.3 差值脉冲编码与行程编码
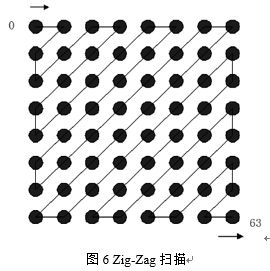
4.3.1 Z扫描
为了保证低频分量先出现,高频分量后出现,以增加行程中连续“0”的个数,对每个量化后的8*8的系数矩阵采用Zig-Zag扫描排列,扫描的方法如图6所示。
按图6所示的扫描规则,就可以将每个8*8二维矩阵转换成一维数组存储,而且连续“0”的个数明显增加,如图5的矩阵经过Zig-Zag扫描后变为一维数组:[7,1,-1,0,1,-4,-1,1,-1,3,-2,1,2,2,1,1,-1,0,-3,-1,-1,1,0,1,-1,0,0,0,-1,0,0,1,0,0,0,-1,0,-1,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,-1,0,0]。
4.3.2 DC和AC系数分别编码
(1)DC系数编码。前面已经介绍过,在经过DCT变换以后,低频分量主要集中在左上角,其中的F(0,0)表示直流分量,需要进行单独编码。由于相邻的8*8块间直流系数的变化较小,所以用差分编码DPCM对直流分量进行编码,即对差值DIFF=D(i)-D(i-1)进行编码,从而提高压缩比。
(2)AC系数编码。AC系数的编码采用行程编码(RLE),即对于连续重复出现的字符记录字符出现的次数即可,在JPEG中,可以看到出现大量重复的零值,所以RLE编码后可以记录为(非零字符前的零字符出现次数,非零字符)。所以上一节经过Zig-Zag扫描后形成的一维数组经过行程编码后变成了如下的序列:[(0,7),(0,1),(0,-1),(1,1),(0,-4),(0,-1),(0,1),(0,-1),(0,3),(0,-2),(0,1),(0,2),(0,2),(0,1),(0,1),(0,-1),(1,-3),(0,-1),(0,-1),(0,1),(1,1),(0,-1),(3,-1),(2,1),(3,-1),(1,-1),(2,1),(1,1),(10,-1),(0,1),(6,-1),EOB],其中的EOB符号表示后面剩下的字符都是零字符。
4.4 霍夫曼编码
经过上一节已经经过行程编码的序列,为了进一步的压缩,需要再次进行熵编码,JPEG标准具体规定了两种熵编码方式,即Huffman编码和算术编码。JPEG基本顺序编码解码器具体规定用Huffman编码,但JPEG并没有限制对任何JPEG算法必须用Huffman编码方式或算术编码方式,本次实验使用的是Huffman编码,主要分成两步进行,首先把DC码和行程码转换成中间符号序列,然后再对这些符号进行编码,赋以不同的变长码字。
4.4.1 编码理论基础
哈夫曼编码是1952年由Huffman提出的一种编码方法。这种编码方法的主要思想是根据源数据符号出现的概率进行编码,出现概率越高的符号,分配越短的编码,反之,分配以较长的编码,从而达到用尽可能少的编码符号表示数据源。Huffman编码的步骤如下:
(1) 统计一幅图像中各个像素值出现的概率;
(2)将信源符号按概率递减顺序进行排列,若出现概率相等时,次序可依次排列就行;
(3) 把两个最小概率相加作为新符号的概率,新符号获得一个新的概率,即前面两个概率的和,然后将新符号按照(2)重排;
(4) 重复(1)和(2)步骤,直到最后两个符号的概率之和为1,并且将概率为1的新符号也需要列出来;
(5) 在每次合并信源时,将合并的信源分别赋字符“0”和字符“1”;
(6) 寻找从每一信源符号到概率为1处的路径,记录路径上的“1”和“0”;
(7) 写出每一符号的“1”、“0”序列(从树根到信源符号节点)。
4.4.2 编码实现
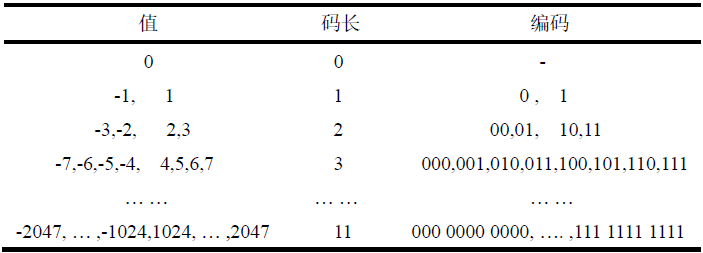
为了获得最后编码后的二进制流表示,首先需要对经过RLE编码后的序列中括号里的非零分量的值进行二进制编码,JPEG提供了一张标准的码表用于对这些数字进行编码,如表1所示,表中记录了编码结果,以及编码的码长。
按照表1中的编码规则对RLE编码后的序列进行编码,编码后的序列如下:[(0,3,111),(0,1,1),(0,1,0),(1,1,1),(0,3,011),(0,1,0),(0,1,1),(0,1,0),(0,3,11),(0,2,01),(0,1,1),(0,2,10),(0,2,10),(0,1,1),(0,1,1),(0,1,0),(1,3,00),(0,1,0),(0,1,0),(0,1,1),(1,1,1),(0,1,0),(3,1,0),(2,1,1),(3,1,0),(1,1,0),(2,1,1),(1,1,1),(10,1,0),(0,1,1),(6,1,0),EOB]。
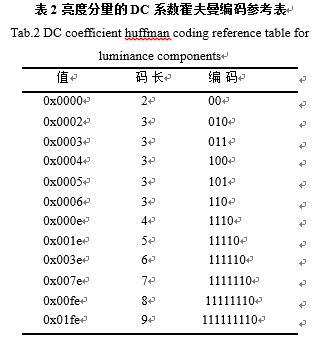
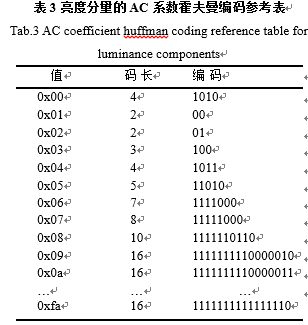
括号中前两个数字都在0到F之间,正好可以将两个数合并成一个字节,高4位是前面0的个数,后四位是后面数字的位数。对于合并这个后的字节,就需要进行最后的霍夫曼编码了,在JPEG的标准中一共提供了四张霍夫曼编码的参考表,分别是亮度分量的DC和AC编码表,还有色差分量的DC和AC编码表。表2所示的是亮度分量DC分量的霍夫曼编码表,表3所示的是色差分量AC分量的霍夫曼编码表。
在JPEG标准中提供了四张霍夫曼编码的参考表,表2和表3表示的只是亮度分量的编码表,色差分量的在这里没有列出,具体可以参考JPEG标准。如经过霍夫曼编码,上一节的8*8块的Y分量最后的编码结果也就是最后的二进制序列为:1001110010001100110001100000100010011010100101100110001001000111100100000000001110010001110100111001111010011000111001110011111110100001111101101010。至此,JPEG基本系统的编码算法以及实现细节已经介绍完毕,也就是数据的压缩在这里已经完成,最后的格式封装将在下一节进行介绍。
4.5 JPEG封装格式简介
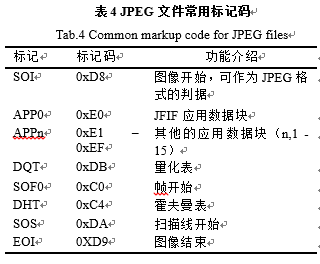
JPEG文件大体上可以分成以下两个部分:标记码和压缩数据。标记码由两个字节构成,其前一个字节是固定值0xFF,每个标记之前还可以添加数目不限的0xFF填充字节(fill byte)。标记码部分给出了JPEG图像的所有信息,如图像的宽、高、Huffman表、量化表等。标记码有很多,但绝大多数的JPEG文件通常只包含了表4所示的几种。
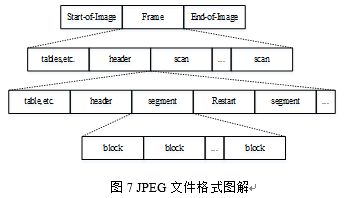
表4和图7只是给出了JPEG文件格式中最基本的内容介绍,实际的.jpeg或者.jpg文件格式分析,可以用文本编辑器打开对照着具体分析。在JPEG图像编码中,还经常用到的一个概念就是MCU,它表示的是最小编码单元,即Minimum Coding Unit,在实际的编码中,都是以一个一个的MCU为单位进行的。
0、总结吧
1、代码写得很陋。。。但是感动自己,还是放出来了,看了可以笑一笑:https://download.csdn.net/download/hello_next_day/10279706
2、在写作业的过程中主要参考的大神们的资料:
https://blog.csdn.net/newchenxf/article/details/51719597
https://blog.csdn.net/shelldon/article/details/54234433
还有这本书: