双目SLAM基础

双目slam基础 Stereo camera slam

Stereo Vision:Algorithms and Applications 双目宝典

Machine-learning-for-low-level-vision-problems 机器学习实现低层次视觉-深度估计等

室外数据集 Kitti

室内数据集 Middlebury 双目算法评估

嵌入式 图像滤波卷积计算 卷积的简化计算

双目 匹配 CRF平滑 后处理

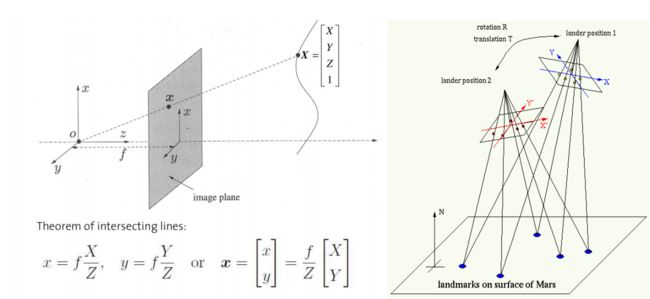
针孔相机模型 

0.基础知识 Basic Knowledge

相机内参数 Intrinsic parameters

内参数K 

    u         x     fx  0  cx
    v  =  K * y  =  0   fy cy   
    1         z     0   0   1

     * 相机感光元件CCD的尺寸是8mm X 6mm，
       帧画面的分辨率设置为640X480，
       那么毫米与像素点之间的转换关系就是80pixel/mm  80像素每毫米
     * CCD传感器每个像素点的物理大小为dx*dy，相应地，就有 dx=dy=1/80
     * 假设像素点的大小为k x l，其中 fx = f / k， fy = f / (l * sinA)， 
                                   fx = 80*焦距  fy = 80*焦距
                                   焦距为相机光心到感光平面中心的距离
       A一般假设为 90°，是指摄像头坐标系的偏斜度（就是镜头坐标和CCD是否垂直）。
     * 摄像头矩阵（内参）的目的是把图像的点从图像坐标转换成实际物理的三维坐标。
        因此其中的fx, fy, cx, cy 都是使用类似上面的纲量。
     * 同样，Q 中的变量 f，cx, cy 也应该是一样的。

                                                 |Xw|
     *   |u|    |fx  0   cx 0|     |  R   T |    |Yw|
     *   |v| =  |0   fy  cy 0|  *  |        | *  |Zw| = M * W
     *   |1|    |0   0   1  0|     | 0 0 0 1|    |1 |

     *   像素坐标齐次表示(3*1)  =  内参数矩阵 齐次表示 3*4  ×  外参数矩阵齐次表示 4*4 ×  物体世界坐标 齐次表示  4*1
     *   内参数齐次 × 外参数齐次 整合 得到 投影矩阵M  3*4    
     *   对于左右两个相机 投影矩阵 P1=M1   P2=M2
     *    世界坐标　W 　---->　左相机投影矩阵 P1 ------> 左相机像素点　(u1,v1,1)
     *                 ----> 右相机投影矩阵 P２ ------> 右相机像素点　(u2,v2,1)

     以下更加三角测量可以得到：
     *   Q为 视差转深度矩阵 disparity-to-depth mapping matrix 

     * Z = f*B/d        =   f    /(d/B)    B为相机基线长度  d为两匹配像素的视差
     * X = Z*(x-cx)/fx = (x-c_x)/(d/B)     相似三角形
     * Y = Z*(y-cy)/fy = (y-c_x)/(d/B) 

     X        x
     Y  = Q * y
     Z        d
     1        1

     * Q= | 1   0    0         -c_x     |    Q03
     *    | 0   1    0         -c_y     |    Q13
     *    | 0   0    0          f       |    Q23
     *    | 0   0   -1/B   (c_x-c_x')/B |  
     *              Q32        Q33     

     c_x和c_x'　为左右相机　平面坐标中心的差值（内参数）

     *  以左相机光心为世界坐标系原点   左手坐标系Z  垂直向后指向 相机平面  
     *        |x|   | x-cx         |     |X'|
     *        |y|   | y-cy         |     |Y'|
     *   Q  * |d| = | f            |  =  |Z'| ====>归一化==>  Z = Z/W =  -f*B/(d-c_x+c_x')
     *        |1|   |(-d+cx-cx')/B |     |W |
     
     * Z = f * B/ D    f 焦距 量纲为像素点 B为双目基线距离   
     * 左右相机基线长度 量纲和标定时 所给标定板尺寸 相同 
     * D视差 量纲也为 像素点 分子分母约去，Z的量纲同 B
    Q 示例：
    [ 1., 0., 0., -3.3265590286254883e+02, 
      0., 1., 0., -2.3086411857604980e+02, 
      0., 0., 0., 3.9018919929094244e+02, 
      0., 0., 6.1428092115522364e-04, 0. ]

相机畸变参数 Extrinsic parameters

 r^2 = x^2+y^2
 * 径向畸变矫正 光学透镜特效  凸起                k1 k2 k3 三个参数确定
 * Xp=Xd(1 + k1*r^2 + k2*r^4 + k3*r^6)
 * Yp=Yd(1 + k1*r^2 + k2*r^4 + k3*r^6)
 
 * 切向畸变矫正 装配误差                         p1  p2  两个参数确定
 * Xp=Xd + ( 2 * p1 * y   +  p2 * (r^2 +2 * x^2) )
 * Yp=Yd + ( p1 * (r^2 + 2 * y^2) + 2 * p2 * x )

1. 双目相机校正Stereo Rectification

opencv双目校准 程序参考

    相对位置矩阵：
        R t 为 左相机到右相机 的 旋转与平移矩阵  
            R维度：3*3     
            t维度：3*1  
            t中第一个tx为 双目基线长度 
        
    摆正矩阵:   
        立体校正的时候需要两幅图像共面并且 行对准 以使得立体匹配更加的可靠 
        使得两幅图像共面的方法就是把两个摄像头的图像投影到一个 公共成像面上，
        这样每幅图像从本图像平面投影到 公共图像平面都需要一个旋转矩阵R 
        stereoRectify 这个函数计算的就是从图像平面投影都公共成像平面的旋转矩阵Rl,Rr。 
        Rl,Rr即为左右相机平面行对准的校正旋转矩阵。 
        左相机经过Rl旋转，右相机经过Rr旋转之后，两幅图像就已经共面并且行对准了。 
    投影矩阵：
        其中Pl,Pr为两个相机的投影矩阵，
        其作用是将3D点的坐标转换到图像的2D点的坐标:
        
            P*[X Y Z 1]' =[x y w]  
    重投影矩阵(视差转深度矩阵)：
     Q矩阵为重投影矩阵(视差转深度矩阵)，
     即矩阵Q可以把2维平面(图像平面)上的点投影到3维空间的点:
     
        Q*[x y d 1] = [X Y Z W]。
        
    其中d为左右两幅图像的视差. 

校准之后的效果

2. 特征提取 Feature Extraction

一个像素点进行匹配奇异性太大，所以需要对像素点计算特征之后，用像素点的特征来进行匹配
匹配之后可以得到视差，进而得到像素点的深度。

特征类型：
    1. 手工提取的特征(Hand-crafted feature )：
        a. 领域像素值信息：
            直接使用领域块像素值  
                绝对值误差和SAD 
                误差平方和SSD  
                相关性NCC(Normalized Cross Correlation 与块均值相关)
                STAD truncated absolute differences (TAD) 带最小阈值的 绝对值误差和
                sum(min(asb(),thresh))
            使用领域内像素相对信息 周围点相对于中心点像素值的大小关系 
                ORB特征 基于 Faster角点与BRIEF描述子。
                Faster角点特征：
                   半径为R的圆周上的像素点的亮度值与中心点的大小关系，大了就为1，小了就为0。
                BRIEF描述子：
                   邻域内随机选择n对像素点(p,q)，比较其灰度值大小，如果I(p)>I(q)，则令其对应的值为1，否则为0。
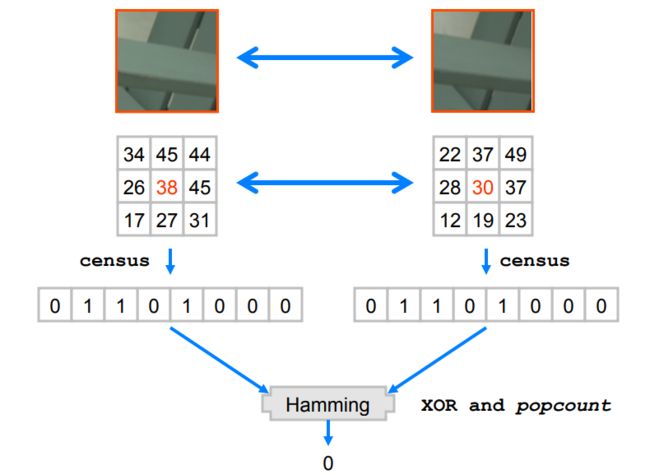
                Census变换特征：
                   在指定窗口内比较周围亮度值与中心点的大小，大了就为1，小了就为0，
                   然后每个像素都对应一个二值编码序列，然后通过海明距离来表示两个像素的相似程度。

        b. 领域像素梯度值信息：
            SIFT 尺度不变特征变换  对像素点领域内 像素梯度方向使用灰度梯度赋值加权统计。
            SURF 梯度的梯度信息 领域内使用赋值对方向加权统计。

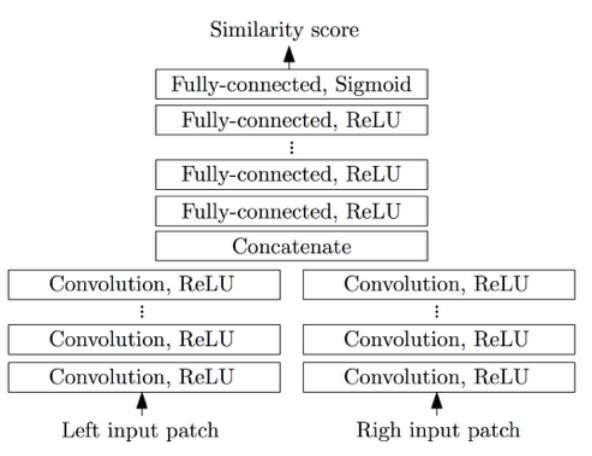
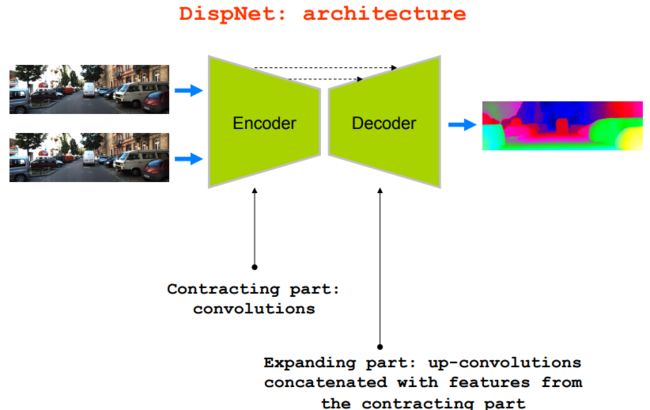
   2.  卷积网络提取的特征(Learnable feature from Conv-Nets)：
        输入 两张左右相机图像的图像块 到卷积网络(图片相似度判别网络Siamese network )内
             网络先对图像块进行特征提取，然后进行特征匹配，得到匹配代价图
        输出  matching cost匹配代价图
        更加匹配代价图，选出合适的匹配点，再计算视差，得到深度。
        网络形式在后面以图片形式放出。

Census计算代码

census计算示意图

相似性卷积网络1 卷积+全连接 

相似性卷积网络2 卷积+全连接

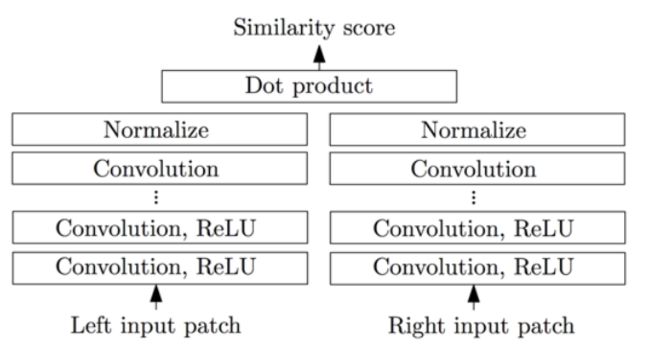
相似性卷积网络3 卷积+点乘ElementWise+全内容

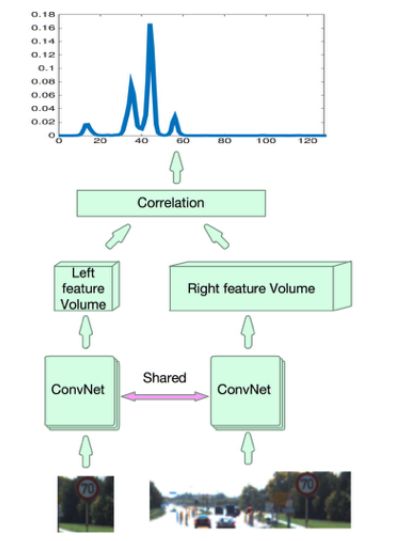
匹配误差cnn网络

端到端直接输出深度cnn网络

3. 双目特征匹配 Stereo Feature Matching

0.计算代价之前一般会预处理 对图像滤波

可使用 均值滤波/双边滤波/Census transform/高斯滤波等

a. 在极线范围内使用上面的特征计算方法计算 匹配代价Matching cost computation

sad差绝对值和

censun领域相对关系

双目匹配 极线范围内快匹配搜索

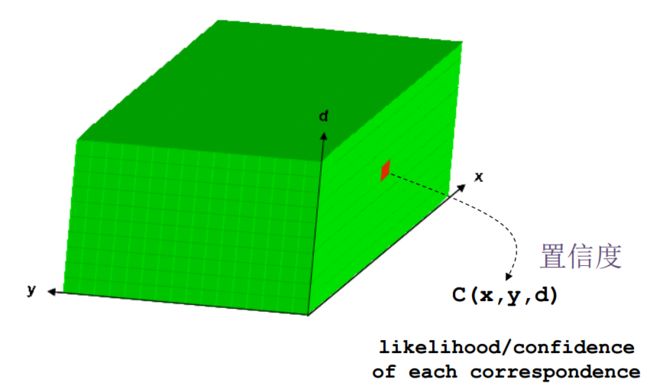
视差空间图像 Disparity Space Image (DSI) is a 3D matrix (WxHx(dmaxdmin)

b. 匹配代价聚合 Cost aggregation

场景内不同深度的代价不应该放在一起计算 可依据分割和像素值进行复权值 **多窗口 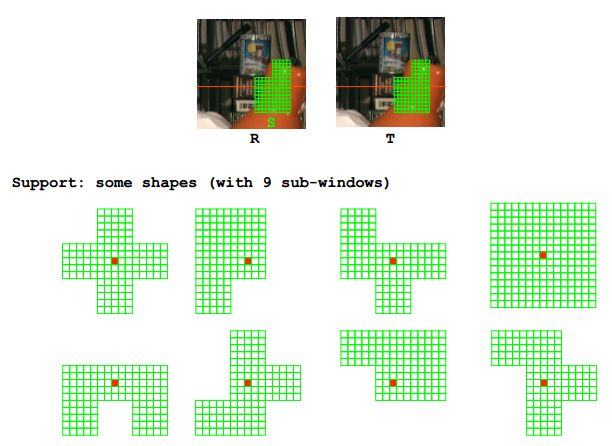 **图分割复权值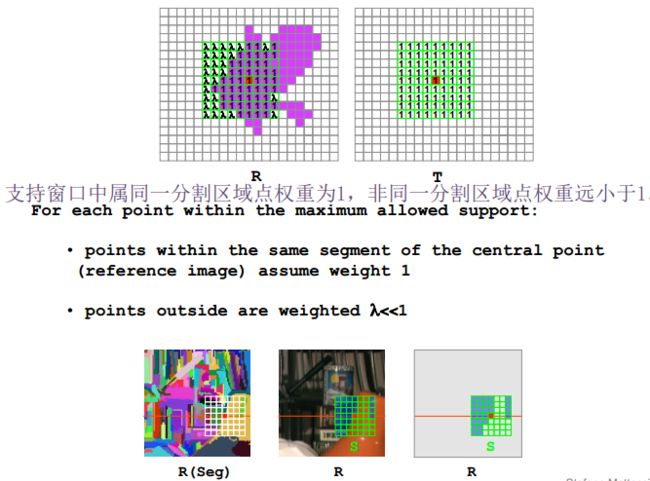 

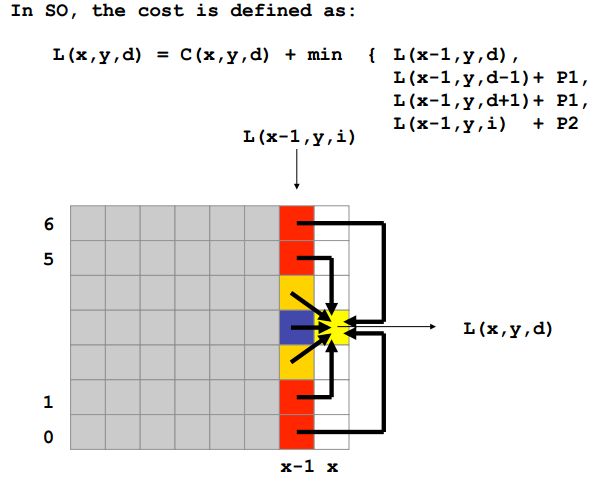
c. 视差计算&&优化 Disparity computation&&optimization

Scanline Optimization (SO) 线扫描优化

d. 视差细化调整 Disparity refinement 剔除外点

亚像素调整Sub-pixel interpolation

视差滤波

    中值滤波
    双边滤波

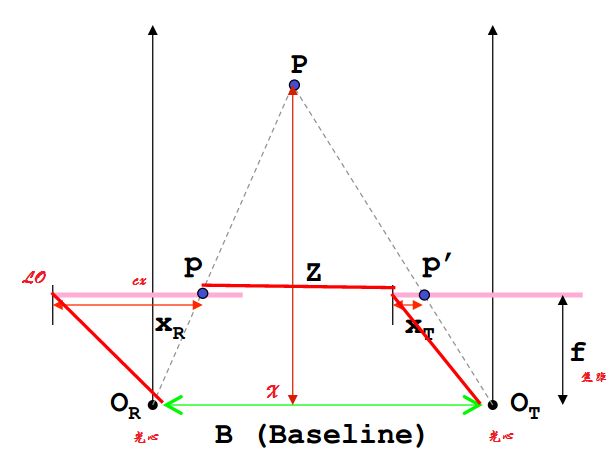
4. 三角测量得到深度 Triangulation

    上图中，三角形 P OR OT 相似于 三角形 P p p'
    更加相似三角形的对应边成比例定理：
    OR OT/ PX  = p p'/ PZ
    换成长度：
    B/Z  = (B+Xt-Xr) / (Z - f)
        B为基线长度值
        Z为点P的深度值
        f为相机焦距值
        Xr，Xt 为两幅图的匹配点坐标，Xr-Xt 为匹配点视差d
    化简可以得到：
    Z = B*f/(Xr-Xt) = B*f/d

    又有 三角形 OR cx p 相似于 三角形 P X OR
    得到：
    OR cx / p cx = P X / OR X
    换成长度：
    f/ (Xr - cx) = Z / X
    得到 ：
    X = Z/f * (Xr - cx)
    同理：
    Y = Z/f * (Yr - cy)

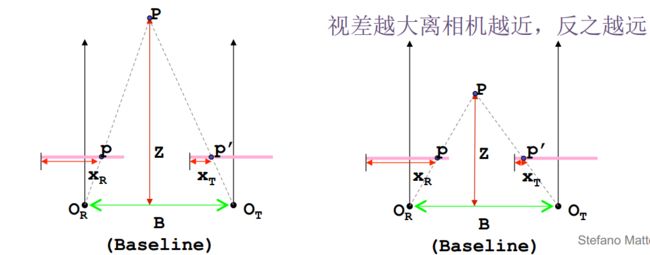
由于 Z =  B*f/d，
视差与深度成反比

深度估计总结

1. 主动方法

a. 结构光 Structured light  (Kinect1)  （iPhone X 齐刘海原理） Inter RealSenes
   光已知空间方向的投影光线的集合称为结构光，结构光激光散斑
   通过投射具有高度伪随机性的激光散斑，会随着不同距离变换不同的图案，
   对三维空间直接标记，通过观察物体表面的散斑图案就可以判断其深度。
b. ToF - Time of Flight飞行时间法  (Kinect2) 
   通过连续发射光脉冲（一般为不可见光）到被观测物体上，
   然后接收从物体反射回去的光脉冲，
   通过探测光脉冲的飞行（往返）时间来计算被测物体离相机的距离。
以上为RGBD传感器   
c. LIDAR 激光雷达    (Velodyne) 

结构光参考

飞行时间法

2.被动方法

a.  双目视觉
     上面介绍的
b. 基于机器学习的单目 深度传感器 Monocular depth* sensors based on ML
   需要先验知识

双目视觉博客参考

5. 相邻帧特征匹配 Temporal Feature Matching

使用双目 左右两幅图 立体匹配的到像素点对应的深度，进而得到3D点坐标
使用当前帧 和参考帧 (都使用左图) 匹配，恢复相机移动矩阵：
    1、在当前帧图像和参考帧图像寻找匹配点对(特征点匹配,光流法)
    2、计算变换矩阵的初始解
       参考帧2d点对应的3d点和 当前帧 2d点组成 3d-2d 匹配点对，使用PnP求解算法得到初始解
       或者使用 2d-2d变换求解算法(单应变换/本质矩阵)
    3、鲁棒优化位置矩阵
       使用RanSaC随机采样序列一致性算法,随机采样一些点对求解，计算剩余点对的误差，统计好的点的数量，选择内点数量多的变换关系
       或者使用最小二乘优化算法优化位置矩阵，使用误差加权的列文伯格马尔夸克算法W-LM更新位姿。
       
匹配点对计算方法，常见的有如下两种方式： 
    1. 计算特征点，然后计算特征描述子，通过描述子来进行匹配，优点准确度高，缺点是描述子计算量大。 
    2. 光流法：在第一幅图中检测特征点，使用光流法(Lucas Kanade method)对这些特征点进行跟踪，
       得到这些特征点在第二幅图像中的位置，得到的位置可能和真实特征点所对应的位置有偏差。
       所以通常的做法是对第二幅图也检测特征点，如果检测到的特征点位置和光流法预测的位置靠近，
       那就认为这个特征点和第一幅图中的对应。
       在相邻时刻光照条件几乎不变的条件下（特别是单目slam的情形），
       光流法匹配是个不错的选择，它不需要计算特征描述子，计算量更小。

光流计算

光流场景流
光流计算

假设1：光照亮度恒定：
                  I(x, y, t) =  I(x+dx, y+dy, t+dt) 
                 泰勒展开：
                  I(x+dx, y+dy, t+dt) =  
                                        I(x, y, t) + dI/dx * dx + dI/dy * dy + dI/dt * dt
                                      =  I(x, y, t) + Ix * dx  + Iy * dy + It * dt
                 得到：
                      Ix * dx  + Iy * dy + It * dt = 0
                 因为 像素水平方向的运动速度 u=dx/dt,  像素垂直方向的运动速度 v=dy/dt
                 等式两边同时除以 dt ,得到：
                      Ix * dx/dt  + Iy * dy/dt + It = 0
                      Ix * u  + Iy * v + It = 0
                 写成矩阵形式：
                      [Ix, Iy] * [u; v] = -It,  式中Ix, Iy为图像空间像素差值(梯度), It 为时间维度，像素差值
           假设2：局部区域 运动相同
                 对于点[x,y]附近的点[x1,y1]  [x2,y2]  , ... , [xn,yn]  都具有相同的速度 [u; v]
                 有：
                  [Ix1, Iy1;                      [It1
                   Ix2, Iy2;                       It2
                   ...               *  [u; v] = - ...
                   Ixn, Iyn;]                      Itn]
                 写成矩阵形式：
                  A * U = b
                 由两边同时左乘 A逆 得到：
                  U = A逆 * b
                 由于A矩阵的逆矩阵可能不存在，可以曲线救国改求其伪逆矩阵
                  U = (A转置*A)逆 * A转置 * b
           得到像素的水平和垂直方向速度以后，可以得到:
               速度幅值： 
                        V = sqrt(u^2 + v^2)
               速度方向：Cet = arctan(v/u)      

6. 姿态恢复/跟踪/随机采样序列 Incremental Pose Recovery/RANSAC

计算变换矩阵的初始解：
1、(单应变换/本质矩阵）求初始解

2d-2d变换求解算法(单应变换/本质矩阵) 单目里面有说过

2、3d-2d 匹配点对，使用PnP算法/直接线性变换DLT(6个 3D - 2D 点对) 得到初始解：
  a) 直接线性变换DLT:
        2D点-3Ｄ点对
        2d点通过内参数K 反变换到　归一化平面
         (u，v，1) 
        3d点其次表示　(X, Y, Z, 1) 
        变换矩阵：　T = [R t; 0 0 0 1] 维度　3*4
        s1为归一化尺度
        s1 * (u，v，1) = T * (X, Y, Z, 1)  = T * P 
        T = [t1 t2 t3 t4; 
             t5 t6 t7 t8; 
             t9 t10 t11 t12] = [T1; 
                                T2; 
                                T3]
         可得到 u = T1 × P/(T3 * P)   
             v =  T2 × P/(T3 * P) 
         移项可以得到:
               T3 * P *u - T1 * P =0 　 以及 
               T3 * P *v - T2 * P =0   
               每个3D - 2D 点对 可提供 两个约束
   T有 12个变量 至少需要6个 3D - 2D 点对 
   求解的 T的 左大半部分左上角３＊３
   不一定满足旋转矩阵R的约束关系（正交矩阵），
   得到 T后需要使用QR分解 使得得到的 T 满足 SE3
   用一个旋转矩阵去近似（将3*3矩阵空间投影到SE(3)流形上）
 上面也叫P6P
 
 b) PnP算法(P3P)，3点平面匹配: 
   世界坐标系下的ABC三点和图像坐标系下的abc三点匹配;
   其中AB，BC，AC的长度已知，，，也是已知，
   通过相似三角形余弦定理可以求出A，B，C在相机参考系中的3d坐标;
   原来就知道A, B, C 三点在世界坐标系下的坐标，现在有知道它们在相机坐标系下的坐标，
   进而可以转换成　3D-3D　点的匹配问题，使用 ICP算法求解       

3、3d-3d 匹配点对，使用ICP算法得到初始解：

ICP算法求解

    ICP：3D-3D点对求解变换矩阵
      使得 P2 = R* P1 + t
      线性代数求解  SVD奇异值分解方法
      求解 R,t 使得误差    ei = P2 - (R*P1 + t)
      利用最小二乘法求解最优解使：
      最小化误差和 min (1/n * sum(ei^2))   ; 
          e^2 = ei*ei转置
      得到 R t 

      先对平移向量T进行初始的估算，
         1) 具体方法是分别得到点集P1和P2的中心：
             p1 = 1/n * sum(P1)
             p2 = 1/n * sum(P2)
         2) 分别将点集P1和P2平移至中心点处：
             P1' = P1 - p1
             P2' = P2 - p2
         3) 误差变为：　ei' = (P2'+p2) - (R*(P1'+p1) + t)
           ei^2 =  (P1'- R*P2')^2 + (p2 - R*p1 - t)^2 
         4) 求 (P1'- R*P2')^2最小 可以得到R 
             (P1' - R * P2')^2 = 
             P1'转置*P1' - 2*P1'转置*R*P2'  + P2'转置*R转置*R*P2'  
             第一项与R无关 第三项 应为  R转置* R = I 与R也无关
             只剩下第二项　- 2*P1'转置*R*P2' 
             我们计算 B = P1'转置*P2'
             原最优化问题可以转为求B的最小特征值和特征向量
             对B进行奇异值分解得到:
                B = U * 对角矩阵 * V转置  
                R= U * V转置 
         5) 再求取转移矩阵t
           由　  P2 = R* P1 + t
            得到　t = P2 - R* P1     
鲁棒优化：
1、 使用RANSAC随机采样序列一致性算法
    随机采样一些点对求解，计算剩余点对的误差，统计好的点的数量，选择内点数量多的变换关系

2、最小二乘优化算法优化位置矩阵，使用误差加权的列文伯格马尔夸克算法W-LM更新位姿
    3D-2D点对匹配，最小化误差，求取误差函数对优化变量的偏导数，对优化变量进行更新

     三维点  Pi = (Xi, Yi, Zi)   相机坐标 pi = (xi, yi, 1)  像素坐标 ci = (ui, vi)  
     * 相机相对于  世界坐标系(第一帧图像相机) 的 旋转 平移矩阵 R t (变换矩阵 T　＝[R t]) 的 李代数形式 f   李群形式为 exp(f)
     * si * [ui,vi,1] = K * T * Pi = K * exp(f) * Pi      这里 exp(f) * Pi  为 4*1维的需要为齐次表示 需要转换为 非齐次表示
     * 重投影误差  e =  sum( [ ci 1 ] - 1/si * K * exp(f) * Pi )^2  ；   K * exp(f) * Pi 为三维点的重投影坐标
     * 最小化重投影误差 得到 变换矩阵李代数形式 f  
     * 由于  [ ci 1 ] 最后一个为1  误差约束e 为两个方程  而 f  为6个自由度  x1 x2 x3 x4 x5 x6
     * 最小二乘优化 用于最小化一个函数   e(x + ∇x) = e(x)  +  J * ∇x
     * 所以 雅克比矩阵 J 为 2*6的矩阵
     * 
     * 雅克比J的推导：
     * si * [ ci 1 ] = K * T * Pi = K * exp(f) * Pi  = K * Pi'   Pi'为相机坐标系下的坐标  exp(f) * Pi  前三维 (Xi', Yi', Zi') 
     *  s*u       [fx 0 cx       X'
     *  s*v  =     0 fy cy  *    Y'
     *   s         0 0  1]       Z'
     *  利用第三行消去s(实际上就是 P'的深度) 
     *  u = fx * X'/Z' + cx
     *  v = fy * Y'/Z'  + cy 
     * 
     * [1]
     *  我们对 变换矩阵 T的 李代数形式 f 左乘 扰动量 ∇f
     e = [ ci 1 ] - 1/si * K * exp(f) * Pi 　＝　[ ci 1 ] - 1/si * K *　Pi'
     *  误差e 对∇f的偏导数 =  e 对P'的偏导数 *  P'对∇f的偏导数
     * 
     * e 对P'的偏导数 = - [ u对X'的偏导数 u对Y'的偏导数 u对Z'的偏导数;
     *                     v对X'的偏导数 v对Y'的偏导数  v对Z'的偏导数]  = - [ fx/Z'   0        -fx * X'/Z' ^2 
     *                                                                      0       fy/Z'    -fy* Y'/Z' ^2]
     *  P'对∇f的偏导数 = [ I  -P'叉乘矩阵]  3*6大小   平移在前  旋转在后
     *  = [ 1 0  0   0   Z'   -Y' 
     *      0 1  0  -Z'  0    X'
     *      0 0  1   Y'  -X   0]
     * 有向量 t = [ a1 a2 a3] 其
     * 叉乘矩阵 = [0  -a3  a2;
     *            a3  0  -a1; 
     *           -a2  a1  0 ]  
     * 
     * 两者相乘得到  平移在前 旋转在后
     * J = - [fx/Z'   0      -fx * X'/Z'^2   -fx * X'*Y'/Z' ^2      fx + fx * X'^2/Z'^2    -fx*Y'/Z'
     *         0     fy/Z'   -fy* Y'/Z'^2    -fy -fy* Y'^2/Z'^2     fy * X'*Y'/Z'^2        fy*X'/Z'    ] 
     * 如果是 旋转在前 平移在后 调换前三列  后三列 
     // 旋转在前 平移在后   g2o 
     * J =  [ fx *X'*Y'/Z'^2       -fx *(1 + X'^2/Z'^2)   fx*Y'/Z'  -fx/Z'   0       fx * X'/Z'^2 
     *        fy *(1 + Y'^2/Z'^2)  -fy * X'*Y'/Z'^2       -fy*X'/Z'   0     -fy/Z'   fy* Y'/Z'^2     ] 

     * [2] 优化变量为3D点坐标时Pi   
      e = [ ci 1 ] - 1/si * K * exp(f) * Pi = [ ci 1 ] - 1/si * K *　Pi'
     * e 对Pi的偏导数   = e 对Pi'的偏导数 *  Pi'对Pi的偏导数 = e 对P'的偏导数 * R
     * P' = R * P + t
     * P'对P的偏导数  = R

     J = e 对P'的偏导数  * R
       = - [ fx/Z'   0        -fx * X'/Z' ^2  *  R
              0       fy/Z'    -fy* Y'/Z' ^2]

3. 3D-3D　非线性最小二乘优化
    * ei = Pi - exp(f) * Pi'  = P - P‘ 李代数形式 的 变换矩阵 对误差求导 得到 迭代优化 梯度
    * 误差有三维，而优化变量R,t，对应的李代数有６个变量
    * 所有误差对变量的偏导数雅克比矩阵 维度为　3×6 误差  对应的导数来优化变量，更新的增量
    * e 对 ∇f的导数  = P'对∇f的偏导数
    *  P'对∇f的偏导数 = [ I  -P'叉乘矩阵] 3*6大小   平移在前  旋转在后
    *  = [ 1 0  0  0   Z'   -Y' 
    *      0 1  0  -Z' 0    X'
    *      0 0  1  Y' -X   0]
    * 旋转在前  平移在后
    *  = [   0   Z'  -Y' 1 0  0 
    *        -Z' 0    X' 0 1  0 
    *        Y'  -X   0  0 0  1]
    * 
    * J = - P'对∇f的偏导数
    *  = [   0   -Z'   Y'  -1  0  0 
    *        Z'   0    -X'  0 -1  0 
    *        -Y'  X’    0   0  0 -1]