MATLAB结构模态分析
概述
在结构设计中,模态分析是结构动力学分析最重要的内容之一,也是考察结构抗风、抗震以及其他动载作用下结构稳定性必不可少的步骤。市面上,ANSYS、迈达斯、SAP等商业有限元软件可以完成结构的模态分析,但对设计者来说自编程序来实现依然很有意义。自编程序意义如下:1. 可以和商业软件互相作校核;2. 能从原理上更深入理解,避免看到一个计算结果没有概念,不知道对错。
模态分析的核心是求出结构的总刚度矩阵和总质量矩阵,并作特征值分析,求出结构的频率和振型。前处理包括数据的准备,后处理为画振型图,方便查看。
原理
模态分析的原理和一般有限元分析类型,即结构离散、计算单刚、生成总刚、支座处理,质量矩阵的生成和刚度矩阵类似。刚度矩阵和质量矩阵出来再作特征值分析,得到频率和振型。
以梁式桥为例,单元刚度矩阵采用铁木辛柯单元:

质量矩阵:

如果存在集中质量块的,集中质量块的质量矩阵:

单元之间组合时,采用同一个整体坐标系,单元局部坐标系转换到整体坐标系时,坐标转换矩阵为:
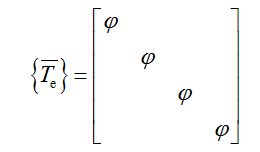
其中

单刚和单元质量矩阵坐标转换公式如下:
![]()
![]()
集中质量块不涉及坐标转换。
单刚和单元质量矩阵按节点分块,并累加到总刚对应位置中,如下图:
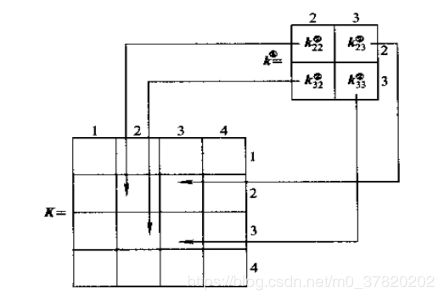
支座处理采用划零置一法:如果位移矩阵中第j行被约束,位移为Cj,则总刚总第j行和第j列都赋值0,第j行第j列元素赋值为1,如下图。
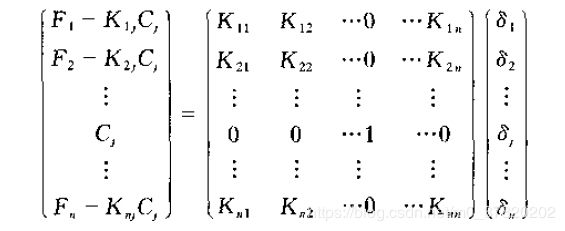
如果单元与单元之间存在刚臂,则设置一个虚拟的刚臂单元,刚臂单元质量为零,弹模和剪模放大10^10倍。
结构自由振动,忽略阻尼时,动力学方程如下:
![]()
即
![]()
其中,⍵j为第j阶频率,Xj为j阶振型。上面的方程特征值求解,则有:
![]()
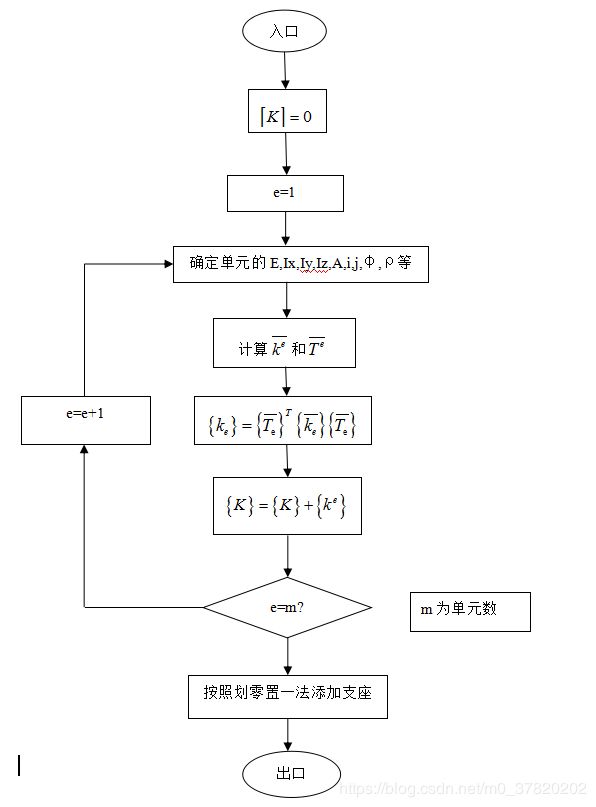
生成总刚流程图如下,总质量矩阵生成流程也类似:
代码实现
首先编写生成总刚和总质量矩阵的函数,保存为Timoshenko.m
function [Kzonggang,me,ke,ke1,Mzongzhiliang,Tzhuanhuan]=Timoshenko(danyuan,jiedian,jiemian,cailiao,gangbi,jizhongkuai)
%%%%Timoshenko 铁木辛柯单元算总刚度矩阵和总质量矩阵
% dangyuan 单元; jiedian 节点;jiemian 截面;cailiao 材料;gangbi 刚臂;jizhongkuai 集中质量块
% Kzonggang 总刚度矩阵;Mzongzhiliang 总质量矩阵;Tzhuanhuan 转换矩阵;me 单元质量矩阵集;ke 单元刚度矩阵集;ke1 坐标转换后的单元刚度矩阵集
c1=size(danyuan);
c2=size(jiedian);
c3=size(gangbi);
c4=size(jizhongkuai);
lenth=zeros(c1(1),1);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%杆件长度
aaa=zeros(c1(1),1);
Ay=zeros(c1(1),1);
Az=zeros(c1(1),1);
Iz=zeros(c1(1),1);
Iy=zeros(c1(1),1);
J=zeros(c1(1),1);
ry=zeros(c1(1),1);
rz=zeros(c1(1),1);
e=zeros(c1(1),1);
G=zeros(c1(1),1);
By=zeros(c1(1),1);
Bz=zeros(c1(1),1);
rrou=zeros(c1(1),1);%密度
ke=zeros(12,12,c1(1));
ke1=zeros(12,12,c1(1));
me=zeros(12,12,c1(1));
Mzongzhiliang=zeros(6*c2(1));
Kzonggang=zeros(6*c2(1));
kee=zeros(12,12);
Tzhuanhuan=zeros(12,12,c1(1));%转换矩阵
fai=zeros(3,3,c1(1));%%%%%%%%%%%%%%%%%%%%%%%%%%%%单元转换矩阵
ll=zeros(3);
lll=zeros(12);
for i=1:c1(1);
a=danyuan(i,1);
b=danyuan(i,2);
a0=jiedian(a,4);
b0=jiedian(b,4);
a1=(jiedian(b,1)-jiedian(a,1));
a2=(jiedian(b,2)-jiedian(a,2));
a3=(jiedian(b,3)-jiedian(a,3));
lenth(i)=sqrt(a1*a1+a2*a2+a3*a3);%杆件长度
%%%%%%
fai(1,1,i)=a1/lenth(i);
fai(1,2,i)=a2/lenth(i);
fai(1,3,i)=a3/lenth(i);
alfa=fai(1,1,i);
beita=danyuan(i,4);
x0=[1 0 0];
y0=[0 1 0];
z0=[0 0 1];
x1=[fai(1,1,i) fai(1,2,i) fai(1,3,i)];
if(alfa~=1)
T0=cross(x0,x1);
T=T0/norm(T0,2);
dy1=cross(T,y0);
if(norm(dy1)==0)
y1=y0;
else
dy1=dy1/norm(dy1);
dy2=cross(dy1,T);
dy2=dy2/norm(dy2);
if(T(1)==dy2(1))
s1=y0(2:3);
s2=[T(2:3);dy2(2:3)];
elseif(T(2)==dy2(2))
s1=y0(1:3:2);
s2=[T(1:3:2);dy2(1:3:2)];
else
s1=y0(2:3);
s2=[T(2:3);dy2(2:3)];
end
ay=s1/s2;
dy3=cos(alfa)*dy2+sin(alfa)*dy1;
y1=ay*[T;dy3];
end
z1=cross(x1,y1);
else
y1=y0;
z1=z0;
end
fai(2,:,i)=[cos(beita) sin(beita)]*[y1;z1];
fai(3,:,i)=[-sin(beita) cos(beita)]*[y1;z1];%转换矩阵
%%%%%%%
Ay(i)=(jiemian(a0,2)+jiemian(b0,2))/2;
Az(i)=(jiemian(a0,3)+jiemian(b0,3))/2;
aaa(i)=(jiemian(a0,1)+jiemian(b0,1))/2;
Iz(i)=(jiemian(a0,6)+jiemian(b0,6))/2;
Iy(i)=(jiemian(a0,5)+jiemian(b0,5))/2;
J(i)=(jiemian(a0,4)+jiemian(b0,4))/2;
ry(i)=sqrt(Iy(i)/aaa(i));
rz(i)=sqrt(Iz(i)/aaa(i));
%ry(i)=0;
%rz(i)=0;
a0=danyuan(i,3);
e(i)=cailiao(a0,1);%弹模
G(i)=cailiao(a0,2);%剪模
rrou(i)=cailiao(a0,3);
ll(:,:)=fai(:,:,i);
end
if(c3(2)>1) %刚性单元刚度异常大,密度为0
for i=1:c3(2)-1
a0=gangbi(i+1);
rrou(a0)=0;
e(a0)=10000000000000000000;
G(a0)=10000000000000000000;
end
end
for i=1:c1(1);
By(i)=12*e(i)*Iz(i)/(G(i)*Ay(i)*lenth(i)*lenth(i));
Bz(i)=12*e(i)*Iy(i)/(G(i)*Az(i)*lenth(i)*lenth(i));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%求单元长度及转换矩阵
for j=1:c1(1)
t=zeros(12);
ke(1,1,j)=e(j)*aaa(j)/lenth(j);
ke(7,1,j)=-e(j)*aaa(j)/lenth(j);
ke(2,2,j)=G(j)*Ay(j)/lenth(j);
ke(6,2,j)=0.5*G(j)*Ay(j);
ke(8,2,j)=-G(j)*Ay(j)/lenth(j);
ke(12,2,j)=0.5*G(j)*Ay(j);
ke(3,3,j)=G(j)*Az(j)/lenth(j);
ke(5,3,j)=-0.5*G(j)*Az(j);
ke(9,3,j)=-G(j)*Az(j)/lenth(j);
ke(11,3,j)=-0.5*G(j)*Az(j);
ke(4,4,j)=G(j)*J(j)/lenth(j);
ke(10,4,j)=-G(j)*J(j)/lenth(j);
ke(5,5,j)=0.25*G(j)*Az(j)*lenth(j)+e(j)*Iy(j)/lenth(j);
ke(9,5,j)=0.5*G(j)*Az(j);
ke(11,5,j)=0.25*G(j)*Az(j)*lenth(j)-e(j)*Iy(j)/lenth(j);
ke(6,6,j)=0.25*G(j)*Ay(j)*lenth(j)+e(j)*Iz(j)/lenth(j);
ke(8,6,j)=-0.5*G(j)*Ay(j);
ke(12,6,j)=0.25*G(j)*Ay(j)*lenth(j)-e(j)*Iz(j)/lenth(j);
ke(7,7,j)=e(j)*aaa(j)/lenth(j);
ke(8,8,j)=G(j)*Ay(j)/lenth(j);
ke(12,8,j)=-0.5*G(j)*Ay(j);
ke(9,9,j)=G(j)*Az(j)/lenth(j);
ke(11,9,j)=0.5*G(j)*Az(j);
ke(10,10,j)=G(j)*J(j)/lenth(j);
ke(11,11,j)=0.25*G(j)*Az(j)*lenth(j)+e(j)*Iy(j)/lenth(j);
ke(12,12,j)=0.25*G(j)*Ay(j)*lenth(j)+e(j)*Iz(j)/lenth(j);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
me(1,1,j)=2*aaa(j);
me(7,1,j)=aaa(j);
me(2,2,j)=2*aaa(j);
me(8,2,j)=aaa(j);
me(3,3,j)=2*aaa(j);
me(9,3,j)=aaa(j);
me(4,4,j)=2*J(j);
me(10,4,j)=J(j);
me(5,5,j)=2/35*aaa(j)*lenth(j);
me(11,5,j)=-3/70*aaa(j)*lenth(j);
me(6,6,j)=2/35*aaa(j)*lenth(j);
me(12,6,j)=-3/70*aaa(j)*lenth(j);
me(7,7,j)=2*aaa(j);
me(8,8,j)=2*aaa(j);
me(9,9,j)=2*aaa(j);
me(10,10,j)=2*J(j);
me(11,11,j)=2/35*aaa(j)*lenth(j);
me(12,12,j)=2/35*aaa(j)*lenth(j);
for k1=1:11
for k2=k1+1:12
ke(k1,k2,j)=ke(k2,k1,j);
me(k1,k2,j)=me(k2,k1,j);
end
end
me(:,:,j)=(rrou(j)*lenth(j))*me(:,:,j)/6;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%输入局部坐标下单刚及一致质量矩阵
for k1=1:3
for k2=1:3
t(k1,k2)=fai(k1,k2,j);
t(k1+3,k2+3)=fai(k1,k2,j);
t(k1+6,k2+6)=fai(k1,k2,j);
t(k1+9,k2+9)=fai(k1,k2,j);
end
end
Tzhuanhuan(:,:,j)=t;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%输入转换矩阵
kee(:,:)=ke(:,:,j);
kee=t'*kee*t;%%%%%%%%%%%%%%%%%%%%%%%整体坐标下单刚
ke1(:,:,j)=kee;
lll(:,:)=me(:,:,j);
lll=t'*lll*t;
a=danyuan(j,1)-1;
b=danyuan(j,2)-1;
for k1=1:6
for k2=1:6
Kzonggang(6*a+k1,6*a+k2)= Kzonggang(6*a+k1,6*a+k2)+kee(k1,k2);
Kzonggang(6*a+k1,6*b+k2)= Kzonggang(6*a+k1,6*b+k2)+kee(k1,k2+6);
Kzonggang(6*b+k1,6*a+k2)= Kzonggang(6*b+k1,6*a+k2)+kee(k1+6,k2);
Kzonggang(6*b+k1,6*b+k2)= Kzonggang(6*b+k1,6*b+k2)+kee(k1+6,k2+6);
%%%%
Mzongzhiliang(6*a+k1,6*a+k2)= Mzongzhiliang(6*a+k1,6*a+k2)+lll(k1,k2);
Mzongzhiliang(6*a+k1,6*b+k2)= Mzongzhiliang(6*a+k1,6*b+k2)+lll(k1,k2+6);
Mzongzhiliang(6*b+k1,6*a+k2)= Mzongzhiliang(6*b+k1,6*a+k2)+lll(k1+6,k2);
Mzongzhiliang(6*b+k1,6*b+k2)= Mzongzhiliang(6*b+k1,6*b+k2)+lll(k1+6,k2+6);
end
end
end
if(c4(1)>1)
for i=1:c4(1)-1
a0=jizhongkuai(i+1,1);
b0=jizhongkuai(i+1,2);
Mzongzhiliang(6*a0-5,6*a0-5)=Mzongzhiliang(6*a0-5,6*a0-5)+b0;
Mzongzhiliang(6*a0-4,6*a0-4)=Mzongzhiliang(6*a0-4,6*a0-4)+b0;
Mzongzhiliang(6*a0-3,6*a0-3)=Mzongzhiliang(6*a0-3,6*a0-3)+b0;
end
end
接下来编写绘图的方法,保存为draw.m
function picture=draw(jiedian,danyuan,tzxlsjzg,index)
warning off;
c1=size(jiedian);
c2=size(danyuan);
Ndy=c2(1);
NN=c1(1);
ss=2/max(abs(tzxlsjzg(:,index)));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%变形前
plot3(jiedian(:,1),jiedian(:,2),jiedian(:,3),'.r')%画节点
hold on
for j=1:Ndy
a1=danyuan(j,1);
a2=danyuan(j,2);
Xdx=[jiedian(a1,1);jiedian(a2,1)];
Xdy=[jiedian(a1,2);jiedian(a2,2)];
Xdz=[jiedian(a1,3);jiedian(a2,3)];
plot3(Xdx,Xdy,Xdz,'-r')%画单元
hold on
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%变形前
%%%%%%%%%%%%%%%%%%%%%%%%%%%%变形后
ZXjiedian=zeros(NN,3);
for j=1:NN
ZXjiedian(j,1)=jiedian(j,1)+ss*tzxlsjzg(6*j-5,index);
ZXjiedian(j,2)=jiedian(j,2)+ss*tzxlsjzg(6*j-4,index);
ZXjiedian(j,3)=jiedian(j,3)+ss*tzxlsjzg(6*j-3,index);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
plot3(ZXjiedian(:,1),ZXjiedian(:,2),ZXjiedian(:,3),'*b');%画节点
hold on
for j=1:Ndy
a1=danyuan(j,1);
a2=danyuan(j,2);
Xdx=[ZXjiedian(a1,1);ZXjiedian(a2,1)];
Xdy=[ZXjiedian(a1,2);ZXjiedian(a2,2)];
Xdz=[ZXjiedian(a1,3);ZXjiedian(a2,3)];
plot3(Xdx,Xdy,Xdz,'-b')%画单元
hold on
end
axis equal
grid on
hold off
fp=strcat('第',int2str(index),'阶振型图');
title(fp);
接下来编写主程序
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%数据读取
a10='G:\模态分析';
a11='最新数据1.txt';
a1=strcat(a10,'\',a11);
fid1=fopen(a1,'r');
shuju=fscanf(fid1,'%f %f',[9,1]);
NN=fscanf(fid1,'%f %f',[1,1]); %节点总数
jiedian=fscanf(fid1,'%f %f',[5,NN]); %节点信息
jiedian=jiedian';
Nzljd=fscanf(fid1,'%f %f',[1,1]); %主梁节点数
Nqiaodun=fscanf(fid1,'%f %f',[1,1]); %桥墩数
Ngdjds=fscanf(fid1,'%f %f',[Nqiaodun,1]); %各墩节点数
Hgddm=fscanf(fid1,'%f %f',[Nqiaodun,1]); %各墩墩地面处竖坐标
Ndy=fscanf(fid1,'%f %f',[1,1]); %单元数
danyuan=fscanf(fid1,'%f %f',[4,Ndy]); %单元信息
danyuan=danyuan';
Nldjiedian=fscanf(fid1,'%f %f',[1,1]); %刚臂单元数
ldjedangyuan=fscanf(fid1,'%f %f',[Nldjiedian,1]); %刚臂单元号
ldjedangyuan=ldjedangyuan';
Nzhizuo=fscanf(fid1,'%f %f',[1,1]); %支座数
zhizuo=fscanf(fid1,'%f %f',[3,Nzhizuo]); %支座信息
zhizuo=zhizuo';
%%%% %%%
Njiemian=fscanf(fid1,'%f %f',[1,1]); %截面数
jiemian=fscanf(fid1,'%f %f',[24,Njiemian]); %截面特性
jiemian=jiemian';
sflxs=fscanf(fid1,'%f %f',[12,Njiemian]); %三分力系数
sflxs=sflxs';
Ncailiao=fscanf(fid1,'%f %f',[1,1]); %材料数
cailiao=fscanf(fid1,'%f %f',[3,Ncailiao]); %材料特性E,G,rou
cailiao=cailiao';
Njzm=fscanf(fid1,'%f %f',[1,1]); %集中质量块数
if(Njzm>0)
jzm=fscanf(fid1,'%f %f',[2,Njzm]); %集中块节点号及质量
jzm=jzm';
end
fclose(fid1);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%总刚及质量矩阵
Nldjiedian=ldjedangyuan(1,1);
jiedian1=jiedian(:,1:4);
for i=1:NN
i1=jiedian(i,4);
h1=jiemian(i1,9);
if(jiedian(i,5)==0)
jiedian1(i,3)=jiedian(i,3)-h1;
end
end
[KK,me,Kke,Kke1,M,tt]=Timoshenko(danyuan,jiedian1,jiemian,cailiao,ldjedangyuan,jzm);
KK1=KK;
KK2=KK;
M1=M;
M2=M;
for i=1:Nzhizuo
k=6*(zhizuo(i,1)-1)+zhizuo(i,2);
KK1(k,:)=zeros(1,6*NN);
KK2(k,:)=zeros(1,6*NN);
M1(k,:)=zeros(1,6*NN);
M2(k,:)=zeros(1,6*NN);
KK1(:,k)=zeros(6*NN,1);
KK2(:,k)=zeros(6*NN,1);
M1(:,k)=zeros(6*NN,1);
M2(:,k)=zeros(6*NN,1);
KK1(k,k)=-1;
KK2(k,k)=1;
M1(k,k)=0.00001;
M2(k,k)=1;
end
[tzxlsjzg,tzzsjzg]=eig(KK1,M1);%%%%%%%特征向量-振型,特征值-频率平方
omiga=zeros(6*NN,1);
for i=1:6*NN
omiga(i)=tzzsjzg(i,i);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%对振型和频率排序
omiga11=omiga;
omiga21=omiga;
t=max(omiga21);
s=zeros(6*NN,1);
for i=1:6*NN
a=1;
for j=1:6*NN
if(omiga11(a)>omiga11(j))
a=j;
end
end
s(i)=a;
omiga11(a)=t+1;
end
tzxlsjzg2=tzxlsjzg;
for i=1:6*NN
a=s(i);
omiga(i)=omiga21(a);
tzxlsjzg(:,i)=tzxlsjzg2(:,a);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%支座处奇异值处理
omiga0=omiga;
omiga=omiga(Nzhizuo+1:Nzhizuo+10);
omiga=sqrt(omiga);
for i=1:Nzhizuo
k=6*(zhizuo(i,1)-1)+zhizuo(i,2);
tzxlsjzg(k,:)=zeros(1,6*NN);
end
tzxlsjzg1=tzxlsjzg(:,Nzhizuo+1:6*NN);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
draw(jiedian,dangyuan,tzxlsjzg1,1)%%第一阶振型图,调整最后一个实参可以得到其他阶振型。
结果
输入文件为"最新数据1.txt",路径要与主程序中的路径匹配,内容如下
31.3 0.05 1024 11.6 8 21 6.28318 15 5
71
0 0 0 20 0
4 0 0 19 0
8 0 0 18 0
12 0 0 17 0
16 0 0 16 0
20 0 0 15 0
24 0 0 14 0
28 0 0 13 0
32 0 0 12 0
36 0 0 11 0
40 0 0 10 0
43.5 0 0 9 0
47 0 0 8 0
50.5 0 0 7 0
54 0 0 6 0
57.5 0 0 5 0
61 0 0 4 0
64.5 0 0 3 0
65.5 0 0 2 0
68 0 0 1 0
69 0 0 1 0
70 0 0 1 0
72 0 0 1 0
74 0 0 1 0
75 0 0 1 0
76 0 0 1 0
78.5 0 0 2 0
79.5 0 0 3 0
83 0 0 4 0
86.5 0 0 5 0
90 0 0 6 0
93.5 0 0 7 0
97 0 0 8 0
100.5 0 0 9 0
104 0 0 10 0
108 0 0 11 0
112 0 0 12 0
116 0 0 13 0
120 0 0 14 0
124 0 0 15 0
128 0 0 16 0
132 0 0 17 0
136 0 0 18 0
140 0 0 19 0
144 0 0 20 0
69 0 -8.8 21 1
69 0 -11.8 21 1
69 0 -14.8 21 1
69 0 -17.8 21 1
69 0 -21.8 21 1
69 0 -25.8 21 1
69 0 -27.8 21 1
69 0 -29.8 21 1
69 0 -31.8 21 1
69 0 -33.8 21 1
69 0 -37.8 21 1
75 0 -8.8 23 2
75 0 -11.8 23 2
75 0 -14.8 23 2
75 0 -17.8 23 2
75 0 -21.8 23 2
75 0 -25.8 23 2
75 0 -27.8 23 2
75 0 -29.8 23 2
75 0 -31.8 23 2
75 0 -33.8 23 2
75 0 -37.8 23 2
70 0 -17.8 22 -1
74 0 -17.8 22 -1
70 0 -27.8 22 -1
74 0 -27.8 22 -1
45
2
11 11
-29.8 -29.8
72
1 2 1 0
2 3 1 0
3 4 1 0
4 5 1 0
5 6 1 0
6 7 1 0
7 8 1 0
8 9 1 0
9 10 1 0
10 11 1 0
11 12 1 0
12 13 1 0
13 14 1 0
14 15 1 0
15 16 1 0
16 17 1 0
17 18 1 0
18 19 1 0
19 20 1 0
20 21 1 0
21 22 1 0
22 23 1 0
23 24 1 0
24 25 1 0
25 26 1 0
26 27 1 0
27 28 1 0
28 29 1 0
29 30 1 0
30 31 1 0
31 32 1 0
32 33 1 0
33 34 1 0
34 35 1 0
35 36 1 0
36 37 1 0
37 38 1 0
38 39 1 0
39 40 1 0
40 41 1 0
41 42 1 0
42 43 1 0
43 44 1 0
44 45 1 0
46 47 1 0
47 48 1 0
48 49 1 0
49 50 1 0
50 51 1 0
51 52 1 0
52 53 1 0
53 54 1 0
54 55 1 0
55 56 1 0
57 58 1 0
58 59 1 0
59 60 1 0
60 61 1 0
61 62 1 0
62 63 1 0
63 64 1 0
64 65 1 0
65 66 1 0
66 67 1 0
49 68 1 0
68 69 1 0
69 60 1 0
52 70 1 0
70 71 1 0
71 63 1 0
21 46 1 0
25 57 1 0
6
65 67 68 70 71 72
12
56 1 0
56 2 0
56 3 0
56 4 0
56 5 0
56 6 0
67 1 0
67 2 0
67 3 0
67 4 0
67 5 0
67 6 0
23
38.725 15.295 22.389 404.427 343.054 252.508 5.800 5.800 4.465 4.335 17.304 17.113 39.831 19.866 5.800 4.335 -5.800 4.465 5.800 4.465 3.500 -4.335 -3.500 -4.335
28.405 10.158 15.577 315.093 279.262 215.197 5.800 5.800 4.517 4.283 20.205 22.678 39.831 22.777 5.800 4.283 -5.800 4.517 5.800 4.517 3.500 -4.283 -3.500 -4.283
28.028 10.116 15.31 306.713 267.434 212.508 5.8 5.8 4.436 4.228 19.647 22.68 39.559 22.547 5.8 4.228 -5.8 4.436 5.8 4.436 3.5 -4.228 -3.5 -4.228
26.75 9.96 14.423 278.857 229.828 203.419 5.8 5.8 4.162 4.043 17.812 22.7 38.641 21.773 5.8 4.043 -5.8 4.162 5.8 4.162 3.5 -4.043 -3.5 -4.043
25.555 9.803 13.584 253.223 197.825 194.91 5.8 5.8 3.907 3.868 16.169 22.715 37.781 21.047 5.8 3.868 -5.8 3.907 5.8 3.907 3.5 -3.868 -3.5 -3.868
24.439 9.638 12.797 229.612 170.559 186.943 5.8 5.8 3.669 3.703 14.697 22.719 36.975 20.365 5.8 3.703 -5.8 3.669 5.8 3.669 3.5 -3.703 -3.5 -3.703
23.397 9.462 12.056 208.058 147.369 179.508 5.8 5.8 3.448 3.548 13.38 22.726 36.223 19.729 5.8 3.548 -5.8 3.448 5.8 3.448 3.5 -3.548 -3.5 -3.548
19.79 9.099 8.709 173.62 121.611 155.516 5.8 5.8 3.251 3.397 15.115 20.098 35.527 20.141 5.8 3.397 -5.8 3.251 5.8 3.251 3.5 -3.397 -3.5 -3.397
19.035 8.894 8.218 157.754 105.993 150.112 5.8 5.8 3.057 3.271 13.848 20.152 34.887 19.601 5.8 3.271 -5.8 3.057 5.8 3.057 3.5 -3.271 -3.5 -3.271
18.348 8.725 7.764 143.753 92.858 145.176 5.8 5.8 2.882 3.153 12.732 20.195 34.301 19.105 5.8 3.153 -5.8 2.882 5.8 2.882 3.5 -3.153 -3.5 -3.153
17.637 8.56 7.335 130.125 80.4 140.079 5.8 5.8 2.702 3.031 11.618 20.251 33.697 18.595 5.8 3.031 -5.8 2.702 5.8 2.702 3.5 -3.031 -3.5 -3.031
17.012 8.4 6.933 118.169 70.334 135.595 5.8 5.8 2.544 2.923 10.673 20.299 33.165 18.145 5.8 2.923 -5.8 2.544 5.8 2.544 3.5 -2.923 -3.5 -2.923
16.475 8.246 6.571 107.939 62.296 131.725 5.8 5.8 2.41 2.827 9.884 20.337 32.705 17.755 5.8 2.827 -5.8 2.41 5.8 2.41 3.5 -2.827 -3.5 -2.827
16.017 8.113 6.288 99.609 55.935 128.439 5.8 5.8 2.296 2.746 9.232 20.376 32.315 17.425 5.8 2.746 -5.8 2.296 5.8 2.296 3.5 -2.746 -3.5 -2.746
13.752 7.856 4.236 83.764 48.674 111.326 5.8 5.8 2.171 2.712 12.139 17.787 31.997 18.155 5.8 2.712 -5.8 2.171 5.8 2.171 3.5 -2.712 -3.5 -2.712
13.508 7.763 4.108 79.388 45.197 109.654 5.8 5.8 2.097 2.662 11.581 17.853 31.749 17.947 5.8 2.662 -5.8 2.097 5.8 2.097 3.5 -2.662 -3.5 -2.662
13.342 7.701 4.019 76.364 42.852 108.488 5.8 5.8 2.046 2.626 11.2 17.885 31.573 17.797 5.8 2.626 -5.8 2.046 5.8 2.046 3.5 -2.626 -3.5 -2.626
13.241 7.663 3.965 74.548 41.472 107.783 5.8 5.8 2.015 2.604 10.971 17.907 31.467 17.707 5.8 2.604 -5.8 2.015 5.8 2.015 3.5 -2.604 -3.5 -2.604
13.205 7.653 3.946 73.963 41.002 107.539 5.8 5.8 2.004 2.596 10.891 17.919 31.431 17.677 5.8 2.596 -5.8 2.004 5.8 2.004 3.5 -2.596 -3.5 -2.596
13.205 7.653 3.946 73.963 41.002 107.539 5.8 5.8 2.004 2.596 10.891 17.919 31.431 17.677 5.8 2.596 -5.8 2.004 5.8 2.004 3.5 -2.596 -3.5 -2.596
16.000 13.333 13.333 17.974 5.333 85.333 4.000 4.000 1.000 1.000 0.500 8.000 20.000 0.000 4.000 1.000 -4.000 1.000 4.000 1.000 4.000 -1.000 -4.000 -1.000
4.800 4.000 4.000 0.938 0.256 14.400 3.000 3.000 0.400 0.400 0.080 4.500 13.600 0.000 3.000 0.400 -3.000 0.400 3.000 0.400 3.000 -0.400 -3.000 -0.400
16.000 13.333 13.333 17.974 5.333 85.333 4.000 4.000 1.000 1.000 0.500 8.000 20.000 0.000 4.000 1.000 -4.000 1.000 4.000 1.000 4.000 -1.000 -4.000 -1.000
2.174 -0.431 -0.334 2.253 -0.534 -0.330 2.327 -0.628 -0.324 -2.188 2.824 -0.141
2.174 -0.431 -0.334 2.253 -0.534 -0.330 2.327 -0.628 -0.324 -2.188 2.824 -0.141
2.174 -0.431 -0.334 2.253 -0.534 -0.330 2.327 -0.628 -0.324 -2.188 2.824 -0.141
2.028 -0.384 -0.311 2.101 -0.479 -0.304 2.174 -0.582 -0.298 -2.083 2.833 -0.185
1.921 -0.397 -0.295 1.986 -0.496 -0.287 2.045 -0.591 -0.279 -1.772 2.780 -0.227
1.802 -0.381 -0.286 1.864 -0.473 -0.273 1.915 -0.583 -0.264 -1.614 2.893 -0.320
1.700 -0.393 -0.277 1.754 -0.502 -0.266 1.801 -0.595 -0.258 -1.449 2.899 -0.276
1.612 -0.393 -0.262 1.661 -0.492 -0.251 1.710 -0.595 -0.239 -1.404 2.892 -0.334
1.538 -0.390 -0.265 1.586 -0.494 -0.251 1.633 -0.601 -0.239 -1.365 3.014 -0.365
1.437 -0.404 -0.252 1.480 -0.511 -0.239 1.521 -0.613 -0.225 -1.210 2.996 -0.395
1.394 -0.410 -0.240 1.434 -0.514 -0.226 1.475 -0.610 -0.212 -1.160 2.867 -0.402
1.339 -0.392 -0.232 1.375 -0.496 -0.218 1.410 -0.592 -0.204 -1.013 2.866 -0.411
1.288 -0.371 -0.235 1.322 -0.473 -0.220 1.357 -0.568 -0.205 -0.986 2.826 -0.425
1.231 -0.367 -0.242 1.262 -0.468 -0.228 1.297 -0.571 -0.214 -0.945 2.918 -0.407
1.217 -0.370 -0.228 1.250 -0.472 -0.213 1.283 -0.569 -0.197 -0.958 2.856 -0.441
1.192 -0.355 -0.230 1.226 -0.459 -0.213 1.261 -0.560 -0.198 -0.986 2.928 -0.459
1.177 -0.378 -0.228 1.209 -0.480 -0.212 1.239 -0.573 -0.196 -0.891 2.807 -0.457
1.164 -0.377 -0.225 1.195 -0.479 -0.208 1.224 -0.573 -0.192 -0.858 2.816 -0.467
1.108 -0.401 -0.226 1.131 -0.496 -0.211 1.160 -0.594 -0.195 -0.752 2.769 -0.449
1.108 -0.401 -0.226 1.131 -0.496 -0.211 1.160 -0.594 -0.195 -0.752 2.769 -0.449
0.245 -0.016 0.252 0.257 0.111 0.208 0.266 0.168 0.166 0.309 2.639 -1.232
0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
0.261 -0.147 0.038 0.254 -0.074 -0.007 0.239 0.064 -0.058 -0.313 3.027 -1.375
1
36000000000 15430000000 2650
2
21 90000
25 90000
运行结果如下图示:

还可以查看其他振型,以及频率。
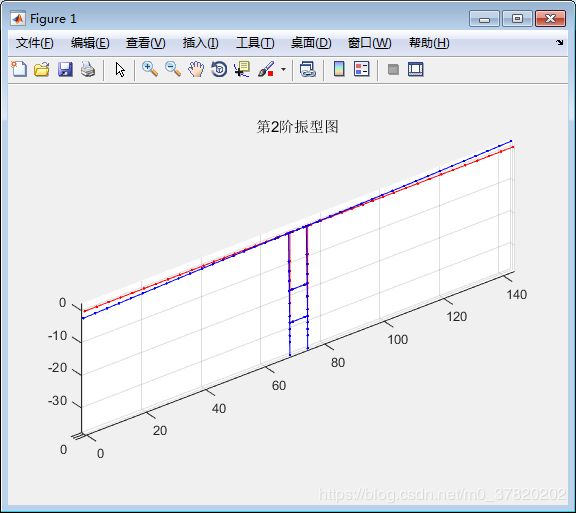
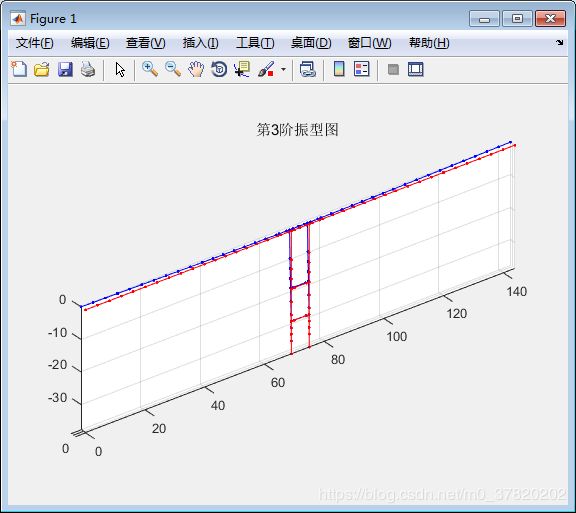
前十阶频率为:
1.98871609035383
4.42377330320088
6.14903626324008
8.79482569837443
9.72747024277138
14.7595719825660
28.5067851469935
31.1482902649112
36.3710508358691
54.6773606580982