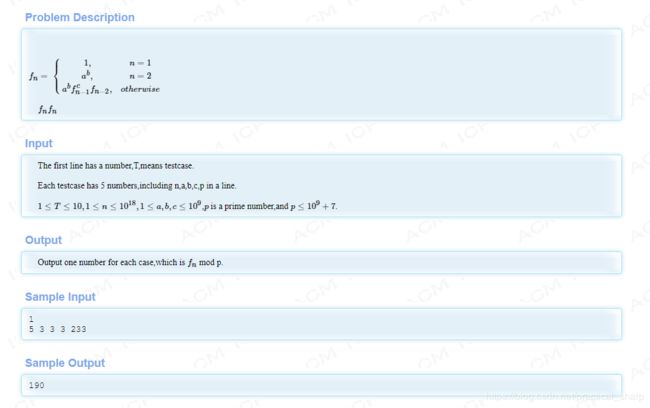
HDU5667 Sequence

首先附上题目链接

http://acm.hdu.edu.cn/showproblem.php?pid=5667

题目分析

像这种递推公式的问题，n很大的时候，常用的处理方法是矩阵快速幂，但是这个好像很难构造。

博主思路如下：取对数 设k(i) = loga(f(i))

那么 根据推导
k(1) = loga(1)=0
k(2) = loga(a^b) = b
k(i) = b + c*k(i-1)+k(i-2)
那么可以用矩阵快速幂的方式 求解 k(n) f(n) = a^k(n)再通过整数快速幂的方式求解。
还有一个问题：k(n)很大 直接求幂肯定连int64_t都要溢出 那么运用费马小定理

a^p-1=== 1 mod p

即是：a^p-1=== a⁰ mod p 所以循环节是p-1,我们可以通过对k(n)%(p-1)运算求得最小的余数

所以f(n) = a^(k(n)) = a^(k(n)%(p-1))%p
所以矩阵快速幂的取余算子也得到了

下面计算转移矩阵

设转移矩阵为T，初始矩阵为K
K ={ k(2), k(1), 1}^T={b,0,1}^T

那么转移矩阵T =

Matix T = {
	c,1,b,
	1,0,0,
	0,0,1
};

T*K的最右上角元素为k(3) 那么 T^(n-2)*K的最右上角元素为k(n)。

矩阵结构体

const int N = 3;
typedef struct Matix{
	int64_t m[N][N];
}Matix;

矩阵乘法

//矩阵乘法
Matix temp;
Matix Matix_Mutiply(Matix a,Matix b){
	memset(temp.m,0,sizeof(temp.m));//初始化矩阵temp
	for(int i=0;i<N;i++){
		for(int j=0;j<N;j++)
			for(int k=0;k<N;k++)
			temp.m[i][j] = (temp.m[i][j] + a.m[i][k]*b.m[k][j]%MOD)%MOD;//MOD = p-1 主函数中赋值
	}
	return temp;
}

矩阵快速幂

//矩阵快速幂
Matix C,d;//定义一个单位阵
Matix Matix_Pow(Matix a,int64_t n){
	memset(C.m,0,sizeof(C.m));d = a;//以免把a搞没了
	for(int i=0;i<N;i++) C.m[i][i] = 1;//单位阵定义出来了
	while(n){
		if(n & 1) C = Matix_Mutiply(C,d); //C = C*d;
		d = Matix_Mutiply(d,d);
		n = n>>1;
	}
	return C;
}

整数快速幂

//整数快速幂
int64_t fastpow(int64_t a,int64_t n){
	int64_t ans = 1,tp = a;
	if(n==0) return ans;
	while(n){
		if(n&1) ans = ans*tp%p;
		tp = tp*tp%p;
		n = n>>1;
	}
	return ans;
}

通过以上算法 求得 f(n) = a^(k(n)) = a^(k(n)%(p-1))%p

AC代码

//32802364	2020-03-18 00:52:56	Accepted	5667	31MS	1416K	1679 B	G++	sharpcoder
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int N = 3;//本题中所有方阵都是3维的
int64_t n,a,b,c,p;
int64_t MOD;//MOD = p-1;
typedef struct Matix{
	int64_t m[N][N];
}Matix;
//矩阵乘法
Matix temp;//全局变量可以减少空间复杂度
Matix Matix_Mutiply(Matix a,Matix b){
	memset(temp.m,0,sizeof(temp.m));//初始化矩阵temp
	for(int i=0;i<N;i++){
		for(int j=0;j<N;j++)
			for(int k=0;k<N;k++)
			temp.m[i][j] = (temp.m[i][j] + a.m[i][k]*b.m[k][j]%MOD)%MOD;
	}
	return temp;
}
//矩阵快速幂
Matix C,d;//定义一个单位阵
Matix Matix_Pow(Matix a,int64_t n){
	memset(C.m,0,sizeof(C.m));d = a;//以免把a搞没了
	for(int i=0;i<N;i++) C.m[i][i] = 1;//单位阵定义出来了
	while(n){
		if(n & 1) C = Matix_Mutiply(C,d); //C = C*d;
		d = Matix_Mutiply(d,d);
		n = n>>1;//右移 等价于n = n/2;
	}
	return C;
}
//整数快速幂
int64_t fastpow(int64_t a,int64_t n){
	int64_t ans = 1,tp = a;
	if(n==0) return ans;
	while(n){
		if(n&1) ans = ans*tp%p;
		tp = tp*tp%p;
		n = n>>1;
	}
	return ans;
}
int main(){
	int t;cin>>t;//一共有t组测试样例
	while(t--){
		cin>>n>>a>>b>>c>>p;//输入每组测试样例的n,a,b,c,p
		MOD = p-1;//不要忘记这一句了
		Matix K = {    //转移矩阵
			c,1,b,
			1,0,0,
			0,0,1
		};
		if(n==1){
			cout<<1<<endl;
			continue;
		}else if(n==2){
			cout<<fastpow(a,b)<<endl;
			continue;
		}
		//取对数之后 T(1) = loga 1 = 0;T(2) = loga a^b = b;
		Matix T = {   //初始矩阵
			b,0,0,
			0,0,0,
			1,0,0
		};
		K = Matix_Pow(K,n-2);//对转移矩阵求n-2次幂
		//T = Matix_Mutiply(K,T);
		//T(n) = K^(n-2)*T1
		T.m[0][0] = K.m[0][0]*b + K.m[0][1]*0 + K.m[0][2]*1;//T.m[0][0]即是上文中定义的k(n)
		cout<<fastpow(a,T.m[0][0])<<endl;
	}
	return 0;
}