数据结构之二叉搜索树

在前面的几章中，介绍了几种线性数据结构，主要包含数组、栈、队列、链表等。从本节开始，给大家介绍树这种数据结构。

在数据结构中，包括很多的树结构，像二叉树、二叉搜索树、线段树、字典树、红黑树等。本小节介绍的是二叉树和二叉搜索树，其余的树结构，会在后面的文章中再进行介绍。

树

在介绍二叉树之前，我们先准备些预备知识。

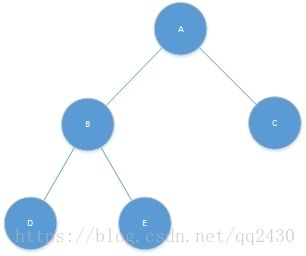
首先来看先什么是树。一颗树可以看做是由根节点（root）和以及0个或多个子树构成，如下图所示。

在树中，没有子节点的节点我们称之为叶子节点。具有相同父节点的节点我们称之为兄弟节点。对于任意节点n，从根节点到n节点的唯一路径的长我们称之为深度，所以根节点的深度为0。从任意节点n到一片叶子节点最长路径的长，我们称之为高度，所以所有叶子节点的高度都为0，一棵树的高度等于根节点的高度。

有了以上的定义，我们来分析下面的这颗树。在下面的这棵树中，根节点为A。B、C、D互为兄弟节点。B、E、F、H为叶子节点。B、C、D的深度为1，E、F、G节点的深度为2，H节点的深度为3。G的高度为1，D的高度为2，整棵树也就是根节点A的高度为3。

二叉树

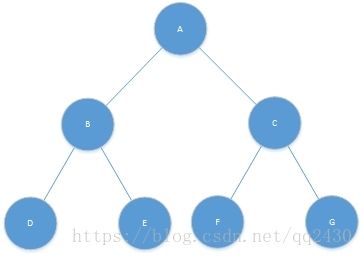
理解了上面树的定义后，理解二叉树就不简单很多。所谓的二叉树，就是每个节点置多有2个子节点的树，如下图所示，就是1颗二叉树。

满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。也可以这样理解，除叶子结点外的所有结点均有两个子结点，如下图所示。

完全二叉树

除了最后一层外，其余层所有节点数都达到最大，最后一层的节点都集中在左侧。如下图所示。

遍历方式

对于二叉树，有深度优先遍历和广度优先遍历，深度优先遍历也就是通常说的层次遍历。而广度优先遍历又分为前、中、后序遍历。

• 前序遍历：根节点->左子树->右子树
• 中序遍历：左子树->根节点->右子树
• 后序遍历：左子树->右子树->根节点
• 层序遍历：按照层次遍历即可

二叉搜索树

前面介绍了些预备知识，现在终于可以进入本节的正题了——二叉搜索树。

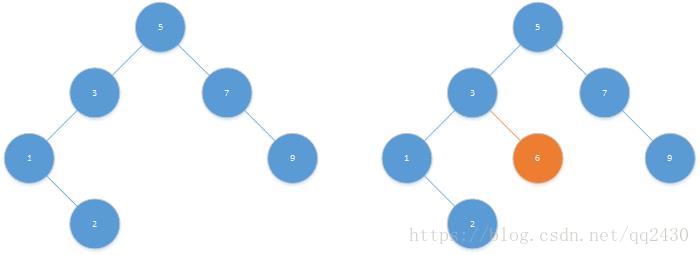
二叉搜索树又称为二叉查找树。它首先是一颗二叉树，当树中的每个节点N，其左子树所有节点的值都小于节点N的值，右子树节点的值都大于节点N的值。如下图中，左边的树是二叉搜索树，但右边不是，因为6大于5，但是却存在于5的左子树中。

下面我们用代码实现一颗二叉搜索树。

节点

二叉树中的节点可以分为3个部分，分别为指向左子树的指针，指向右子树的指针，以及节点存储的值。

public class BinarySearchTree<E extends Comparable> {

    private class Node {
        //左孩子节点
        private Node left;
        //右孩子节点
        private Node right;
        //节点值
        private E e;

        public Node() {
            this(null, null, null);
        }

        public Node(E e) {
            this(null, null, e);
        }

        public Node(Node left, Node right, E e) {
            this.left = left;
            this.right = right;
            this.e = e;
        }
    }

    //根节点
    private Node root;

    //树中元素的个数
    private int size;
}

查找元素

通过二叉搜索树的性质可以知道，对于任意一个节点x，它的左孩子节点值一定小于x的节点值，它的右孩子节点一定大于x的节点值。这样我们可以不断的通过递归比较节点值来进行查找。如果查找的值小于节点值，那么就在这个节点的左子树中进行递归查找。如果大于节点值，那么就在这个节点的右子树中进行递归查找，直到查找到某个节点值等于我们要查找的值，或者递归到底，说明树中不包含要查找的值。

   public boolean contains(E e) {
        if (e == null) {
            throw new IllegalArgumentException("element is null.");
        }
        return contains(root, e) != null;
    }

    private Node contains(Node node, E e) {
        if (node == null) {
            return null;
        }
        if (e.compareTo(node.e) < 0) {
            return contains(node.left, e);
        } else if (e.compareTo(node.e) > 0) {
            return contains(node.right, e);
        } else {
            return node;
        }
    }

添加元素

添加元素与查找元素类似，如果要添加的值小于节点值，那么在这个节点的左子树中添加元素。如果大于节点值，那么在这个节点的右子树中添加元素，如果等于节点值，说明树中已经包含这个元素，直接不进行处理即可。

 public void add(E e) {
        if (e == null) {
            throw new IllegalArgumentException("element is null.");
        }
        root = add(root, e);
    }

    private Node add(Node node, E e) {
        if (node == null) {
            size++;
            return new Node(e);
        }
        if (e.compareTo(node.e) < 0) {
            node.left = add(node.left, e);
        } else if (e.compareTo(node.e) > 0) {
            node.right = add(node.right, e);
        } else {
            //nothing to do
        }
        return node;
    }

删除元素

二叉搜索树删除一个元素相比于其他步骤比较复杂。要删除的节点会分为以下四种情况。

• 删除的节点是叶子节点：这种情况比较简单，直接将指向删除的节点的指针指向null即可。
• 删除的节点只有左子树：这种情况只需要将指向删除的节点的指针指向左子树即可。
• 删除的节点只有右子树：这种情况只需要将指向删除的节点的指针指向右子树即可。
• 删除的节点包含左右子树：这种情况较为复杂，通常的是选取右子树的最小值或者左子树的最大值作为为新的节点，替换到待删除节点的位置。如下图所示。

代码如下所示。

    public void remove(E e) {
        if (root == null) {
            throw new IllegalArgumentException("tree is empty.");
        }
        root = remove(root, e);
    }

    private Node remove(Node node, E e) {
        if (node == null) {
            throw new IllegalArgumentException("not contains: " + e);
        }
        if (e.compareTo(node.e) < 0) {
            node.left = remove(node.left, e);
            return node;
        } else if (e.compareTo(node.e) > 0) {
            node.right = remove(node.right, e);
            return node;
        } else {
            if (node.left != null && node.right != null) {
                //删除的节点有左右子树
                //选择右子树的最小值节点或者左子树的最大值节点作为替换要删除的节点。
                Node newNode = findMax(node.right);
                newNode.right = removeMin(node.right);
                newNode.left = node.left;
                //for gc
                node.left = node.right = null;
                return newNode;
            } else if (node.left != null) {
                //删除的节点只有左子树
                return node.left;
            } else if (node.right != null) {
                //删除的节点只有右子树
                return node.right;
            } else {
                //删除的是叶子节点
                return null;
            }
        }
    }

完整的二叉搜索树代码如下，简单实现了增删改查和前、中、后、层次遍历。

public class BinarySearchTree<E extends Comparable> {

    private class Node {
        //左孩子节点
        private Node left;
        //右孩子节点
        private Node right;
        //节点值
        private E e;

        public Node() {
            this(null, null, null);
        }

        public Node(E e) {
            this(null, null, e);
        }

        public Node(Node left, Node right, E e) {
            this.left = left;
            this.right = right;
            this.e = e;
        }
    }

    //根节点
    private Node root;

    //树中元素的个数
    private int size;

    public boolean isEmpty() {
        return size == 0;
    }

    public int getSize() {
        return size;
    }

    public void add(E e) {
        if (e == null) {
            throw new IllegalArgumentException("element is null.");
        }
        root = add(root, e);
    }

    private Node add(Node node, E e) {
        if (node == null) {
            size++;
            return new Node(e);
        }
        if (e.compareTo(node.e) < 0) {
            node.left = add(node.left, e);
        } else if (e.compareTo(node.e) > 0) {
            node.right = add(node.right, e);
        } else {
            //nothing to do
        }
        return node;
    }

    public boolean contains(E e) {
        if (e == null) {
            throw new IllegalArgumentException("element is null.");
        }
        return contains(root, e) != null;
    }

    private Node contains(Node node, E e) {
        if (node == null) {
            return null;
        }
        if (e.compareTo(node.e) < 0) {
            return contains(node.left, e);
        } else if (e.compareTo(node.e) > 0) {
            return contains(node.right, e);
        } else {
            return node;
        }
    }

    public E findMax() {
        if (root == null) {
            throw new IllegalArgumentException("tree is empty.");
        }
        return findMax(root).e;
    }

    private Node findMax(Node node) {
        Node ret = node;
        while (ret.right != null) {
            ret = ret.right;
        }
        return ret;
    }

    public E findMin() {
        if (root == null) {
            throw new IllegalArgumentException("tree is empty.");
        }
        return findMin(root).e;
    }

    private Node findMin(Node node) {
        Node ret = node;
        while (ret.left != null) {
            ret = ret.left;
        }
        return ret;
    }

    public void preTraversal() {
        preTraversal(root);
    }

    private void preTraversal(Node node) {
        if (node == null) {
            return;
        }
        System.out.print(node.e + " ");
        preTraversal(node.left);
        preTraversal(node.right);
    }

    public void inTranversal() {
        inTranversal(root);
    }

    private void inTranversal(Node node) {
        if (node == null) {
            return;
        }
        inTranversal(node.left);
        System.out.print(node.e + " ");
        inTranversal(node.right);
    }

    public void postTranversal() {
        postTranversal(root);
    }

    private void postTranversal(Node node) {
        if (node == null) {
            return;
        }
        postTranversal(node.left);
        postTranversal(node.right);
        System.out.print(node.e + " ");
    }

    public void levelTranversal() {
        Queue queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            Node poll = queue.poll();
            System.out.print(poll.e + " ");
            if (poll.left != null) {
                queue.offer(poll.left);
            }
            if (poll.right != null) {
                queue.offer(poll.right);
            }
        }
    }

    public E removeMax() {
        if (root == null) {
            throw new IllegalArgumentException("tree is empty.");
        }
        E max = findMax();
        removeMax(root);
        return max;
    }

    private Node removeMax(Node node) {
        if (node.right == null) {
            size--;
            return node.left;
        }
        node.right = removeMax(node.right);
        return node;
    }

    public E removeMin() {
        if (root == null) {
            throw new IllegalArgumentException("tree is empty.");
        }
        E min = findMin();
        removeMin(root);
        return min;
    }

    private Node removeMin(Node node) {
        if (node.left == null) {
            size--;
            return node.right;
        }
        node.left = removeMin(node.left);
        return node;
    }

    public void remove(E e) {
        if (root == null) {
            throw new IllegalArgumentException("tree is empty.");
        }
        root = remove(root, e);
    }

    private Node remove(Node node, E e) {
        if (node == null) {
            throw new IllegalArgumentException("not contains: " + e);
        }
        if (e.compareTo(node.e) < 0) {
            node.left = remove(node.left, e);
            return node;
        } else if (e.compareTo(node.e) > 0) {
            node.right = remove(node.right, e);
            return node;
        } else {
            if (node.left != null && node.right != null) {
                //删除的节点有左右子树
                //选择右子树的最小值节点或者左子树的最大值节点作为替换要删除的节点。
                Node newNode = findMax(node.right);
                newNode.right = removeMin(node.right);
                newNode.left = node.left;
                //for gc
                node.left = node.right = null;
                return newNode;
            } else if (node.left != null) {
                //删除的节点只有左子树
                return node.left;
            } else if (node.right != null) {
                //删除的节点只有右子树
                return node.right;
            } else {
                //删除的是叶子节点
                return null;
            }
        }
    }
}