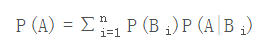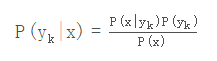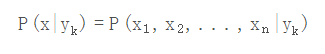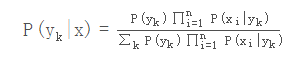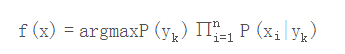机器学习算法——朴素贝叶斯

        朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法，对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对于给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用的方法。

朴素贝叶斯算法核心就两个： 

• 贝叶斯定理
• 朴素：假设各个特征之间是独立的

1. 朴素贝叶斯的理论基础（参考李航课本）

朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法。

这里提到的贝叶斯定理、特征条件独立假设就是朴素贝叶斯的两个重要的理论基础。

1.1 贝叶斯定理

先看什么是条件概率。

P(A|B)表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：

                                  

贝叶斯定理便是基于条件概率，通过P(A|B)来求P(B|A)：

                                 

上式中的分母P(A),可以根据全概率公式分解为：

                               

---

1.2 特征条件独立假设

这一部分开始朴素贝叶斯的理论推导，从中你会深刻地理解什么是特征条件独立假设。

给定训练数据集（X,Y），其中每个样本x都包括n维特征，即x=(x1,x2,x3,...,xn)，类标记集合含有k种类别，即y=(y1,y2,...,yk)

     。如果现在来了一个新样本x，我们要怎么判断它的类别？从概率的角度来看，这个问题就是给定x，它属于哪个类别的概率最大。那么问题就转化为求

                              

中最大的那个，即求后验概率最大的输出：

      argmaxykP(yk|x)

那P(yk|x)

怎么求解？答案就是贝叶斯定理：

根据全概率公式，可以进一步地分解上式中的分母：

先不管分母，分子中的P(yk)

是先验概率，根据训练集就可以简单地计算出来。而条件概率

  

 它的参数规模是指数数量级别的，假设第i维特征

xi可取值的个数有 Si个，类别取值个数为k个，那么参数个数为： k∏ni=1Si

这显然不可行。针对这个问题，朴素贝叶斯算法对条件概率分布作出了独立性的假设，通俗地讲就是说假设各个维度的特征x1,x2,...,xn互相独立，在这个假设的前提上，条件概率可以转化为：

                         P(x|yk)=P(x1,x2,...,xn|yk)=∏ni=1P(xi|yk) 

我们继续上面关于P(yk|x)的推导，得到  

于是朴素贝叶斯分类器可表示为：

因为对所有的yk

，上式中的分母的值都是一样的（为什么？注意到全加符号就容易理解了），所以可以忽略分母部分，朴素贝叶斯分类器最终表示为：

2、三种模型

多项式模型　MultinomialNB   也叫拉普拉斯修正

　　　　　多项式模型在计算先验概率P(yk)和条件概率P(x∣yk)时，会做一些平滑处理。文本分类，多项式模型中，重复出现的词语

在统计和判断时都视为出现了多次。

　　　　　　　　先验概率：某一类别出现的概率。 

　　　　　　　　　　　 Nyk ：类别为 yk 的样本个数

　　　　　　　　　　　N：样本总数

　　　　　　　　　　　k：类别数

　　　　　　　　　　　α：平滑值

　　　　　　　　条件概率：某一类别下某一特征出现的概率。 

　　　　　　　　　　　　Nyk：类别为yk的样本个数

　　　　　　　　　　　　n：特征数

　　　　　　　　　　　　α：平滑值

　　　　　　　　　　　　Nyk,xi：类别为yk的类别中，第i维特征，特征值为xi的样本数。

　　　　　　　　当α=1，叫拉普拉斯平滑(Laplace smothing)

　　　　　　　　当α=0，不做平滑，可能会导致条件概率P(x∣yk)为0。因为P(xi∣yk)可能为0。

　　　　　　　　当α=1，叫Lidstone 平滑

---

高斯模型

　　　　　特征维连续变量，如特征为人的身高、体重，用多项式模型容易导致P(x∣yk)为0(当α=0时)，即使做平滑，此时的条件概

率也难以描述真实情况。此时应使用高斯模型。高斯模型假设每一维特征符合高斯分布，也叫正态分布。高斯模型根据每一维的均值、方

差，得到每一维的密度函数，根据密度函数就可以得到当前维度值的密度函数值，以密度值作为条件概率的值。

　　　　　　　　条件概率 

P(xi|yk)=12πσ2yk,i−−−−−√e−(xi−μyk,i)22σ2yk,i

　　　　　　　　　　　　 P(xi|yk) ：类别 yk 中，第 i 维特征，特征值为 xi 的概率。

　　　　　　　　　　　　σyk,i：类别yk中，第i维特征的方差。

　　　　　　　　　　　　μyk,i：类别yk中，第i维特征的均值。

---

伯努利模型BernoulliNB

　　　　　与多项式模型一样，伯努利模型也适合离散特征。伯努利模型的每个特征的值只能是true和false，或者1和0,即特征有没有在

一个文档中出现。文本分类，伯努利模型中，重复出现的词语在统计和判断时都视为出现了一次。方便，但丢失了词频信息。

　　　　　　　　条件概率

　　　　　　　　　　　当特征值xi=1 

P(xi∣yk)=P(xi=1∣yk)

　　　　　　　　　　　当特征值 xi =0 

P(xi∣yk)=1−P(xi=1∣yk)

　　　　　　　　　　　 P(xi|yk) ：类别 yk 中，第 i 维特征，特征值为 xi 的概率。

3、 朴素贝叶斯分类的优缺点

优点：

（1） 算法逻辑简单,易于实现（算法思路很简单，只要使用贝叶斯公式转化医学即可！）

（2）分类过程中时空开销小（假设特征相互独立，只会涉及到二维存储）

缺点：

理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。

而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

参考博客： 点击打开链接， 点击打开链接， 点击打开链接