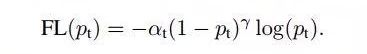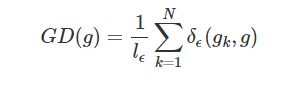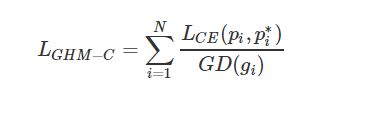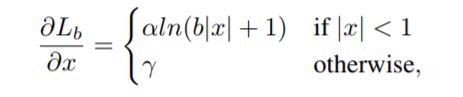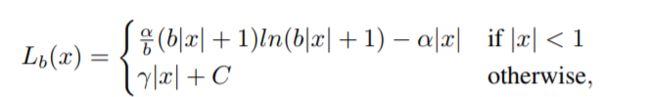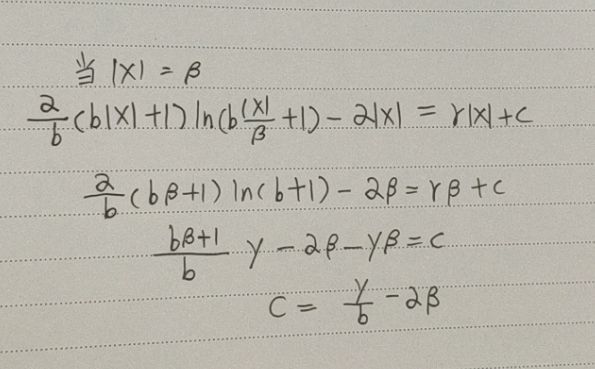【MMDetection 系列：三】Loss 函数详解 + Pytorch 实现

Reference

https://zhuanlan.zhihu.com/p/40284001
https://blog.csdn.net/weixin_41665360/article/details/100126744
https://github.com/open-mmlab/mmdetection
https://github.com/thangvubk/Cascade-RPN （based on mmdetection framework）
Deep Learning v1 笔记

一个函数能够作为损失函数，要符合以下两个特性：

• 非负
• 当实际输出接近预期，那么损失函数应该接近0

基本 loss

MSE —— 回归loss

参考KL散度

MSE 回归loss ，更适合用来预测值。而CE是衡量两个分布距离的指标

SSE

和方差

• 该参数计算的是拟合数据和原始对应点的误差的平方和

是真实数据， 是拟合的数据， ，从这里可以看出SSE接近于0，说明模型选择和拟合更好，数据预测也越成功。

MSE

均方方差

• 预测数据和原始数据对应点误差的平方和的均值
  

缺点

• 其偏导值在输出概率值接近0或者接近1的时候非常小，这可能会造成模型刚开始训练时，偏导值几乎消失。

import torch.nn.functional as F
mse_loss = weighted_loss(F.mse_loss)

RMSE

也叫回归系统的拟合标准差，是MSE的平方根，计算公式为：

0-1 Loss

0-1损失函数直接对应分类判断错误的个数，但是它是一个非凸函数，不太适用.

hinge loss

Hinge Loss常作为 SVM 的损失函数

L1 loss

L2 Loss

L2-loss 比 L1-loss 好，因为L2-loss的收敛速度要比L1-loss要快得多。

缺点：

• 当存在离群点（outliers)的时候，这些点会占loss的主要组成部分
  比如说真实值为1，预测10次，有一次预测值为1000，其余次的预测值为1左右，显然loss值主要由1000主宰

不管是L1损失函数，还是L2损失函数，都有两大缺陷：

• 假定噪声的影响和图像的局部特性是独立的。然而，人类的视觉系统对噪声的感知受局部照度、对比、结构的影响。
• 假定噪声接近高斯白噪声，然而这一假定并不总是成立。

分类 loss CE

CE

Cross - Entropy

交叉熵

表示样本， 表示预测的输出， 表示实际的输出， 表示样本总数量

• 对数似然函数，可用于二分类和多分类任务中
• 二分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）
• 多分类问题中的loss函数（输入数据是softmax或者sigmoid函数的输出）

交叉熵

def cross_entropy(pred, label, weight=None, reduction='mean', avg_factor=None):
    # element-wise losses
    loss = F.cross_entropy(pred, label, reduction='none')

    # apply weights and do the reduction
    if weight is not None:
        weight = weight.float()
    loss = weight_reduce_loss(
        loss, weight=weight, reduction=reduction, avg_factor=avg_factor)

    return loss

Binary CE loss

二分类

def binary_cross_entropy(pred,
                         label,
                         weight=None,
                         reduction='mean',
                         avg_factor=None):
    if pred.dim() != label.dim():
        label, weight = _expand_binary_labels(label, weight, pred.size(-1))

    # weighted element-wise losses
    if weight is not None:
        weight = weight.float()
    loss = F.binary_cross_entropy_with_logits(pred, label.float(), weight, reduction='none')
    # do the reduction for the weighted loss
    loss = weight_reduce_loss(loss, reduction=reduction,avg_factor=avg_factor)

    return loss

Balanced CE loss

类别不平衡问题对最终training loss的不利影响，我们自然会想到可通过在loss公式中使用与目标存在概率成反比的系数对其进行较正

Focal Loss

• RetinaNet 提出

  

• 指数式系数可对正负样本对loss的贡献自动调节
  当某样本类别比较明确些，它对整体loss的贡献就比较少；而若某样本类别不易区分，则对整体loss的贡献就相对偏大

• 引入了一个新的 hyper parameter 即 $\gamma$
  作者有试者对其进行调节，线性搜索后得出将γ设为2时，模型检测效果最好。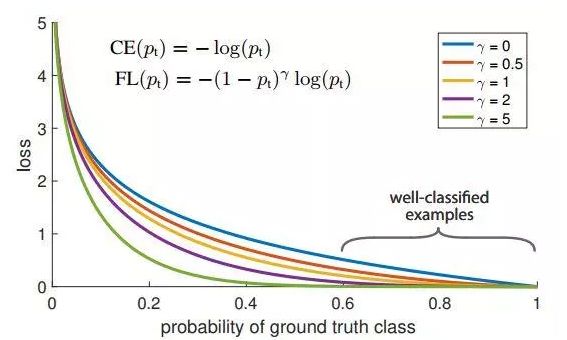

  

• 作者还引入了α系数，它能够使得focal loss对不同类别更加平衡
  

# This method is only for debugging
def py_sigmoid_focal_loss(pred,
                          target,
                          weight=None,
                          gamma=2.0,
                          alpha=0.25,
                          reduction='mean',
                          avg_factor=None):
    pred_sigmoid = pred.sigmoid()
    target = target.type_as(pred)
    pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)  
    '''
    pt 平衡难易例
     (alpha * target + (1 - alpha)*(1 - target)) 平衡正负例
    '''
    focal_weight = (alpha * target + (1 - alpha)*(1 - target)) *pt.pow(gamma)
    loss = F.binary_cross_entropy_with_logits(pred, target, reduction='none') * focal_weight
    loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
    return loss

ghm loss

https://arxiv.org/abs/1811.05181
https://www.cnblogs.com/xxxxxxxxx/p/11602248.html
https://blog.csdn.net/u013841196/article/details/88650784

• focal loss 的改进

  • focal loss 缺点
    • 如果让模型过多关注 难分样本 会引发一些问题，比如样本中的离群点（outliers），已经收敛的模型可能会因为这些离群点还是被判别错误，总而言之，我们不应该过多关注易分样本，但也不应该过多关注难分样本；
    • α 与 γ 的取值全从实验得出，且两者要联合一起实验，因为它们的取值会相互影响。

• 为了解决特别难分样本的问题

• 抑制方法之梯度密度 G(D)

  因为易分样本和特别难分样本数量都要比一般样本多一些，而我们要做的就是衰减 单位区间数量多的那类样本，也就是物理学上的密度概念

  

  

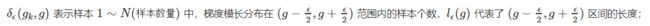
• 分类问题的GHM损失

• 回归问题的GHM损失

  

  为修正的 smooth L1 Loss

回归 loss —— L1

Smooth L1 loss （回归常用）

• faster rcnn 提出

优点

• 相比于L2损失函数，其对离群点、异常值（outlier）不敏感，梯度变化相对更小，训练时不容易跑飞

def smooth_l1_loss(pred, target, beta=1.0):
    assert beta > 0
    assert pred.size() == target.size() and target.numel() > 0
    diff = torch.abs(pred - target)
    loss = torch.where(diff < beta, 0.5 * diff * diff / beta,diff - 0.5 * beta)    
    '''
    torch.where  判断
    如果 diff
    return loss

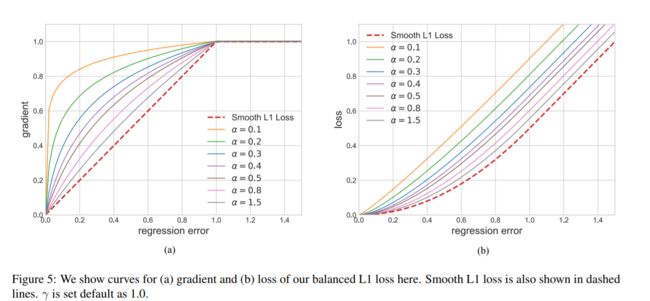
Balance L1 loss

• libra RCNN 提出

$α = 0.5$ and $γ = 1.5$

• C
  求解利用函数连续性,当x=beta（一般为1）时,公式 $L_b(x)$ 相等：
  

def balanced_l1_loss(pred,
                     target,
                     beta=1.0,
                     alpha=0.5,
                     gamma=1.5,
                     reduction='mean'):
    assert beta > 0
    assert pred.size() == target.size() and target.numel() > 0

    diff = torch.abs(pred - target)
    b = np.e**(gamma / alpha) - 1
    loss = torch.where(diff < beta, alpha / b *(b * diff + 1) * torch.log(b * diff / beta + 1) - alpha * diff,gamma * diff + gamma / b - alpha * beta)
    '''
    torch.where  判断
    如果 diff
    return loss

Bounded IOU loss

• GARPN 中使用

• 和 IOU loss 一样是 尺度不敏感

• 是 smooth L1 的改进，和IOU loss 没啥关系

@weighted_loss
def bounded_iou_loss(pred, target, beta=0.2, eps=1e-3):
    """Improving Object Localization with Fitness NMS and Bounded IoU Loss,
    https://arxiv.org/abs/1711.00164.
    Args:
        pred (tensor): Predicted bboxes.
        target (tensor): Target bboxes.
        beta (float): beta parameter in smoothl1.
        eps (float): eps to avoid NaN.
    """
    pred_ctrx = (pred[:, 0] + pred[:, 2]) * 0.5
    pred_ctry = (pred[:, 1] + pred[:, 3]) * 0.5
    pred_w = pred[:, 2] - pred[:, 0] + 1
    pred_h = pred[:, 3] - pred[:, 1] + 1
    with torch.no_grad():
        target_ctrx = (target[:, 0] + target[:, 2]) * 0.5
        target_ctry = (target[:, 1] + target[:, 3]) * 0.5
        target_w = target[:, 2] - target[:, 0] + 1
        target_h = target[:, 3] - target[:, 1] + 1

    dx = target_ctrx - pred_ctrx
    dy = target_ctry - pred_ctry

    loss_dx = 1 - torch.max(
        (target_w - 2 * dx.abs()) /
        (target_w + 2 * dx.abs() + eps), torch.zeros_like(dx))
    loss_dy = 1 - torch.max(
        (target_h - 2 * dy.abs()) /
        (target_h + 2 * dy.abs() + eps), torch.zeros_like(dy))
    loss_dw = 1 - torch.min(target_w / (pred_w + eps), pred_w /
                            (target_w + eps))
    loss_dh = 1 - torch.min(target_h / (pred_h + eps), pred_h /
                            (target_h + eps))
    loss_comb = torch.stack([loss_dx, loss_dy, loss_dw, loss_dh],
                            dim=-1).view(loss_dx.size(0), -1)

    loss = torch.where(loss_comb < beta, 0.5 * loss_comb * loss_comb / beta,
                       loss_comb - 0.5 * beta)
    return loss

回归 loss —— IoU

IOU Loss

• UnitBox 提出（做人脸）
  

• FCOS 等 anchor free 基本都用

• 求 IOU ，IOU 越大 loss 越小，IOU 越小 loss 越大

• 但是 他和 smooth L1 区别是 IOU loss 对尺寸大小不敏感

  

def iou_loss(pred, target, eps=1e-6):
    """IoU loss.
    Computing the IoU loss between a set of predicted bboxes and target bboxes.
    The loss is calculated as negative log of IoU.
    Args:
        pred (Tensor): Predicted bboxes of format (x1, y1, x2, y2),
            shape (n, 4).
        target (Tensor): Corresponding gt bboxes, shape (n, 4).
        eps (float): Eps to avoid log(0).
    Return:
        Tensor: Loss tensor.
    """
    ious = bbox_overlaps(pred, target, is_aligned=True).clamp(min=eps)
    loss = -ious.log()
    return loss

GIOU-loss

Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

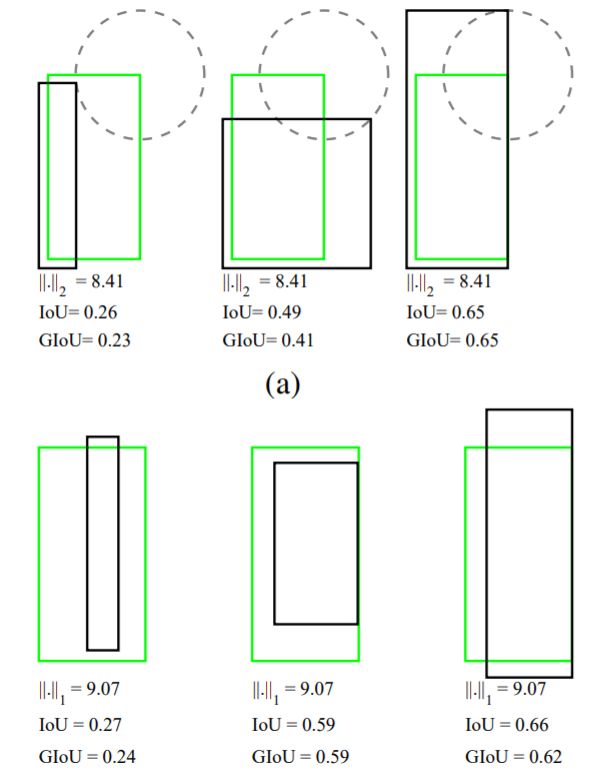
IOU Loss 缺点：

• 如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小（重合度）。同时因为loss=0，没有梯度回传，无法进行学习训练。
• IoU无法精确的反映两者的重合度大小。 GIOU是更严格的指标。
  以上几种情况下均有 IoU=0.33 IoU=0.33IoU=0.33 但是显然从左到右定位效果越来越差
  

GIoU

• 想法很好，效果一般，1-iou (Linear IOU loss) 基本可以达到1-giou（GIoU loss）相同的效果
• 成本高还不讨好，现在最广泛的基本就是线性IOUloss
• 闭包：包含两个框的最小框

Linear IOU Loss

$loss=1-ious$

def iou_loss(pred, target, linear=False, eps=1e-6):
    """IoU loss.
    Computing the IoU loss between a set of predicted bboxes and target bboxes.
   """
    ious = bbox_overlaps(pred, target, is_aligned=True).clamp(min=eps)
    if linear:
        loss = 1 - ious
    else:
        loss = -ious.log()
    return loss

分类概率

softmax （多分类）

https://zhuanlan.zhihu.com/p/25723112
https://www.zhihu.com/question/23765351/answer/240869755

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组 V，Vi表示V中的第i个元素，那么这个元素的Softmax值就是

Sigmoid （二分类）

$h(x)=\frac{1}{1+e^{-x}}$

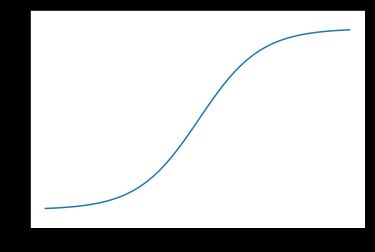
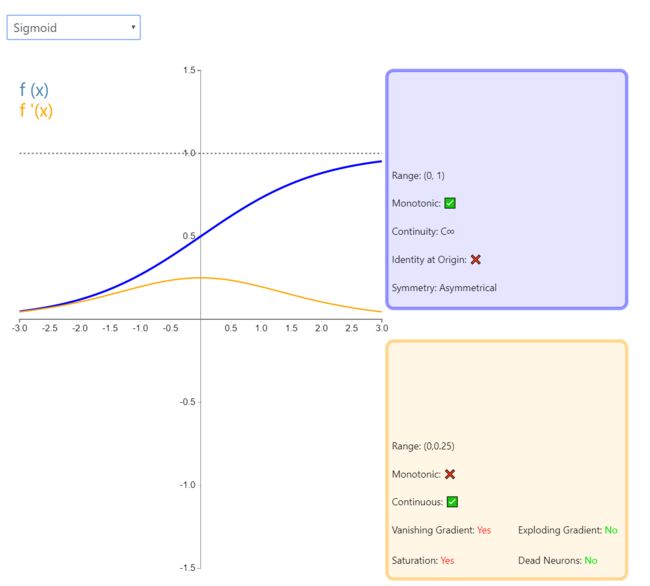
Sigmoid 因其在 logistic 回归中的重要地位而被人熟知，值域在 0 到 1 之间。Logistic Sigmoid（或者按通常的叫法，Sigmoid）激活函数给神经网络引进了概率的概念。它的导数是非零的，并且很容易计算（是其初始输出的函数）。然而，在分类任务中，sigmoid 正逐渐被 Tanh 函数取代作为标准的激活函数，因为后者为奇函数（关于原点对称）。

sigmoid函数缺点

• Sigmoid函数饱和使梯度消失。sigmoid神经元有一个不好的特性，就是当神经元的激活在接近0或1处时会饱和：在这些区域，梯度几乎为0。如果初始化权重过大，那么大多数神经元将会饱和，导致网络就几乎不学习了。

• Sigmoid函数的输出不是零中心的
  将影响梯度下降的运作