机器学习—线性回归模型(Linear regression)和逻辑回归模型(Logistics regression)
线性回归算法是基于连续变量预测特定结果的监督学习算法;Logistic回归专门用来预测离散值。
1. 线性回归模型(Linear regression)
线性回归模型是属于监督学习中的回归模型,也算是我学习过的模型中最简单的一个模型,其主要目的就是为了通过训练得到一个函数表达式来近似拟合平面内的所有离散的数据点,从而在新的数据输入进来时,能够给出预测值。
1.1 假设定义
![]()
其中![]() 表示最终的预测值,
表示最终的预测值,![]() 是权重,x表示数据或者特征,n表示的是输入数据的维度。
是权重,x表示数据或者特征,n表示的是输入数据的维度。![]() 要始终为1,这样
要始终为1,这样![]() 就是表示偏置值,我看吴恩达的机器学习视频的写法是这样,我认为这样做的目的是为了方便以后的矩阵运算。
就是表示偏置值,我看吴恩达的机器学习视频的写法是这样,我认为这样做的目的是为了方便以后的矩阵运算。
以预测房价这个问题为例子,我们需要根据房子的面积,户型,位置,交通等等因素来预测房子的价格。那么对应上式,房子的价格就是![]() ,面积,户型,位置,交通就是我们的特征,分别对应
,面积,户型,位置,交通就是我们的特征,分别对应![]() 。
。
1.2 Cost Function
关于Cost function的详细内容请看我以前的博客。(Cost function)
假设输入数据只有2个维度,则Cost Function如下
其中![]() 表示的是Cost值,
表示的是Cost值,![]() 表示的是在当前参数下,对于第i组数据的预测值,
表示的是在当前参数下,对于第i组数据的预测值,![]() 表示的是第i组数据的实际值,m表示训练数据的个数。
表示的是第i组数据的实际值,m表示训练数据的个数。
1.3 目的
得到表达式和Cost Function之后,我们现在的目的就是不断的迭代更新![]() ,使得J越来越小,J越来越小就表示
,使得J越来越小,J越来越小就表示![]() 能够越来越好的拟合所有的数据点。然后在测试数据输入进来时,利用
能够越来越好的拟合所有的数据点。然后在测试数据输入进来时,利用![]() 计算得到预测值。
计算得到预测值。
1.4 示例
上面都是一些纯理论知识,现在我将使用一个经典的例子来给大家实例化一下。
我们现在有一个需求就是要预测房价,为了表示简单,只有一个特征,即房子的面积。这时,根据上面的几个公式,我们用这几个符号表示数据:
 表示房子的面积,
表示房子的面积, 始终为1(为了使
始终为1(为了使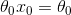 来表示偏置)
来表示偏置)- y表示房子的真实价格
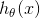 表示房子的预测价格
表示房子的预测价格
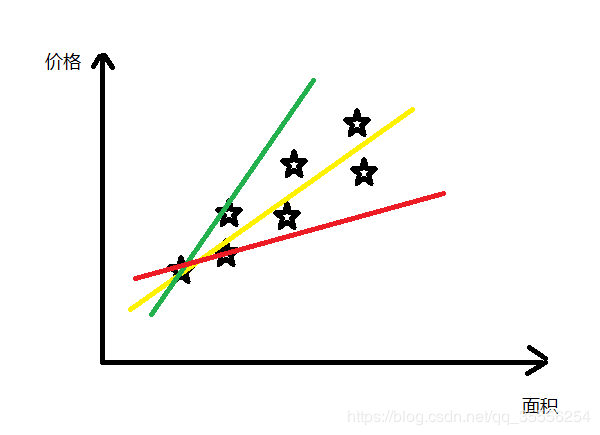
我们现在的目的就是得到公式![]() 来拟合上面的点,我们选用不同的参数会得到不同的直线
来拟合上面的点,我们选用不同的参数会得到不同的直线
由上图所示,选用三种不同的参数会得到三条不同的公式,从中很容易看出来黄色的线拟合数据的结果是最好的,至于怎么更新参数来得到最好的拟合效果,我在参数更新这篇博客中有详细介绍。
2 逻辑回归模型(Logistics regression)
针对分类问题,在之前提到的线性回归模型看来,可以将预测的结果映射到一个[0,1]区间内,大于0.5的结果可以看成(是),小于0.5的结果可以看成0(否)。但这通常效果不是很好,因为分类问题本来就不是一个线性问题。这就引出了逻辑回归模型。
所以这次我主要以二分类问题为例子来介绍一下逻辑回归。
2.1 数据格式和含义
我们还是以(x,y)来表示数据,x是特征与线性回归模型中的x是相同的;y是结果,与线性回归模型不同的是,这里的y不在是一个值,而是一个取值只能是0或1的变量(针对二分类问题),分别代表属于哪个类别。(如果要扩展到多分类问题,y可以取值0,1,2,3......,即有多少个类别就有多少个值)。
针对y的取值,我举个例子:当我们要设计一个区分一个物体是否是水果的系统,这是y的取值只能是0或1,分别代表“不是水果”和“是水果”这两个结果。
y也可以叫做训练数据的标签。
2.2 假设定义
每个模型针对不同的功能都要定义一个hypothesis来实现功能,上一次的线性回归模型的定义是 ![]()
![]() 最后求得的是一个确切的值,比如在预测房价问题中,其值代表的就是预测的房价。
最后求得的是一个确切的值,比如在预测房价问题中,其值代表的就是预测的房价。
针对分类问题,我们使用sigmoid函数来将![]() 的结果映射在(0,1)区间内,其公式为:
的结果映射在(0,1)区间内,其公式为:![]() sigmoid函数图像如下图所示:
sigmoid函数图像如下图所示:
从上图我们可以看到,y的取值范围一直是(0,1)。因此逻辑回归的hypothesis就是 ![]()
这里![]() 的意义就是结果为1的概率是多少。比如
的意义就是结果为1的概率是多少。比如![]() =0.7就是指结果为1的概率是70%。同时
=0.7就是指结果为1的概率是70%。同时![]() 满足以下公式
满足以下公式
![]()
![]()
2.3 决策边界(Decision boundary)
为了实现二分类问题,我们可以将hypothesis解释如下
![]()
![]()
2.4 Cost function
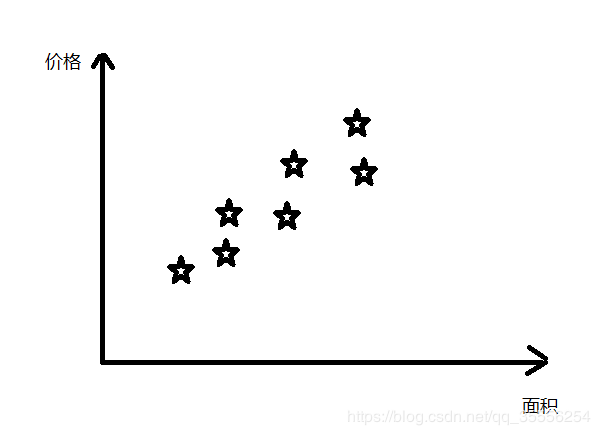
我们定义逻辑回归的Cost function如下:
![]() if y = 1
if y = 1
![]() if y = 0
if y = 0
将上面三条式子整合起来就可得到下面这条总的Cost function的式子
参数的更新方法也是利用梯度下降算法。具体内容可以参考我之前写的参数更新方法,这里就不再赘述。
2.5 多分类问题(Multiclass classification)
上面所有的东西都是基于二分类的问题,然而从二分类扩展到多分类问题是很简单的。
在多分类问题中,y的取值不再只是0和1,而可以表达为![]() 。然后我们再重定义一下hypothesis。
。然后我们再重定义一下hypothesis。
![]()
![]() 表示的是属于第i个结果的概率是多少。那么多分类问题就可以化解为多个二分类问题,即对每个类别做一次逻辑回归,得到属于该类别的概率,然后在n个类别中选择概率最大的那个类别来作为最后的结果。表达式为
表示的是属于第i个结果的概率是多少。那么多分类问题就可以化解为多个二分类问题,即对每个类别做一次逻辑回归,得到属于该类别的概率,然后在n个类别中选择概率最大的那个类别来作为最后的结果。表达式为
![]()
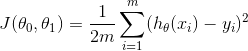


![J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]](http://img.e-com-net.com/image/info8/1537d2fb54f74c1ab90895f956fbbf37.gif)