线性模型（二）Fisher线性判别分析

线性判别分析，Linear Discriminant Analysis，一种用于二分类的很经典的线性学习方法，1936年由Fisher 提出，so也称为Fisher判别分析。它和PCA一样，也是一种降维方法。
英国大统计学家Fisher,“a genius who almost single-handedly created the foundations for modern statistical science”，“the single most important figure in 20th century statistics”.

LDA方法属于模式识别领域。
模式识别系统的基本构成：数据采集和预处理，特征选取，分类器设计，训练测试，计算分类结果，复杂度分析。
其中，选取特征是个技术活，如果特征过多，某些特征实际和分类结果相关性很小，就会造成过拟合，模型无法适用于新数据。不必要的特征甚至可能带来不可预知的影响。除此以外，过多的特征运算量也太大。因此，降维很必要。

---

（1）思想

训练阶段：通过投影进行降维，把所有带标签的训练数据点投影到一个直线（or低维超平面），使得两类数据点投影后的位置满足，类内离差最小，类间离差最大，即同类样本的投影点尽可能接近，异类样本的投影点尽可能远离。

贴一张周志华西瓜书的图：

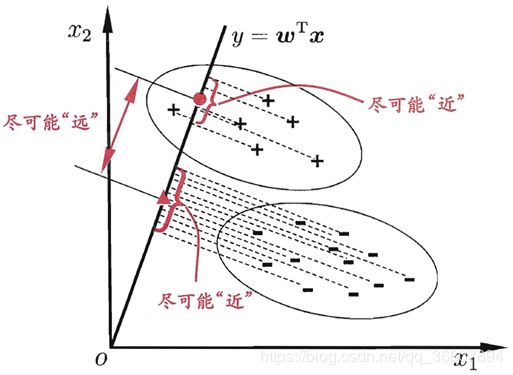
数据点都是二维的（2个特征），沿着虚线方向投影到那条直线，达到分离目的。所以，LDA的关键就是找这个投影方向。分界线的方程为$y={\mathbf{w}}^T\mathbf{x}$,投影方向与之正交，那自然就是$\mathbf{w}$的方向了。

测试阶段：把新数据点也投影到同一个低维超平面，根据投影点的位置判断类别。

（2）原理和推导

（不明白时结合上面的图去看）

（一）类内散布矩阵和类间散布矩阵

假设样本分两类，第0类和第1类，对应两个子集$X_0,X_1$，样本点总数分别是$N_0,N_1$

投影到的直线/低维超平面的方程是$y={\mathbf{w}}^T\mathbf{x}$

从核心思想的两个角度分别出发，建立部分的数学模型：

1. 类间距离尽可能大：

${\mathbf{\mu }}_0,{\mathbf{\mu }}_1$分别是两类样本的中心：

$${\mathbf{\mu }}_0=\frac{1}{N_0}\sum _{\mathbf{x}\in X_0}\mathbf{x}$$

$${\mathbf{\mu }}_1=\frac{1}{N_1}\sum _{\mathbf{x}\in X_1}\mathbf{x}$$

两个中心到直线上的投影分别为${\mathbf{w}}^T{\mathbf{\mu }}_0和{\mathbf{w}}^T{\mathbf{\mu }}_1$。

为了使类间距离最大，则应最大化这两个投影点之间的距离：
$$||{\mathbf{w}}^T{\mathbf{\mu }}_0-{\mathbf{w}}^T{\mathbf{\mu }}_1|{|}_2^2$$
即
$$||{\mathbf{w}}^T({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)|{|}_2^2=$$

$${\mathbf{w}}^T({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)[{\mathbf{w}}^T({\mathbf{\mu }}_0-{\mathbf{\mu }}_1){]}^T=$$

$${\mathbf{w}}^T({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^T\mathbf{w}=$$

$${\mathbf{w}}^T{S}_b\mathbf{w}$$

其中$S_b$为类间散布矩阵：

$$S_b=({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^T$$
S代表scatter（散布矩阵scatter matrix），b下标代表between，$S_b$表示between class scatter。

总结：最大化类间距离等同于最大化$${\mathbf{w}}^T{S}_b\mathbf{w}$$

2. 类内距离尽可能小：

$X_0和X_1$内数据点$x$投影后的点：${\mathbf{w}}^T\mathbf{x}$(这是个标量)
可以很自然的想到，定义投影后一个类的离散程度，可以用每个点到类的中心的距离的平方（一般都用距离的平方，不直接使用距离）之和。
即：
$$\sum _{\mathbf{x}\in X_0}({\mathbf{w}}^T(\mathbf{x}-{\mathbf{\mu }}_0){)}^2=\sum _{\mathbf{x}\in X_0}{\mathbf{w}}^T(\mathbf{x}-{\mathbf{\mu }}_0)({\mathbf{w}}^T(\mathbf{x}-{\mathbf{\mu }}_0){)}^T=$$
$$\sum _{\mathbf{x}\in X_0}{\mathbf{w}}^T(\mathbf{x}-{\mathbf{\mu }}_0)(\mathbf{x}-{\mathbf{\mu }}_0{)}^T\mathbf{w}={\mathbf{w}}^T[\sum _{\mathbf{x}\in X_0}(\mathbf{x}-{\mathbf{\mu }}_0)(\mathbf{x}-{\mathbf{\mu }}_0{)}^T]\mathbf{w}$$

两个类总的类内距离的平方则是：
$${\mathbf{w}}^T[\sum _{\mathbf{x}\in X_0}(\mathbf{x}-{\mathbf{\mu }}_0)(\mathbf{x}-{\mathbf{\mu }}_0{)}^T+\sum _{\mathbf{x}\in X_1}(\mathbf{x}-{\mathbf{\mu }}_1)(\mathbf{x}-{\mathbf{\mu }}_1{)}^T]\mathbf{w}$$

定义类内散布矩阵为：

$$S_w=S_0+S_1$$

其中$S_0,S_1$分别是两个类的类内散布矩阵：

$$S_0=\sum _{\mathbf{x}\in X_0}(\mathbf{x}-{\mu }_0)(\mathbf{x}-{\mu }_0{)}^T$$

$$S_1=\sum _{\mathbf{x}\in X_1}(\mathbf{x}-{\mu }_1)(\mathbf{x}-{\mu }_1{)}^T$$

总结起来,要最小化的两个类的总类内距离的平方可进一步写为：

$${\mathbf{w}}^T[S_0+S_1]\mathbf{w}={\mathbf{w}}^T{S}_w\mathbf{w}$$

（二）由代价函数/能量函数推出投影方向

有了前面两个概念作为基础，就可以进入最关键的能量函数推导了。

对（一）总结：

要最大化的类间距离：$${\mathbf{w}}^T{S}_b\mathbf{w}$$
要最小化的类内距离：$${\mathbf{w}}^T{S}_w\mathbf{w}$$
所以构造能量函数：
$$J=\frac{{\mathbf{w}}^T{S}_w\mathbf{w}}{{\mathbf{w}}^T{S}_b\mathbf{w}}$$

看这个函数的形式，这就是广义瑞利商（genralized Rayleigh quotient），研一的矩阵理论课程里学的瑞利商的推广形式。
所以LDA就转化为了$S_b和S_w$的广义瑞利商问题。

---

知识小补充：瑞利商

1. 瑞利商定义:
   $$R(A,x)=\frac{x^{H}Ax}{x^{H}x}$$
   其中x为非零向量，而A为n×n的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵，即$A^H=A$。如果我们的矩阵A是实矩阵，则满足$A^T=A$的矩阵即为Hermitan矩阵。
   瑞利商R(A,x)有一个非常重要的性质，即它的最大值等于矩阵A最大的特征值，而最小值等于矩阵A的最小的特征值，也就是满足
   $$\lambda min\le \frac{x^{H}Ax}{x^{H}x}\le \lambda max$$
   当向量x是标准正交基时，即满足$x^{H}x=1$时，瑞利商退化为：$R(A,x)=x^{H}Ax$，这个形式在谱聚类和PCA中都有出现。
2. 广义瑞利商定义:
   $$R(A,B,x)=\frac{x^{H}Ax}{x^{H}Bx}$$
   其中x为非零向量，A,B为n×n的Hermitan矩阵。B为正定矩阵。它的最大值和最小值是什么呢？其实我们只要通过将其通过标准化就可以转化为瑞利商的格式。我们令$x=B^{-1/2}y,$则分母转化为：
   $$x^{H}Bx=y^H(B^{-1/2}{)}^{H}B{B}^{-1/2}y=y^H{B}^{-1/2}B{B}^{-1/2}y=y^{H}y$$
   而分子转化为：
   $$x^{H}Ax=y^H{B}^{-1/2}A{B}^{-1/2}y$$
   此时我们的R(A,B,x)转化为R(A,B,y):
   $$R(A,B,y)=\frac{y^H{B}^{-1/2}A{B}^{-1/2}y}{y^{H}y}$$
   其中$B^{-1/2}=(B^{-1/2}{)}^H$,因为B是hermitan矩阵。
   令矩阵$M=B^{-1/2}A{B}^{-1/2}$
   则$$R(A,B,y)=\frac{y^{H}My}{y^{H}y}$$
   利用瑞利商的性质很快知道，R(A,B,x)的最大值为矩阵M的最大特征值。
   对M左乘$B^{-1/2}$,右乘$B^{1/2}$，也就是对M做个相似变换，得到矩阵$B^{-1}A$，相似变换特征值不变，所以也可以说R(A,B,x)的最大值为矩阵$B^{-1}A$的最大特征值，而最小值为矩阵$B^{-1}A$的最小特征值。

---

上面这段虽然长，但结论很简单:

广义瑞利商$R(A,B,x)=\frac{x^{H}Ax}{x^{H}Bx}$的最大值为矩阵$B^{-1}A$的最大特征值，而最小值为矩阵$B^{-1}A$的最小特征值。

so!!!

$$minJ=\frac{{\mathbf{w}}^T{S}_w\mathbf{w}}{{\mathbf{w}}^T{S}_b\mathbf{w}}$$
这个最优化问题的解就是$S_b^{-1}{S}_w$的最小特征值！！！
但可惜了，我们真正care的并不是能量函数的具体最小值是多大，而是使得能量函数取到最小值的那个权向量$w$。

所以还得继续想办法求$w$，但要知道求$w$,重点只是求它的方向，大小无所谓的，因为它的方向就是投影方向。

回到上面观察$S_b,S_w$,发现这两个矩阵只和数据有关，训练数据一旦确定他俩就完全确定了，成了常值矩阵，和$w$无关。

再观察能量函数，分子分母都有$w$，把$w$和$\alpha w$代入，能量函数的值一样，所以$J$只和$w$的方向有关，和具体长度无关。

那么比较技巧性的东西就来了。。。
归一化，令分母为1，这只是限制了$w$的大小而已。反正大小不重要。。问题转化为：

$$minJ={\mathbf{w}}^T{S}_w\mathbf{w}，s.t.{\mathbf{w}}^T{S}_b\mathbf{w}=1$$
有等式约束的最优化问题，自然又是要用拉格朗日乘子法了。引入拉格朗日乘子$\lambda$构造拉格朗日函数：

$$L（w,\lambda ）={\mathbf{w}}^T{S}_w\mathbf{w}-\lambda ({\mathbf{w}}^T{S}_b\mathbf{w}-1)$$

对$w$求偏导令为0。

$$2S_{w}w-2\lambda S_{b}w=0$$
即$$S_{w}w=\lambda S_{b}w$$
也就是说，矩阵$S_w$表示的变换和矩阵$S_b$表示的变换作用于$w$后得到的向量在一条线上，方向相同。那在什么方向呢？注意到$S_b\mathbf{w}=({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^T\mathbf{w}$的方向恒为${\mathbf{\mu }}_0-{\mathbf{\mu }}_1$,因为后两项乘积是个标量。that’s to say,$S_{w}w$也在${\mathbf{\mu }}_0-{\mathbf{\mu }}_1$方向上！！！
既然$S_w$表示的变换作用在$w$上把它旋转到了${\mathbf{\mu }}_0-{\mathbf{\mu }}_1$方向，那再把它的逆变换$S_w^{-1}$作用到${\mathbf{\mu }}_0-{\mathbf{\mu }}_1$上，不就回到$w$方向啦！！

不管$w$的大小，所以：
$$\mathbf{w}=S_w^{-1}({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)$$

求解完毕！！！！！开心!!

投影的方向只由$S_w$和两个类的中心决定。

在实际求解中，由于矩阵求逆很难，所以通常对$S_w$进行奇异值分解，$S_w=U\Sigma V^T$
则$S_w^{-1}=V{\Sigma }^{-1}{U}^T$.

（三）新数据的投影和分类

这就很简单了。。
新数据$x^{\ast }$的投影点：$${\mathbf{w}}^T{x}^{\ast }$$

判别数据点属于第0类还是第1类的阈值：
$$w_0=\frac{w^T{\mu }_0+w^T{\mu }_1}{2}$$

或者

$$w_0=\frac{N_0{w}^T{\mu }_0+N_1{w}^T{\mu }_1}{N_0+N_1}$$

我觉得第二种更加准确，毕竟考虑了两类样本数目的影响。

若${\mathbf{w}}^T{x}^{\ast }>w_0$,则新样本属于第0类
若${\mathbf{w}}^T{x}^{\ast }<w_0$,则新样本属于第1类

---

附注：

很多博客，包括老师课件都是把能量函数写成$$J=\frac{{\mathbf{w}}^T{S}_b\mathbf{w}}{{\mathbf{w}}^T{S}_w\mathbf{w}}$$
需要最大化这个能量函数，后面问题转化为
$$minJ=-{\mathbf{w}}^T{S}_b\mathbf{w},s.t.{\mathbf{w}}^T{S}_w\mathbf{w}=1$$

再用拉格朗日乘子法，虽然和我的过程略有不同，但思想和结果是完全一样的。我仔细想了想，觉得两种应该都可以，大家在LDA问题都习惯于用最大化的能量函数可能因为从最开始就这样，不是因为我那样做是错的，因为根据物理意义，能量函数的分子分母都不可能为0，所以两种都正确。