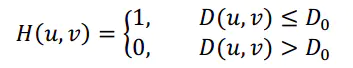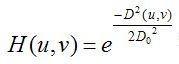图像预处理流程与方法

图像分析中，图像质量的好坏直接影响识别算法的设计与效果的精度，因此在图像分析（特征提取、分割、匹配和识别等）前，需要进行预处理。图像预处理的主要目的是消除图像中无关的信息，恢复有用的真实信息，增强有关信息的可检测性、最大限度地简化数据，从而改进特征提取、图像分割、匹配和识别的可靠性。
一般的预处理流程为：灰度化->几何变换->图像增强

一、灰度化

对彩色图像进行处理时，我们往往需要对三个通道依次进行处理，时间开销将会很大。因此，为了达到提高整个应用系统的处理速度的目的，需要对彩色图像进行灰度化以减少所需处理的数据量。
在RGB模型中，如果R=G=B时，则彩色表示一种灰度颜色，其中R=G=B的值叫灰度值，因此，灰度图像每个像素只需一个字节存放灰度值（又称强度值、亮度值），灰度范围为0-255。一般有分量法、最大值法、平均值法、加权平均法四种方法对彩色图像进行灰度化。

加权平均法

根据重要性及其它指标，将三个分量以不同的权值进行加权平均。由于人眼对绿色的敏感最高，对蓝色敏感最低，因此，按下式对RGB三分量进行加权平均能得到较合理的灰度图像。

转换算法 L = R * 299/1000 + G * 587/1000+ B * 114/1000

二、几何变换

图像几何变换又称为图像空间变换，通过平移、转置、镜像、旋转、缩放等几何变换对采集的图像进行处理，用于改正图像采集系统的系统误差和仪器位置（成像角度、透视关系乃至镜头自身原因）的随机误差。此外，还需要使用灰度插值算法，因为按照这种变换关系进行计算，输出图像的像素可能被映射到输入图像的非整数坐标上。通常采用的方法有最近邻插值、双线性插值和双三次插值。

1、最近邻插值

# coding = utf-8
"""
最近邻插值图像缩放演示
"""
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl

def func(x, y):
    return (x+y)*np.exp(-5.0*(x**2 + y**2))

# X-Y轴分为15*15的网格
y,x= np.mgrid[-1:1:15j, -1:1:15j]

fvals = func(x,y) # 计算每个网格点上的函数值  15*15的值

#三次样条二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')

# 计算100*100的网格上的插值
xnew = np.linspace(-1,1,100)#x
ynew = np.linspace(-1,1,100)#y
fnew = newfunc(xnew, ynew)#仅仅是y值   100*100的值

# 绘图
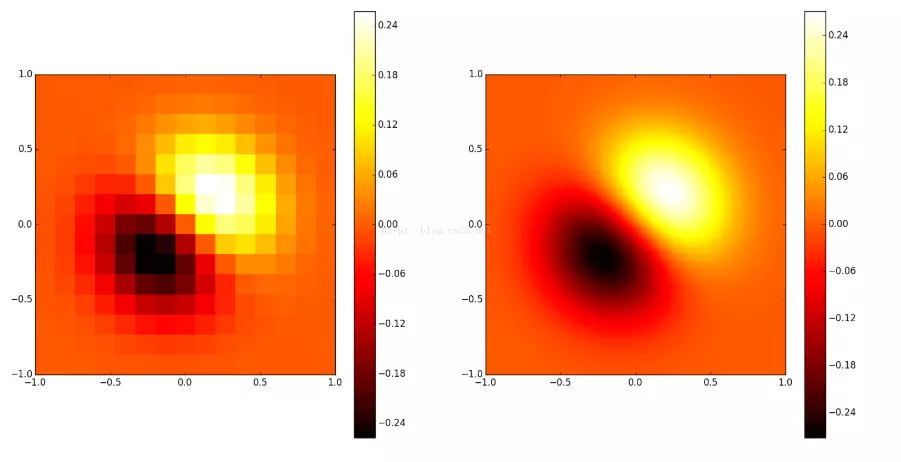
# 为了更明显地比较插值前后的区别，使用关键字参数interpolation='nearest'
# 关闭imshow()内置的插值运算。
pl.subplot(121)
im1=pl.imshow(fvals, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")#pl.cm.jet
pl.colorbar(im1)

pl.subplot(122)
im2=pl.imshow(fnew, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im2)
pl.show()

2、双线性插值

# encoding: utf-8
'''
双线性插值图像缩放算法
'''
import numpy as np
import cv2 as cv
import math

def bi_linear(src, dst, target_size):
    pic = cv.imread(src)       # 读取输入图像
    th, tw = target_size[0], target_size[1]
    emptyImage = np.zeros(target_size, np.uint8)
    for k in range(3):
        for i in range(th):
            for j in range(tw):
                # 首先找到在原图中对应的点的(X, Y)坐标
                corr_x = (i+0.5)/th*pic.shape[0]-0.5
                corr_y = (j+0.5)/tw*pic.shape[1]-0.5
                point1 = (math.floor(corr_x), math.floor(corr_y))   # 左上角的点
                point2 = (point1[0], point1[1]+1)
                point3 = (point1[0]+1, point1[1])
                point4 = (point1[0]+1, point1[1]+1)

                fr1 = (point2[1]-corr_y)*pic[point1[0], point1[1], k] + (corr_y-point1[1])*pic[point2[0], point2[1], k]
                fr2 = (point2[1]-corr_y)*pic[point3[0], point3[1], k] + (corr_y-point1[1])*pic[point4[0], point4[1], k]
                emptyImage[i, j, k] = (point3[0]-corr_x)*fr1 + (corr_x-point1[0])*fr2

    cv.imwrite(dst, emptyImage)

def main():
    src = 'pic/raw_1.jpg'
    dst = 'pic/new_1.png'
    target_size = (300, 200, 3)     # 变换后的图像大小

    bi_linear(src, dst, target_size)

if __name__ == '__main__':
    main()

三、图像增强

增强图像中的有用信息，它可以是一个失真的过程，其目的是要改善图像的视觉效果，针对给定图像的应用场合，有目的地强调图像的整体或局部特性，将原来不清晰的图像变得清晰或强调某些感兴趣的特征，扩大图像中不同物体特征之间的差别，抑制不感兴趣的特征，使之改善图像质量、丰富信息量，加强图像判读和识别效果，满足某些特殊分析的需要。
图像增强可分成两大类：频率域法和空间域法。

1、频率域法

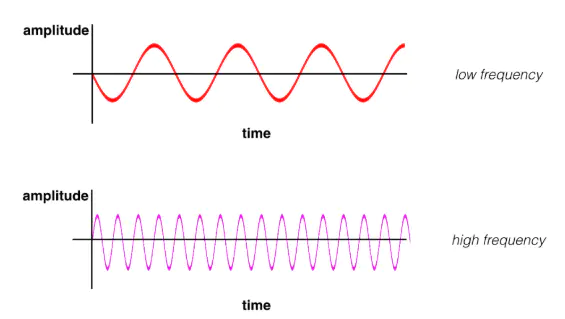
我们知道声音的频率是什么意思。高频是指音调很高的噪音，例如鸟的唧唧声或小提琴的声音。低频是指音调很低的声音，例如深沉的声音或低音鼓。对于声音来说，频率是指声波的振荡速度；振荡通常以周期 (Hz) 表示，高音调由高频声波组成。低频和高频声波的示例如下图所示。在 y 轴上是振幅，即声压相对于声音感知音量的测量结果；x 轴是时间。

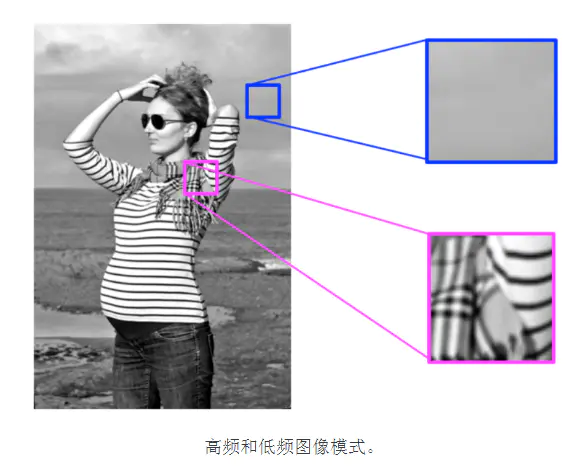
同样，图像中的频率是指变化速度。但是图像的变化是什么意思？图像会在空间中变化，高频图像是指强度变化很多的图像。亮度水平从一个像素到另一个像素变化很快。低频图像可能是亮度比较均匀或变化很慢的图像。

 

 

大多数图像同时具有高频和低频部分。在上图中，丝巾和条纹衬衫部分是高频图像模式；此部分非常快速地从一个亮度变成另一个亮度。在同一图像的更上方，我们看到天空和背景变化很缓慢，称为平滑的低频模式。
频率域法是一种间接图像增强算法，把图像看成一种二维信号，对其进行基于二维傅里叶变换的信号增强。采用低通滤波（即只让低频信号通过）法，可去掉图中的噪声；采用高通滤波法，则可增强边缘等高频信号，使模糊的图片变得清晰。

 

图像的傅里叶变换
进行傅立叶变换（FT）后，可以显示图像的频率分量。

# coding = utf-8
import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv

def ft_image(norm_image):
    '''
    二维傅里叶变换，接收一个灰度化且归一化的图像返回图像的频谱变换图
    '''
    f = np.fft.fft2(norm_image)
    fshift = np.fft.fftshift(f)
    frequency_tx = 20*np.log(np.abs(fshift))
    
    return frequency_tx

# 图像读取并灰度化
image_stripes = cv.imread('images/stripes.jpg')
image_stripes = cv.cvtColor(image_stripes, cv.COLOR_BGR2RGB)
gray_stripes = cv.cvtColor(image_stripes, cv.COLOR_RGB2GRAY)

image_solid = cv.imread('images/pink_solid.jpg')
image_solid = cv.cvtColor(image_solid, cv.COLOR_BGR2RGB)
gray_solid = cv.cvtColor(image_solid, cv.COLOR_RGB2GRAY)

# 为了便于后续处理将颜色空间从 [0,255] 归一化到 [0,1]
norm_stripes = gray_stripes/255.0
norm_solid = gray_solid/255.0

# 生成频谱图
f_stripes = ft_image(norm_stripes)
f_solid = ft_image(norm_solid)

# 可视化
f, (ax1,ax2,ax3,ax4) = plt.subplots(1, 4, figsize=(20,10))

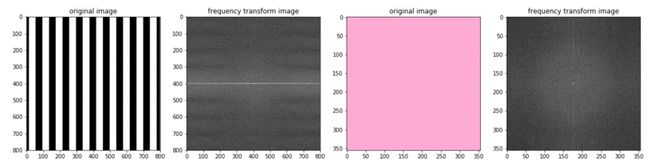
ax1.set_title('original image')
ax1.imshow(image_stripes)
ax2.set_title('frequency transform image')
ax2.imshow(f_stripes, cmap='gray')

ax3.set_title('original image')
ax3.imshow(image_solid)
ax4.set_title('frequency transform image')
ax4.imshow(f_solid, cmap='gray')

图像处理与二维傅里叶变换
二维频谱中的每一个点都是一个与之一一对应的二维正弦/余弦波。
拓展阅读

（1）理想的高/低通滤波

顾名思义，低通滤波器为：让低频信息通过，过滤高频信息

其中，D0表示通带半径，D(u，v)是到频谱中心的距离（欧式距离），计算公式如下：

M和N表示频谱图像的大小，（M/2，N/2）即为频谱中心
tips：高通滤波器与此相反，1减去低通滤波模板即可

def make_transform_matrix(image_arr, d0, ftype):
    '''
    构建理想高/低通滤波器
    INPUT  -> 图像数组, 通带半径, 类型
    '''
    transfor_matrix = np.zeros(image_arr.shape, dtype=np.float32)  # 构建滤波器
    w, h = transfor_matrix.shape
    for i in range(w):
        for j in range(h):
            distance = np.sqrt((i - w/2)**2 + (j - h/2)**2)
            if distance < d0:
                transfor_matrix[i, j] = 1
            else:
                transfor_matrix[i, j] = 0
    if ftype == 'low':
        return transfor_matrix
    elif ftype == 'high':
        return 1 - transfor_matrix
    
# 图像灰度化
img_arr = np.array(Image.open('33.jpg').convert('L'))

# 将图像从空间域转换到频率域
f = np.fft.fft2(img_arr)
fshift = np.fft.fftshift(f)

# 生成低通滤波器
F_filter1 = make_transform_matrix(img_arr, 30, 'low')
# 滤波
result = fshift*F_filter1
# 将图像从频率域转换到空间域
img_d1 = np.abs(np.fft.ifft2(np.fft.ifftshift(result)))

# 可视化
plt.imshow(array_to_image(img_d1))
plt.show()

（2）高斯高/低通滤波

Guassian低通滤波器函数为

tips： 1减去低通滤波模板即可得到高通滤波模板

def make_transform_matrix(image_arr, d0, ftype='low'):
    '''
    构建高斯高/低通滤波
    INPUT  -> 图像数组, 通带半径, 类型
    '''
    transfor_matrix = np.zeros(image_arr.shape, dtype=np.float32)  # 构建滤波器
    w, h = image_arr.shape
    for i in range(w):
        for j in range(h):
            distance = np.sqrt((i - w/2)**2 + (j - h/2)**2)
            transfor_matrix[i, j] = np.e ** (-1 * (distance ** 2 / (2 * d0 ** 2)))  # Gaussian滤波函数
    if ftype == 'low':
        return transfor_matrix
    elif ftype == 'high':
        return 1 - transfor_matrix

    
# 图像灰度化
img_arr = np.array(Image.open('33.jpg').convert('L'))

# 将图像从空间域转换到频率域
f = np.fft.fft2(img_arr)
fshift = np.fft.fftshift(f)

# 生成低通滤波器
F_filter1 = make_transform_matrix(img_arr, 30, 'low')
# 滤波
result = fshift*F_filter1
# 将图像从频率域转换到空间域
img_d1 = np.abs(np.fft.ifft2(np.fft.ifftshift(result)))

# 可视化
plt.imshow(array_to_image(img_d1))
plt.show()

2、空间域法

空间域法是一种直接图像增强算法，分为点运算算法和邻域去噪算法。
点运算算法即灰度变换（伽马变换、对数增强）和直方图修正等。
邻域增强算法分为图像平滑和锐化两种。平滑常用算法有均值滤波、中值滤波。锐化常用算法有梯度法（如Roberts梯度法）、算子法（Sobel算子和拉普拉斯算子等）、掩模匹配法、统计差值法等。

（1）点运算算法

from skimage import exposure

def image_gamma_transform(pil_im, gamma):
    '''
    伽马变换
    INPUT  -> 单张图文件
    OUTPUT -> 处理后的图文件
    '''
    image_arr = np.array(pil_im)
    image_arr2 = exposure.adjust_gamma(image_arr, gamma)
    return array_to_image(image_arr2)

def image_gamma_transform2(pil_im, gamma):
    '''
    伽马变换2（源码实现）
    INPUT  -> 单张图文件
    OUTPUT -> 处理后的图文件
    '''
    image_arr = np.array(pil_im)
    image_arr2 = np.power(image_arr / float(np.max(image_arr)), gamma)
    return array_to_image(image_arr2*float(np.max(image_arr)))

def image_log_transform(pil_im):
    '''
    图像对数增强
    INPUT  -> 单张图文件
    OUTPUT -> 处理后的图文件
    '''
    image_arr = image_to_array(pil_im)
    if len(image_arr.shape) == 3:
        for i in range(3):
            image_arr[:,:,i] = 255/np.log(255+1)*np.log(1+image_arr[:,:,i])
        return array_to_image(image_arr)
    elif len(image_arr.shape) == 2:
        # image_arr = 255/np.log(np.max(image_arr)+1)*np.log(1+image_arr)
        image_arr = 255/np.log(255+1)*np.log(1+image_arr)
        return array_to_image(image_arr)

def image_histeq(pil_im):
    '''
    直方图均衡化
    INPUT  -> 单张图文件
    OUTPUT -> 处理后的图文件
    '''
    # 计算图像的直方图
    image_arr = image_to_array(pil_im)
    imhist, bins = np.histogram(image_arr.flatten(), 256, normed=True)
    cdf = imhist.cumsum()   # 累计分布函数
    cdf = 255*cdf/cdf[-1]   # 归一化
    # 使用累计分布函数的线性插值计算新的像素值
    image_arr2 = np.interp(image_arr.flatten(), bins[:-1], cdf)
    return array_to_image(image_arr2.reshape(image_arr.shape))

（2）邻域增强算法之平滑

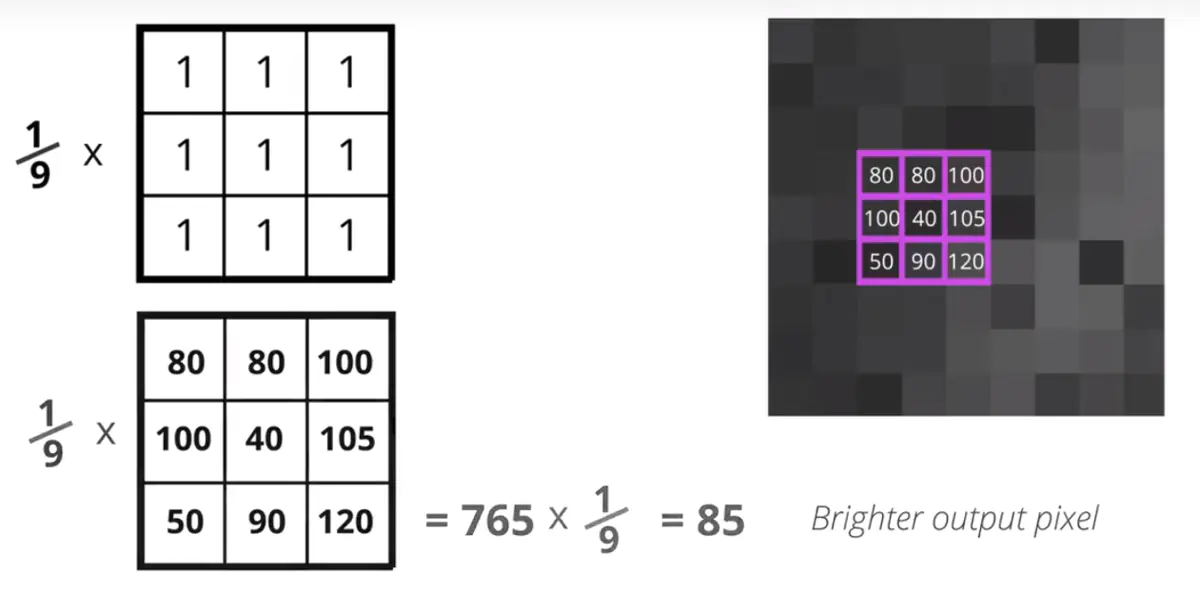
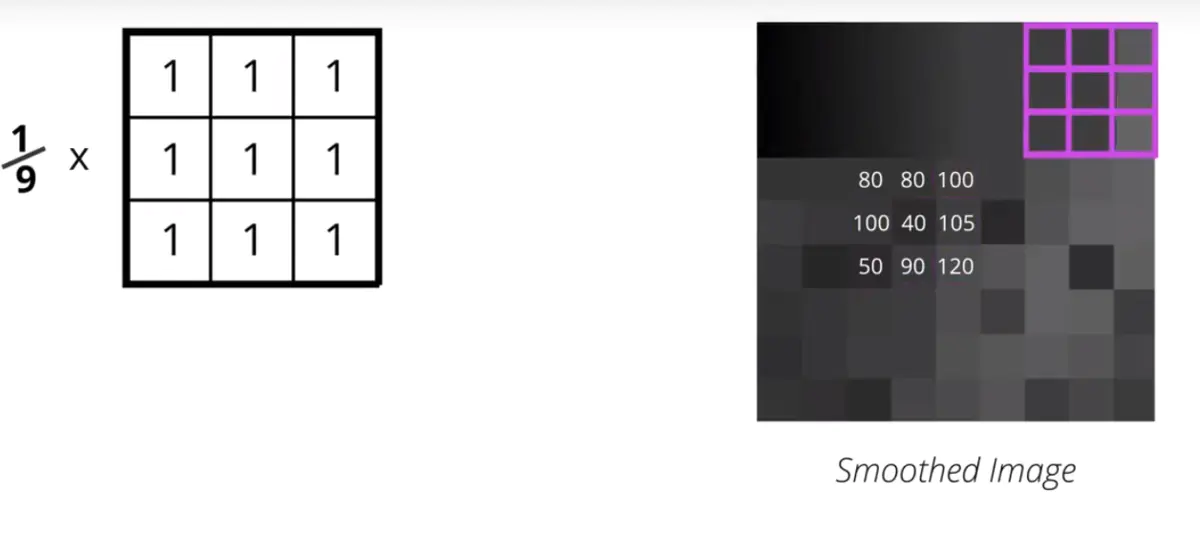
均值滤波

也称线性滤波，主要采用邻域平均法。

均值滤波的核心思想是其将整个图像看成是由很多灰度恒定的小块组成，相邻像素间相关性很强（任意一点的像素值，都是周围N*M个像素值的均值），但噪声具有统计独立性。通过均值滤波减少了灰度的突变。

均值滤波可以加上两个参数，即迭代次数，Kernel数据大小。一个相同的Kernel，但是多次迭代就会效果越来越好。同样，迭代次数相同，Kernel矩阵越大，均值滤波的效果就越明显。

from scipy.signal import convolve2d

def image_mean_filter(pil_im):
    '''
    均值滤波
    INPUT  -> 单张图文件
    OUTPUT -> 处理后的图文件
    '''
    image_arr = image_to_array(pil_im)
    dst_arr = np.zeros_like(image_arr)
    # 卷积核-均值算子
    mean_operator = np.array([[1, 1, 1], 
                            [1, 1, 1], 
                            [1, 1, 1]])/9
    if len(image_arr.shape) == 3:
        for i in range(3):
            dst_arr[:,:,i] = convolve2d(image_arr[:,:,i], mean_operator, mode="same")
    elif len(image_arr.shape) == 2:
        dst_arr = convolve2d(image_arr, mean_operator, mode="same")
    
    return array_to_image(dst_arr)

中值滤波

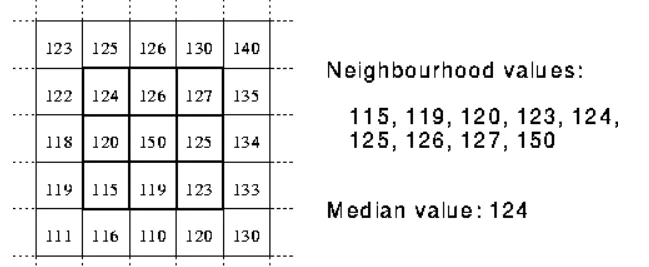
中值滤波也是消除图像噪声最常见的手段之一，特别是消除椒盐噪声，中值滤波的效果要比均值滤波更好。中值滤波是跟均值滤波唯一不同是，不是用均值来替换中心每个像素，而是将周围像素和中心像素排序以后，取中值。

from scipy.ndimage import filters

def image_medium_filter(image_arr, K=5):
    '''
    中值滤波
    中值平滑只对特别尖锐的信号平滑
    INPUT  -> 图像数组
    OUTPUT -> 去噪后的图像数组
    '''
    if len(image_arr.shape) == 3:
        for i in range(3):
           image_arr[:,:,i] = filters.median_filter(image_arr[:,:,i], K)
        return image_arr   
    elif len(image_arr.shape) == 2:
        image_arr = filters.medianBlur(image_arr, K)
        return image_arr

（3）邻域增强算法之锐化

from scipy.signal import convolve2d

def image_laplace_filter(pil_im):
    '''
    拉普拉斯算子增强
    INPUT  -> 单张图文件
    OUTPUT -> 处理后的图文件
    '''
    image_arr = np.array(pil_im)
    dst_arr = np.zeros_like(image_arr)
    filter_arr = dst_arr
    # 卷积核-拉普拉斯算子
    laplace_operator = np.array([[0, -1, 0], 
                                [-1, 4, -1], 
                                [0, -1, 0]])
    if len(image_arr.shape) == 3:
        for i in range(3):
            dst_arr[:,:,i] = convolve2d(image_arr[:,:,i], laplace_operator, mode="same")
            filter_arr[:,:,i] = image_Gaussian_filter(dst_arr[:,:,i], 5)
    elif len(image_arr.shape) == 2:
        dst_arr = convolve2d(image_arr, laplace_operator, mode="same")
        filter_arr = image_Gaussian_filter(dst_arr, 5)
    dst_arr = image_arr + filter_arr
    dst_arr = dst_arr / 255.0
    # 饱和处理
    mask_1 = dst_arr  < 0 
    mask_2 = dst_arr  > 1
    dst_arr = dst_arr * (1-mask_1)
    dst_arr = dst_arr * (1-mask_2) + mask_2
    return array_to_image(dst_arr*255)