求解等式条件极值——简单理解拉格朗日乘数法
在测量平差中,我们知道平差的准则是 V T P T = m i n V^TPT=min VTPT=min,间接平差中,我们的目标依然是 V T P T = m i n V^TPT=min VTPT=min,但在附有限制条件的间接平差中,我们的目标却是 V T P V + 2 K s T ( C x ^ − W x ) = m i n V^TPV+2K_s^T(C\hat{x}−W_x)=min VTPV+2KsT(Cx^−Wx)=min。那么这个后面加上的 2 K s T ( C x ^ − W x ) 2K_s^T(C\hat{x}−W_x) 2KsT(Cx^−Wx)是什么呢?为什么要加上呢。这就要从说起拉格朗日乘数法
先举个例子
已知 4 x 2 + y 2 + x y = 1 4x^2+y^2+xy=1 4x2+y2+xy=1,求 2 x + y 2x+y 2x+y的最大值
这就是一个求极值的问题,但是是在某一个条件下。我们最容易想到的是换元法、消元法等。但在这里我们就可以用到一个新的方法——拉格朗日乘数法
先就这个问题来看, f ( x ) = 2 x + y f(x)=2x+y f(x)=2x+y是我们的目标函数, g ( x ) = 4 x 2 + y 2 + x y − 1 = 0 g(x)=4x^2+y^2+xy-1=0 g(x)=4x2+y2+xy−1=0是我们的条件函数,那么我们就可以构造拉格朗日函数
L ( x , y , λ ) = f ( x , y ) + λ g ( x , y ) L(x,y,λ)=f(x,y)+λg(x,y) L(x,y,λ)=f(x,y)+λg(x,y)
= 2 x + y + λ ( 4 x 2 + y 2 + x y − 1 ) \qquad\qquad\ =2x+y+λ(4x^2+y^2+xy-1) =2x+y+λ(4x2+y2+xy−1)
由于 g ( x ) = 0 g(x)=0 g(x)=0,所以 L ( x , y , λ ) L(x,y,λ) L(x,y,λ)和 f ( x , y ) f(x,y) f(x,y)就是一样的,求 f ( x , y ) f(x,y) f(x,y)的最大值,就是求 L ( x , y , λ ) L(x,y,λ) L(x,y,λ)的最大值
在没有条件的求极值的时候,通常是对每个变量求偏导,然后使得每个偏导同时为零,得到驻点,再进行判断。这里的 L ( x , y , λ ) L(x,y,λ) L(x,y,λ)已经算一个没有约束的目标了,所以对各个变量求偏导并使其为零
L x ′ ( x , y , λ ) = f x ′ ( x , y ) + λ g x ′ ( x , y ) ⋅ ⋅ ⋅ ① L'_x(x,y,λ)=f'_x(x,y)+λg'_x(x,y)···① Lx′(x,y,λ)=fx′(x,y)+λgx′(x,y)⋅⋅⋅①
L y ′ ( x , y , λ ) = f y ′ ( x , y ) + λ g y ′ ( x , y ) ⋅ ⋅ ⋅ ② L'_y(x,y,λ)=f'_y(x,y)+λg'_y(x,y)···② Ly′(x,y,λ)=fy′(x,y)+λgy′(x,y)⋅⋅⋅②
L λ ′ ( x , y , λ ) = g ( x , y ) = 0 ⋅ ⋅ ⋅ ③ L'_λ(x,y,λ)=g(x,y)=0···③ Lλ′(x,y,λ)=g(x,y)=0⋅⋅⋅③
由①②得到④
f x ′ ( x , y ) g x ′ ( x , y ) = f y ′ ( x , y ) g y ′ ( x , y ) ⋅ ⋅ ⋅ ④ \frac{f'_x(x,y)}{g'_x(x,y)}=\frac{f'_y(x,y)}{g'_y(x,y)}···④ gx′(x,y)fx′(x,y)=gy′(x,y)fy′(x,y)⋅⋅⋅④
计算得到 y = 2 x y=2x y=2x,代入③中得到 x = ± 10 10 , y = ± 10 5 x=±\frac{\sqrt{10}}{10},y=±\frac{\sqrt{10}}{5} x=±1010,y=±510,所以 f ( x ) m a x = 2 10 5 f(x)_{max}=\frac{2\sqrt{10}}{5} f(x)max=5210
现在我们解决了这个题,我们就可以回到开头,回答间接平差的目标是 V T P V = m i n V^TPV=min VTPV=min,而附有参数的间接平差的目标是 V T P V + 2 K s T ( C x ^ − W x ) = m i n V^TPV+2K_s^T(C\hat{x}−W_x)=min VTPV+2KsT(Cx^−Wx)=min。我们看看附有参数的间接平差的基础方程
v = B x ^ − l 误 差 方 程 v = B\hat{x} - l {\qquad\qquad误差方程} v=Bx^−l误差方程
C x ^ − W x = 0 条 件 方 程 C\hat{x} - W_x = 0 {\qquad\ \ \ \ 条件方程} Cx^−Wx=0 条件方程
根据误差方程我们知道 V T P V = m i n V^TPV=min VTPV=min,也就是上面的目标函数 f ( x ) f(x) f(x),而这里的条件方程 x ^ − W x = 0 \hat{x}-W_x=0 x^−Wx=0就是间接平差的约束条件,也就是上面的条件函数 g ( x ) g(x) g(x),那么就有
L ( x , y , λ ) = f ( x ) + λ g ( x ) = V T P V + λ ( C x ^ − W x ) L(x,y,λ)=f(x)+λg(x)=V^TPV+λ(C\hat{x}−W_x) L(x,y,λ)=f(x)+λg(x)=VTPV+λ(Cx^−Wx)
这里的 λ λ λ换成 2 K s T 2K_s^T 2KsT,就得到了
L ( x , y , λ ) = f ( x ) + λ g ( x ) = V T P V + 2 K s T ( C x ^ − W x ) L(x,y,λ)=f(x)+λg(x)=V^TPV+2K_s^T(C\hat{x}−W_x) L(x,y,λ)=f(x)+λg(x)=VTPV+2KsT(Cx^−Wx)
式中 K s T K^T_s KsT是拉格朗日乘子,前面系数 2 2 2是为了让结果更简洁
现在我们知道了怎么用拉格朗日乘数法计算条件极值的问题。注意拉格朗日乘数法得到的结果是可能的极值点(偏导存在的极值点),是极大值极小值或者没有极值的情况,需要根据题目和函数判断
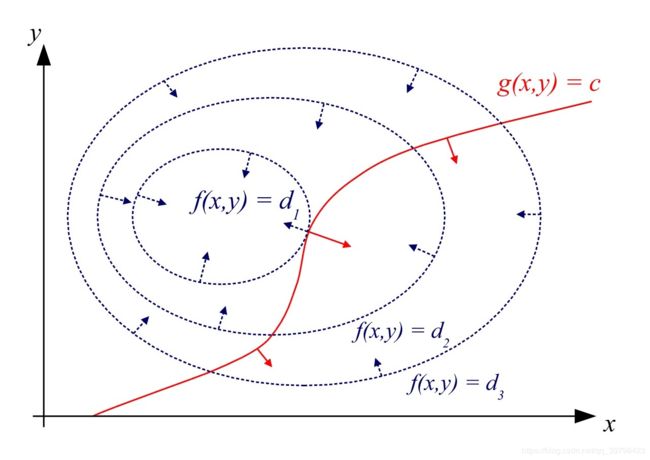
那么为什么这样可以得到约束下的极值。下面的图中蓝色的虚线是 f ( x , y ) = p f(x,y)=p f(x,y)=p的图像,红色的是约束条件 g ( x ) g(x) g(x)的图像
(图源:https://en.wikipedia.org/wiki/Lagrange_multiplier)
如我们要在图中找到一个极值,也就是这个 d 1 d_1 d1,我们可以发现 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)相切了。如果蓝色的圈还小于 d 1 d_1 d1,则根本没有满足约束条件 g ( x ) g(x) g(x),而当在 d 2 d_2 d2或 d 3 d_3 d3位置时如果是极值,那么沿着红线移动又会与其他的 d i d_i di相交,所以 d 2 d_2 d2或 d 3 d_3 d3一定不是极值点。所以就得到了极值点 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)相切。就意味着两个函数的法线在切点重合,也就是两个函数的法向量相差一个系数 λ λ λ,就得到 ( f x ′ , f y ′ ) = λ ( g x ′ , g y ′ ) (f'_x,f'_y)=λ(g'_x,g'_y) (fx′,fy′)=λ(gx′,gy′),也就是拉格朗日乘数法的几何上的理解
拉格朗日乘数法的推广
目标函数:
f ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) f(x_1,x_2,x_3···x_n) f(x1,x2,x3⋅⋅⋅xn)
约束条件:
g 1 ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) g_1(x_1,x_2,x_3···x_n) g1(x1,x2,x3⋅⋅⋅xn)
g 2 ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) g_2(x_1,x_2,x_3···x_n) g2(x1,x2,x3⋅⋅⋅xn)
⋅ ⋅ ⋅ ··· ⋅⋅⋅
g n ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) g_n(x_1,x_2,x_3···x_n) gn(x1,x2,x3⋅⋅⋅xn)
拉格朗日函数:
L ( x , y , λ ) = f ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) + λ 1 g 1 ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) + λ 2 g 2 ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) + ⋅ ⋅ ⋅ + λ n g n ( x 1 , x 2 , x 3 ⋅ ⋅ ⋅ x n ) L(x,y,λ)=f(x_1,x_2,x_3···x_n)+λ_1g_1(x_1,x_2,x_3···x_n)+λ_2g_2(x_1,x_2,x_3···x_n)+···+λ_ng_n(x_1,x_2,x_3···x_n) L(x,y,λ)=f(x1,x2,x3⋅⋅⋅xn)+λ1g1(x1,x2,x3⋅⋅⋅xn)+λ2g2(x1,x2,x3⋅⋅⋅xn)+⋅⋅⋅+λngn(x1,x2,x3⋅⋅⋅xn)
令以下式子为零:
L x 1 ′ = 0 L'_{x_1}=0 Lx1′=0
L x 2 ′ = 0 L'_{x_2}=0 Lx2′=0
⋅ ⋅ ⋅ ··· ⋅⋅⋅
L x n ′ = 0 L'_{x_n}=0 Lxn′=0
L λ 1 ′ = 0 L'_{λ_1}=0 Lλ1′=0
L λ 2 ′ = 0 L'_{λ_2}=0 Lλ2′=0
⋅ ⋅ ⋅ ··· ⋅⋅⋅
L λ n ′ = 0 L'_{λ_n}=0 Lλn′=0
则满足的点就可能是极值点
参考:
https://zhuanlan.zhihu.com/p/38625079
https://liam.page/2018/10/12/Lagrange-Multiplier-Method/