数据结构----C语言八种排序算法（冒泡排序，选择排序，直接插入排序，希尔排序，快速排序，堆排序，二路归并排序，基数排序）

一、冒泡排序

思路：首先将第一个记录的关键字和第二个记录的关键字进行比较，若为逆序，则将两记录交换，然后比较第二个记录和第三个记录的关键字，依次类推，直到第n-1个记录和第n个记录的关键字比较完毕为止。此过程为第一趟冒泡排序，结果使得最大的关键字被放置到最后一个记录的位置上。

                                                                                  图一   冒泡排序示例

 代码：

#include 
#include 
#include 
#include 

typedef struct stack
{
	int *data;
	int top;
}Stack;

typedef struct Que
{
	int *data;
	int head;
	int tail;
}Que;

void Swap(int *a, int *b)
{
	int c = *a;
	*a = *b;
	*b = c;
}

// O(n^2)  O(1)  稳定
void BubbleSort(int *arr, int len)
{
	int i = 0;
	int j = 0;
	for(i=0; i arr[j+1])
			{
				Swap(&arr[j], &arr[j+1]);
			}
		}
	}
}

其中时间复杂度为O()，空间复杂度为O(n)，稳定性是不稳定的。

 稳定：如果a原本在b的前面，而a=b, 排序之后a仍然在b的前面。

不稳定：如果a原本在b的前面，a=b, 排序之后a有可能在b的后面。

时间复杂度：对排序数据的总的操作次数。

空间复杂度：指算法在计算机内执行时所需存储空间的度量。

 

二、选择排序

参考本人另一条博客内容，相关链接为https://blog.csdn.net/qq_41026740/article/details/79706790

// O(n^2)   O(1)  不稳定
void  SelectSort(int *arr, int len)
{
	int min = 0;
	for (int i = 0; i < len; ++i)
	{
		min = i;
		for (int j = i + 1; j < len; ++j)
		{
			if (arr[j] < arr[min])
			{
				min = j;
			}
		}

		if (min != i)
		{
			Swap(&arr[min], &arr[i]);
		}
	}
}

三、直接插入排序

思路：以第二个数据开始，插入到数据前已排序好的数据序列中，并使其依旧有序。（示例：扑克调牌）

                                                                            图二   直接插入排序示例

代码：

void InsertSort(int *arr, int len)
{
	int tmp = 0;  //tmp保存每次插入的数据
	for(int i=1; i=0; --j)
		{
			if(arr[j] > tmp)
			{
				arr[j+1] = arr[j];
			}
			else
			{
				break;
			}
		}
		arr[j+1] = tmp;
	}
}

时间复杂度最坏为O(), 最好为O(n); 空间复杂度为O(1), 稳定性是稳定的。

 

四、希尔排序

思路：先跨越式分组，使用直接插入排序，使每组数据有序，随着分的组越来越详细，整个数据变得越来越有序，直到分组成员只有1个时，排序完成。

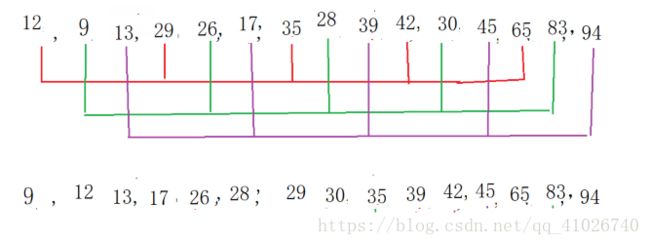
                                                图三  希尔排序示例

代码：

void Shell(int *arr, int len, int width)
{
	for (int i = width; i < len; ++i)
	{
		int tmp = arr[i];
		int j = 0;
		for (j = i - width; j >= 0; j -= width)
		{
			if (arr[j] > tmp)
			{
				arr[j + width] = arr[j];
			}
			else
			{
				break;
			}
		}

		arr[j + width] = tmp;
	}
}

//O(n^1.3) - O(n^1.5)   O(1)   不稳定
void ShellSort(int *arr, int len)
{
	int d[] = { 5, 3, 1 };  // 最后一个数据必须是1

	for (int i = 0; i < sizeof(d) / sizeof(d[0]); ++i)
	{
		Shell(arr, len, d[i]);
	}
}

 

五、快速排序

思路：每选取一个数（待排列数据的第一个数据）作为比较的基准，然后从后往前找比基准小的，将其放在前面空缺位置，其次从前往后找比基准大的数据放在后面空缺位置，直到 i 和 j 相遇。将基准放入 i 位置，基准前的数据都比基准小，基准后的数据都比基准大，然后递归分别处理左半边和右半边。

递归与非递归的区别

非递归：排序前开辟一块空间，更稳定，代码复杂，逻辑复杂；

递归：边排序边开辟空间，代码简单，逻辑简单。

// O(n)   O(1)   不稳定
int OnceQuick(int *arr, int left, int right)
{
	int i = left;
	int j = right;
	int tmp = arr[i];

	while (i < j)
	{
		// 从后往前找第一个比基准小的数据
		while (i < j && arr[j] >= tmp) j--;
		//undo
		if (i == j)
		{
			break;
		}
		arr[i] = arr[j];

		//从前往后找第一个比基准大的数据
		//undo
		while (i < j && arr[i] <= tmp) i++;
		if (i == j)
		{
			break;
		}

		arr[j] = arr[i];
	}

	arr[i] = tmp;

	return i;
}

// 递归完成  O(nlogn)   O(logn)
void Quick(int *arr, int left, int right)
{
	// 快排的一次处理过程
	int pos = OnceQuick(arr, left, right);

	if (pos - left > 1)
	{
		Quick(arr, left, pos - 1); // 递归处理基准左边的数据
	}

	if (right - pos > 1)
	{
		Quick(arr, pos + 1, right); //递归处理基准右边的数据
	}
}

// 非递归完成
void Quick2(int *arr, int left, int right)
{
	Stack st;
	int n = right - left + 1;
	int len = (int)(log10((double)n) / log10((double)2)) + 1;  // logn
	st.data = (int *)malloc(2 * sizeof(int) * len);
	assert(st.data != NULL);
	st.top = 0;

	st.data[st.top++] = left;
	st.data[st.top++] = right;

	while (st.top != 0)
	{
		right = st.data[--st.top];
		left = st.data[--st.top];

		int pos = OnceQuick(arr, left, right);

		if (right - pos > 1)
		{
			st.data[st.top++] = pos+1;
			st.data[st.top++] = right;
		}

		if (pos - left > 1)
		{
			st.data[st.top++] = left;
			st.data[st.top++] = pos - 1;
		}
	}

	free(st.data);
}

// O(nlogn)   O(logn)      不稳定
void  QuickSort(int *arr, int len)
{
	//Quick(arr, 0, len - 1);
	Quick2(arr, 0, len - 1);
}

六、堆排序

小根堆：在二叉树结构中，父节点比左右孩子都小

大根堆：在二叉树结构中，父节点比左右孩子都大

①设父节点为 i

    左孩子：2*i+1

    右孩子：2*i-1

②设孩子节点为 i

    父节点：（i-1）/2

调整到大根堆的过程：

1、整个调整过程从最后一个子树开始，依次向上调整；

2、每次调整都是从这棵子树的根节点开始往下调整。

堆排序与数据原本的顺序无关。

//O(logn)   O(1)   不稳定
void Adjust(int *arr, int len, int start)
{
	int tmp = arr[start];
	int i = start * 2 + 1;

	while (i < len)
	{
		if (i + 1 < len && arr[i + 1] > arr[i])
		{
			i += 1;
		}
		// 上一步判断完成后，则i位左右孩子较大的哪一个

		if (arr[i] < tmp)
		{
			break;
		}

		arr[start] = arr[i];
		start = i;
		i = 2 * start + 1;
	}

	arr[start] = tmp;
}

//O(nlogn)   O(1)
void CreateHeap(int *arr, int len)
{
	for (int i = (len - 2) / 2; i >= 0; --i)
	{
		Adjust(arr, len, i);
	}
}

// O(nlogn)   O(1)   不稳定
void HeapSort(int *arr, int len)
{
	CreateHeap(arr, len);

	int end = len - 1;
	while (end > 0)
	{
		Swap(&arr[0], &arr[end]);
		Adjust(arr, end, 0);
		end--;
	}
}

七、二路归并

// 二路归并  O(n)  O(n)   稳定 
void Meger(int *arr, int len, int width)
{
	int low1 = 0;
	int high1 = low1 + width - 1; // -1使得high1为本段最后一个元素的下标
	int low2 = high1 + 1;
	int high2 = low2 + width - 1 < len - 1 ? low2 + width - 1 : len - 1;

	int *brr = (int *)malloc(sizeof(int) * len);
	assert(brr != NULL);

	int index = 0;
	while (low1 < len)  //只要有一个段还没合并进brr中，循环都得执行
	{
		//按顺序归并两个相邻的段， 退出时，有可能第一个段数据归并完成
		//也有可能是第二个段数据归并完成
		while (low1 <= high1 && low2 <= high2)
		{
			if (arr[low1] < arr[low2])
			{
				brr[index++] = arr[low1++];
			}
			else
			{
				brr[index++] = arr[low2++];
			}
		}

		//将第一个段剩余的数据存储到brr中
		while (low1 <= high1)
		{
			brr[index++] = arr[low1++];
		}
		//将第二个段剩余的数据存储到brr中
		while (low2 <= high2)
		{
			brr[index++] = arr[low2++];
		}

		// 继续往后归并剩余的段
		low1 = high2 + 1;
		high1 = low1 + width - 1 < len - 1 ? low1 + width - 1 : len - 1;
		low2 = high1 + 1;
		high2 = low2 + width - 1 < len - 1 ? low2 + width - 1 : len - 1;
	}

	for (int i = 0; i < len; ++i)
	{
		arr[i] = brr[i];
	}

	free(brr);
}

//  O(nlogn)  O(n)    稳定
void MegerSort(int *arr, int len)
{
	for (int i = 1; i < len; i *= 2)
	{
		Meger(arr, len, i);
	}
}

八、基数排序

八种排序算法中，唯一不需要数据比较的算法。

出现多个关键字可以用此排序算法。

条件：数据必须全为正整数。

思路：1、找到其中最大的数据，求位数；

           2、再循环根据相应位数的值将数据放入对应的队列中；

          3、按照队列顺序将队列中的所有数据输出。

//O(n)
int GetWidth(int *arr, int len)
{
	int max = arr[0];
	for (int i = 1; i < len; ++i)
	{
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}

	// 根据max求位数   1234   234
	int width = 0;
	while (max > 0)
	{
		width += 1;
		max /= 10;
	}

	return width;
}

//  1234
// O(d)
int GetRadixVal(int val, int digit) // val = 1234 digit = 0
{
	while (digit > 0)
	{
		val /= 10;
		digit--;
	}

	return val % 10;
}

//O(dn)   O(n)   稳定
void RadixSort(int *arr, int len)
{
	Que que[10];
	for (int i = 0; i < 10; ++i)
	{
		que[i].data = (int *)malloc(sizeof(int)* len);
		assert(que[i].data != NULL);
		que[i].head = que[i].tail = 0;
	}
	int width = GetWidth(arr, len);

	for (int i = 0; i < width; ++i)
	{
		for (int j = 0; j < len; j++)
		{
			int digitval = GetRadixVal(arr[j], i);
			que[digitval].data[que[digitval].tail++] = arr[j];
		}	

		int count = 0;
		for (int k = 0; k < 10; ++k)
		{
			while (que[k].head != que[k].tail)
			{
				arr[count++] = que[k].data[que[k].head++];
			}

			que[k].head = que[k].tail = 0;
		}
	}

	for (int i = 0; i < 10; ++i)
	{
		free(que[i].data);
	}
}

//输出函数
void Show(int arr[], int len)
{
	for (int i = 0; i < len; ++i)
	{
		printf("%d  ", arr[i]);
	}

	printf("\n");
}

主函数的测试代码：

int main()
{
	int arr[] = {35,26,13,228,65,45,139,42,717,239,83, 123,563,1276};

	int len = sizeof(arr) / sizeof(arr[0]);

	//BubbleSort(arr, len);冒泡排序
	//SelectSort(arr, len);选择排序
	//QuickSort(arr, len);快速排序
	//HeapSort(arr, len);堆排序
	//MegerSort(arr, len);二路归并排序
	RadixSort(arr, len);//基数排序
	Show(arr, len);

}