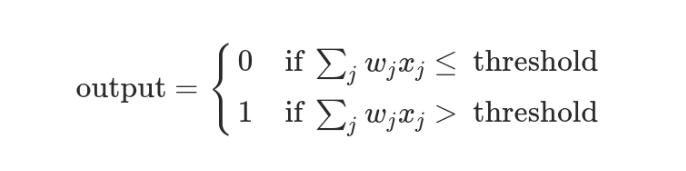机器学习笔记-人工神经网络（artificial neural networks）

目录

人工神经网络（ANN）

引言

感知器

什么是感知器？

感知器的例子

权重和阈值

多层前馈神经网络

网络结构

正向传播

反向传播（Error Back Propagation，BP算法）

​

后话：深度学习、神经网络、机器学习、人工智能的关系

深度学习、机器学习、人工智能

深度学习、神经网络

reference

---

人工神经网络（ANN）

引言

人的大脑由大约 800 亿个神经元组成，每个神经元通过突触与其他神经元相连接，接收这些神经元传来的电信号和化学信号，对信号汇总处理之后输出到其他神经元。大脑通过神经元之间的协作来完成它的功能，神经元之间的连接关系是在进化过程中以及生长发育、长期的学习、对外界环境的剌激反馈中建立起来的。
人工神经网络是对这种机制的简单模拟 它由多个相互连接的神经元构成，这些神经元从其他相连的神经元接收输入数据’，通过计算产生输出数据，这些输 出数据可能会送入其 神经元继续处理。
       人工神经网络应用广泛。除了用于模式识别之外，它还可以用于求解函数的极值、自动控制等问题 到目前为止有 种不同结构的神经网络，典型的有多层前馈型神经网络（可称为全连接神经网络）、卷积神经网络（CNN)、循环神经网络（RNN）等。
       神经网络是一种很古老的算法，它最初产生的目的是制造能模拟大脑的机器。神经网络逐渐兴起于二十世纪八九十年代，应用得非常广泛。但由于各种原因，在 90年代的后期应用减少了（期间SVM流行）。但是最近，神经网络又东山再起了。其中一个原因是：神经网络是计算量有些偏大的算法。然而大概由于近些年计算机的运行速度变快，才足以真正运行起大规模的神经网络。正是由于这个原因和其他一些我们后面会讨论到的技术因素，如今的神经网络对于许多应用来说是最先进的技术。

感知器

什么是感知器？

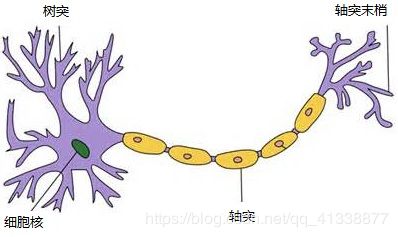
历史上，科学家一直希望模拟人的大脑，造出可以思考的机器。人为什么能够思考？科学家发现，原因在于人体的神经网络。 

                                                                典型的神经元结构示意图
1、外部刺激通过神经末梢，转化为电信号，转导到神经细胞（又叫神经元）。
2、无数神经元构成神经中枢。
3、神经中枢综合各种信号，做出判断。
4、人体根据神经中枢的指令，对外部刺激做出反应。

既然思考的基础是神经元，如果能够"人造神经元"（artificial neuron），就能组成人工神经网络，模拟思考。上个世纪六十年代，提出了最早的"人造神经元"模型，叫做"感知器"（perceptron），直到今天还在用。                             

                                                                          M-P神经元模型
上图的圆圈就代表一个感知器。它接受多个输入（x1，x2，x3...），产生一个输出（output），好比神经末梢感受各种外部环境的变化，最后产生电信号。

为了简化模型，我们约定每种输入只有两种可能：1 或 0。如果所有输入都是1，表示各种条件都成立，输出就是1；如果所有输入都是0，表示条件都不成立，输出就是0。

感知器的例子

下面来看一个例子。大山准备周末去杭州乐园玩，但是还拿不定主意。
他决定考虑三个因素。

1、天气(x1）：周末是否晴天？
2、同伴(x2)：能否找到人一起去？
3、价格(x3)：门票是否可承受？1

这就构成一个感知器。上面三个因素就是外部输入，最后的决定就是感知器的输出。如果三个因素都是 Yes（使用1表示），输出就是1（去参观）；如果都是 No（使用0表示），输出就是0（不去参观）。

权重和阈值

看到这里，你肯定会问：如果某些因素成立，另一些因素不成立，输出是什么？比如，周末是好天气，门票也不贵，但是大山找不到同伴，他还要不要去参观呢？

现实中，各种因素很少具有同等重要性：某些因素是决定性因素，另一些因素是次要因素。因此，可以给这些因素指定权重（weight），代表它们不同的重要性。

• 天气：权重为8
• 同伴：权重为4
• 价格：权重为4

上面的权重表示，天气是决定性因素，同伴和价格都是次要因素。

如果三个因素都为1，它们乘以权重的总和就是 8 + 4 + 4 = 16。如果天气和价格因素为1，同伴因素为0，总和就变为 8 + 0 + 4 = 12。

这时，还需要指定一个阈值（threshold）。如果总和大于阈值，感知器输出1，否则输出0。假定阈值为8，那么 12 > 8，小明决定去参观。阈值的高低代表了意愿的强烈，阈值越低就表示越想去，越高就越不想去。

上面的决策过程，使用数学表达如下。

上面公式中，x表示各种外部因素，w表示对应的权重。

多层前馈神经网络

网络结构

用于分类题时，神网络一般有多个层 。第一层为输入层，对应输入向量，神经元的数量等于特征向量的维数，这个层不对数据进行处理，只是将输入向量传入下一层中进行计算。中间为隐含层，可能很多层（通常将除输入层、输出层之外的神经网络层都视为隐含层），最后一层是输出层，神经元的数量等于要分类的类别数，输入层的输入值用来做分类预测。

举个栗子！

                                               

                                                                                 一个简单的神经网络

由三层网络构成：

1. 第一层：输入层（input）对应输入向量x,有3个神经元，写成分向量形式即（x1,x2,x3），它们对数据不进行任何处理，直接送到下一层。
2. 第二层：隐含层（hidden）有4个神经元，接受数据为x,输出向量为y=（y1,y2,y3,y4）
3. 第三层：输出层（output）接受数据为y,输出向量为z=（z1,z2)

第一层到第二层的权重矩阵为 ，第二层到第三层的权重矩阵为 。权重矩阵的每一行为一个权重向量 ，是上一层所有神经元到本层某一个神经元的连接权重，这里的上标表示层数。

正向传播

下面把这个简单的例子推广到更一般的情况。假设神经网络的输入是n维向量x ，输出是m维向量y 。

它实现了如下向量到向量的映射：

x=(x1,x2,...,xn)

y=(y1,x2,...,ym)

把这函数记为

用于分类问题时，比较输出向量y中每个分量y1,x2,...,ym的大小，求其最大值，最大值对应的分量下标即为分类的结果。用于回归问题时，直接将输出向量作为回归值。

神经网络第i层的变换写成矩阵和向量形式为：

为前一层（第 i- 1层）的输出向量，也是本层接收的输入向量；

为本层神经元和上一层神经元的连接权重矩阵，是一个 的矩阵，其中,为本层神经元数, 为前 一层神经元数量，的每个行为本层 个神经元与上一层所有神经元的权 重向量；

为本层的偏置向量，是一个 维的列向量；

激活函数f(x)分别作用于输入向量的每一个分量，产生一个向量输出。

在计算网络输出值的时候，从输入层开始，对于每层都用上面的两个公式进行计算， 最后得到神经网络的输出，这个过程称为正向传播，用于神经网络的预测阶段，以及训练时的正向传播阶段。

下面给出正向传播算法的流程。假设神经网络有m层，第一层为输入层，输入向量为x ，第i层的权重矩阵为 偏置向量为 。

正向传播算法的流程为：

设置

循环 i=2,3 ，…，m，对每

计算

计算

结束循环

输出向量 ，作为神经网络的预测值

前向传播理解起来并不难，就是把前一层的输出作为下一层的输入，循环，直到最后一层的输出层。大家应该疑惑那么每层间的权重矩阵、偏置向量、激活函数阈值是何如确定的？

神经网络的学习过程，就是根据训练数据来调整神经元之间的“连接权”、偏置值以及每个功能神经元的阈值；换而言之，神经网络“学”到的东西就蕴含在这三种参数之中。

回答了学什么，那是怎么学？往下看

反向传播（Error Back Propagation，BP算法）

PS：我认为BP算法是神经网络最难啃的一块骨头，不过，也得啃下它。如今大佬博客如此之多，总能找到几个解释得好的教程，我拿过来消化融合成自己易懂的便是。

• 核心问题：解决神经网络参数求导问题
• 源自多元函数的链式法则（链式法则：17世纪）
• 与梯度下降法配合，完成网络的训练

bp算法历史概述：1986，Nature

深度学习之父Hinton

可能你还觉得BP算法太玄乎了，我们还举上面三层网络来说。

前面我说过了：前向传播神经网络每层的权重矩阵、偏置向量、激活函数阈值我们是不知道的，它们是我们要“学习”得到的东东（即参数）。在应用时，它们初始化的值往往是随机赋予的，所以说，我们使用前向传播进行预测值就会和真实值有偏差，而BP算法就是去纠正这个偏差的！那如何纠正纠偏差？答案：Back Propagation（BP算法）。

BP算法推导内容较多，故放到专门的一篇文章中（点我）。

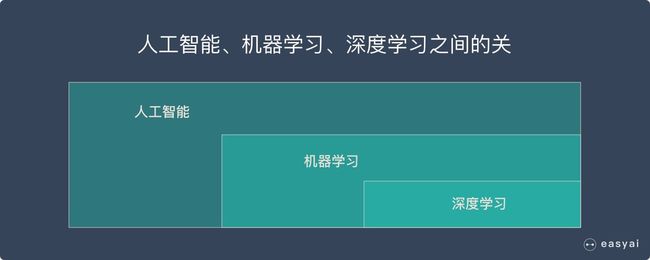
后话：深度学习、神经网络、机器学习、人工智能的关系

• 深度学习、机器学习、人工智能

简单来说：

1. 深度学习是机器学习的一个分支(最重要的分支)
2. 机器学习是人工智能的一个分支

   

• 深度学习、神经网络

深度学习的概念源于人工神经网络的研究，但是并不完全等于传统神经网络。

不过在叫法上，很多深度学习算法中都会包含”神经网络”这个词，比如：卷积神经网络、循环神经网络。

所以，深度学习可以说是在传统神经网络基础上的升级，约等于神经网络。

 

reference

机器学习与应用（雷明）第九章

机器学习（周志华）      第五章

吴恩达老师机器学习个人笔记完整版

深度学习 – Deep learning | DL