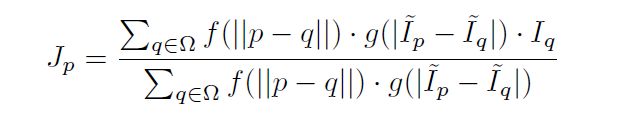计算机视觉实验二:图像滤波处理——高斯滤波和联合双边滤波
完整源码链接 https://github.com/LamyaLi/cvLab
一、 图像的高斯滤波处理
文章目录
- 一、 **图像的高斯滤波处理**
- 1、题目要求
- 2、题目分析
- 3、实现步骤(仅展示部分关键代码)
- 4、结果展示
- 二、 **图像的联合双边滤波处理**
- 1、题目要求
- 2、题目分析
- 3、实现步骤(仅展示部分关键代码)
- 4、结果展示
1、题目要求
1)通过调整高斯函数的标准差(sigma)来控制平滑程度;
给定函数:void Gaussian(const MyImage &input, MyImage &output, double sigma);
2)滤波窗口大小取为[6* sigma-1]/2* 2+1,[.]表示取整;
3)利用二维高斯函数的行列可分离性进行加速;
先对每行进行一维高斯滤波,再对结果的每列进行同样的一维高斯滤波;
空间滤波=图像卷积;
高斯滤波=以高斯函数为卷积核的图像卷积。
2、题目分析
-
高斯滤波是一种线性平滑滤波,适用于消除高斯噪声,广泛应用于图像处理的减噪过程。 [1] 通俗的讲,高斯滤波就是对整幅图像进行[加权平均]的过程,每一个像素点的值,都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是:用一个模板(或称卷积、掩模)扫描图像中的每一个像素,用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
-
滤波窗口大小取为[6* sigma-1]/2* 2+1,其中/代表整除,下去整,这个式子保证size是奇数
-
滤波窗口大小选取,是基于,高斯分布距离均值3*sigma以外的点的概率密度很低,可以忽略的原理
-
高斯滤波窗口是可行列分离窗口,由于对称性,分离出的行和列,取值是一样的;且先对图像用行的核遍历卷积一遍得到中间图像,再对中间图像用列的核遍历卷积一遍,得到的结果图,与直接对原图用完整核,效果一样。由于行列分离可以减少计算量,所以实现一定程度的加速
-
对图像进行滤波处理,需要考虑边界问题。本实验将采用valid的方式,即边界保留原图像的取值
3、实现步骤(仅展示部分关键代码)
1)生成高斯核,由于采用行列分离,这里仅需利用一维高斯分布概率密度函数,生成(size,1)大小的核
def getGaussianCore(sigma):
size = int(sigma * 6 - 1) // 2 * 2 + 1
centre=size//2
core= np.zeros([size], np.float32)
coefficient=1.0/(sigma*((2*math.pi)**0.5))
sum=0
for i in range(size):
core[i]=coefficient*math.exp(-0.5*((i-centre)/sigma)**2)
sum=sum+core[i]
#归一化
core=core/sum
return core
2)行卷积,列卷积,得到结果图并显示,只放了行卷积代码
def Gaussian(img_input,img_output,sigma):
#导入图像
#Boundary是valid方式
core=getGaussianCore(sigma)
#行卷积
for i in range(img_size[0]):
for j in range(centre,img_size[1]-centre):
for d in range(3):
sum=0
for k in range(size):
sum=sum+core[k]*img_input[i][j-centre+k][d]
img_input2[i][j][d]=sum
#列卷积
#按img_out路径保存图片,并显示两张前后对比图
4、结果展示
sigma=1时,size=5
sigma=3时,size=17 核的大小,对时间,去噪效果有很大影响
所以,sigma取值是时间,去噪效果,模糊效果多种因素的权衡
二、 图像的联合双边滤波处理
1、题目要求
给定函数:function im = jbf(D,C,w, sigma_f, sigma_g)
其中:D为输入图像;C为引导图像;W为滤波窗口大小;
sigma_f 为spatial kernel标准差;sigma_g为range kernel 标准差;
给定公式:
其中:q是p的邻域中的一个像素。 f和g是空间和距离内核,通常以高斯的形式表示,I是输入图像。
f 是空间滤波器内核,定义为:exp([-d_f2]/[2*sigma_f2])
其中:d_f 为输入图像I的像素位置差,sigma_f为空间滤波核函数的标准差
g是距离滤波器内核,定义为:exp([-d_g2]/[2*sigma_g2])
其中:d_g为引导图像 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NKyRz7yS-1579076000177)(file:///C:/Users/12407/AppData/Local/Temp/msohtmlclip1/01/clip_image008.png)]的像素灰度值差,sigma_g为滤波核函数的标准差
输入图像I下采样(1/2)得到LR低分辨率图像,再由LR图像上采样2倍得到引导图像。
注:图像缩放采用双线性插值。
2、题目分析
- 双边滤波(Bilateral filter)是一种非线性的滤波方法,是结合图像的空间邻近度和像素值相似度的一种折中处理,同时考虑空域信息和灰度相似性,达到保边去噪的目的。
双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma-d,它是基于空间分布的高斯滤波函数,所以在边缘附近,离的较远的像素不会太多影响到边缘上的像素值,这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息,对于彩色图像里的高频噪声,双边滤波器不能够干净的滤掉,只能够对于低频信息进行较好的滤波。
双边滤波器的权值不够稳定,而联合双边滤波器就是在双边滤波器的基础上引入了引导图像,使得权值更稳定。
-
引导图像需要用到双线性插值,由于,实验三将详细解释双线性插值,这里不再展开说明
-
边界问题。本实验将采用valid的方式,即边界保留原图像的取值
3、实现步骤(仅展示部分关键代码)
1)提前计算好一个距离核
def jbf(source,guide,size,sigma_f,sigma_g):
starttime=datetime.datetime.now()
# 联合双边滤波
# source为输入图像,三维矩阵
# guide为引导图像,三维矩阵
# size为滤波窗口大小
# sigma_f为spatial kernel标准差
# sigma_g为range kernel 标准差
#返回处理后的图像的三维矩阵
# Boundary是valid方式
des=source.copy()
distance = np.zeros([size, size], dtype=np.uint8)
for m in range(size):
for n in range(size):
distance[m, n] = (m - size // 2) ** 2 + (n - size // 2) ** 2
2)三层for循环实现卷积遍历,实时计算原图窗口,引导图窗口,根据要求中的计算公式,算出当前(i,j,d)处的灰度值。矩阵对应元素相乘,根据numpy的广播机制直接用* 号即可,非常方便
for i in range(size//2,guide.shape[0]-size//2):
for j in range(size//2,guide.shape[1]-size//2):
for d in range(3):
#计算当前窗口范围
istart = i - size//2
iend = i+size//2
jstart = j - size//2
jend = j+size//2
#原图的当前窗口
window_s = source[istart:iend+1, jstart: jend+1, d]
#引导图的当前窗口
window_g = guide[istart:iend+1, jstart: jend+1, d]
#由引导图像的灰度值差计算值域核
g = np.exp(-0.5*(window_g - guide[i, j,d])**2 / (sigma_g **2))
f=np.exp(-0.5*distance/(sigma_f**2))
des[i,j,d]=int(np.sum(g*f*window_s)/np.sum(g*f))
endtime = datetime.datetime.now()
print('联合双边滤波操作时间:', endtime - starttime)
return des
4、结果展示





![]()
基本可以看出,size越大,时间越久,越模糊;除此之外,sigma_f和sigma_g也是重要的参数
未达到比较理想的去噪效果,size不宜过大,也不宜过小,取5;sigma_f不宜过大,否则失去其保边效果;
sigma_g应该要比sigma_f大些,使得去噪效果主导。