c++学习之根据任意三个坐标的判断三角形的类型（面积、周长）

本次介绍一下，根据输入的任意三个点坐标，判断是否可以构成三角形，以及计算周长，面积。

一、设计的构想

1.1、思路介绍

首先，来看一个坐标图（不要嫌弃）：

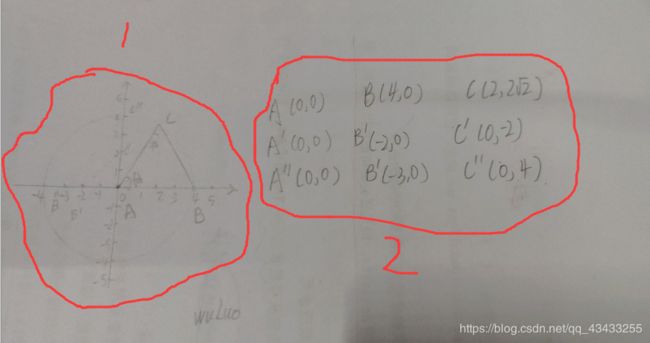
图1的部分是，一个简易坐标；图2部分是三组坐标。
1）根据输入的三个坐标，判断能否组成三角形；
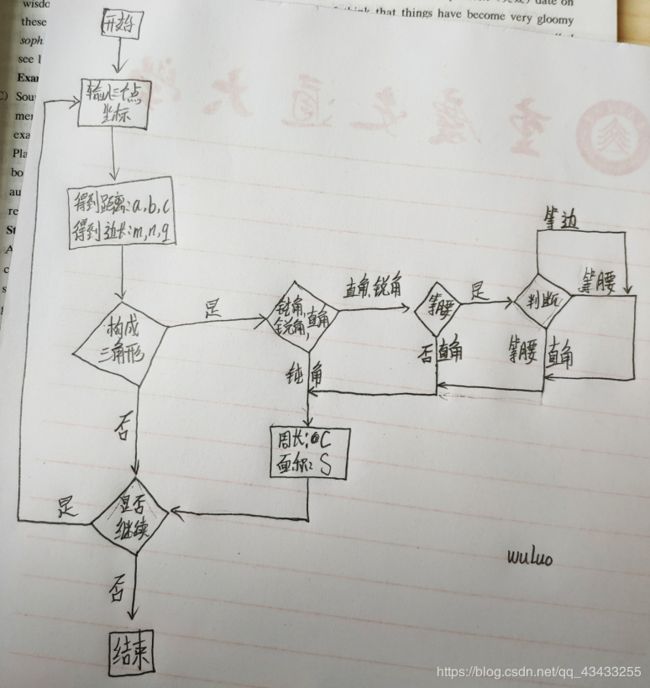
2）先将三角形分为钝角三角形、直角三角形、锐角三角形；
3）再将直角三角形与锐角三角形细分，如直角三角形、锐角三角形、等腰三角形、直角等腰三角形、等边三角形（经验证，通过坐标，最难实现），也可以说是划分等腰三角形、直角等腰三角形、等边三角形；
4）计算周长、面积；
5）判断是结束运行，还是继续。

1.2、流程图

流程画的不是很规范：

二、代码的实现

2.1、函数的介绍

根据上面的思路，来介绍各部分函数（为了方便，直接上图）。
1）判断能否组成三角形：

三角形组成的条件是：任意两边和大于第三边。
2）将三角形粗分类：

根据三角形的三条边分别的平方（a、b、c），确认最长的边之后（c)，当a与b之和大于c时，是锐角三角形;，当a与b之和与c相等时，是直角三角形；当a与b之和小于c时，是钝角三角形。
由于我定义边长是采用double，导致得到后的边长，存在平方之后得不到应有的值的情况，所以需要采用边长的平方时，我先传递原有的平方值（计算边长时，得到），这也是为什么等边三角形的坐标，最难得到，下同：

3）再将三角形细分：

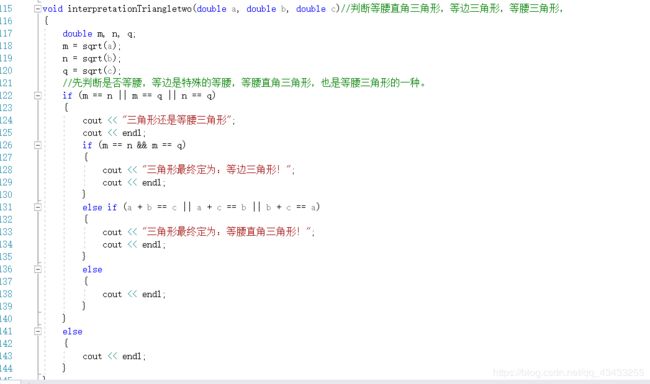
在这里，首先要明确的是等腰三角形包含（直角等腰三角形，等边三角形）。
这里需要三条边（m、n、q），与之对应边的平方和（a、b、c），根据任意两条边相等，确认为是等腰三角形；然后在根据三条边相等以及直角的判断，划分等边三角形与等腰直角三角形。
4）计算周长、面积：

周长就是三边之和，但面积有许多公式，基于设计思路，采用海伦公式。
5）循环：

这就十分简单了。根据情况，设置循环条件。

2.2、完整的代码

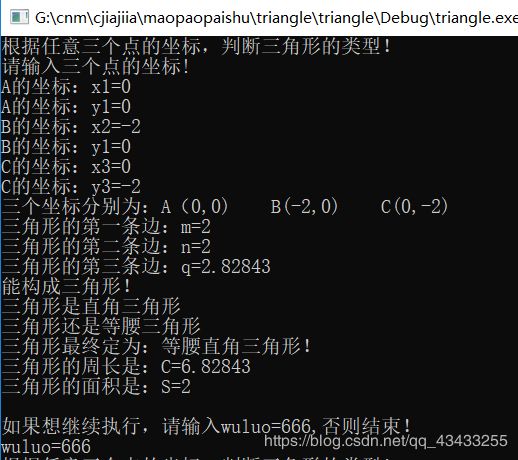
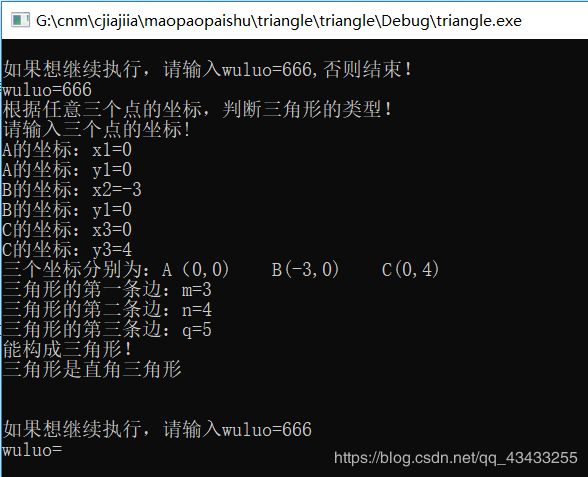
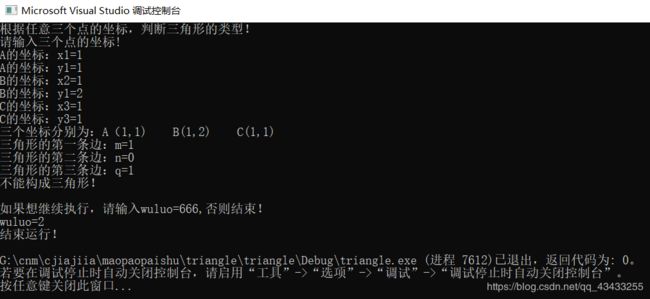
下面，就是完整的代码，另附运行情况：

// triangle.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//__author__ = 'wuluo'
//__version__ = '1.0.0'
//__company__ = u'重庆交大'
//__updated__ = '2019-05-29'

#include "pch.h"
#include 
#include 
#include
using namespace std;

void interpretationTriangle(double m,double n,double q)//判断能否构成三角形
{
 if(m+n>q&&n+q>m&&m+q>n)
 {
  cout << "能构成三角形！";
 }
 else
 {
  cout << "不能构成三角形！";
 }
 cout << endl;
}

void interpretationTriangleone(double a, double b, double c)//判断钝角三角形，锐角三角形，钝角三角形，
{
 //判断那条边最长
 if (a - b > 0 && a - c > 0)//边a最长时
 {
  
  if ( b + c> a)
  {
   cout << "三角形是锐角三角形！";
  }
  else if (a ==b  + c )
  {
   cout << "三角形是直角三角形";
  }
  else
  {
   cout << "三角形是钝角三角形";
  }
 }
 else if (b - a > 0 && b - c > 0)//边b最长时
 {
  
  if (a + c  > b)
  {
   cout << "三角形是锐角三角形！";
  }
  else if (a + c  == b )
  {
   cout << "三角形是直角三角形";
  }
  else
  {
   cout << "三角形是钝角三角形";
  }
 }
 else if (c - a > 0 && c - b > 0)//边c最长时
 {
  
  if (a + b  > c)
  {
   cout << "三角形是锐角三角形！";
  }
  else if (a + b  == c )
  {
   cout << "三角形是直角三角形";
  }
  else
  {
   cout << "三角形是钝角三角形";
  }
 }
 else
 {
  cout << endl;
 }
 cout << endl;
}

void interpretationTriangletwo(double a, double b, double c)//判断等腰直角三角形，等边三角形，等腰三角形，
{
 double m, n, q;
 m = sqrt(a);
 n = sqrt(b);
 q = sqrt(c);
 //先判断是否等腰，等边是特殊的等腰，等腰直角三角形，也是等腰三角形的一种。
 if (m == n || m == q || n == q)
 {
  cout << "三角形还是等腰三角形";
  cout << endl;
  if (m == n && m == q)
  {
   cout << "三角形最终定为：等边三角形！";
   cout << endl;
  }
  else if (a + b == c || a + c == b || b + c == a)
  {
   cout << "三角形最终定为：等腰直角三角形！";
   cout << endl;
  }
  else
  {
    cout << endl; 
  }
 }
 else
 {
  
 }
}

void interpretationTrianglethree(double m, double n, double q)//计算三角形的周长以及面积
{
 double C, S,p;
 C = m + n + q;//计算周长
 p = C / 2;
 S = sqrt(p*(p - m)*(p - n)*(p - q));//计算面积，海伦公式
 cout << "三角形的周长是：C=" << C;
 cout << endl;
 cout << "三角形的面积是：S=" << S;
 cout << endl;
}

int main()
{
 double x1, y1, x2, y2, x3, y3;
 double a, b, c, m, n, q;
 int wuluo;
 cout << "根据任意三个点的坐标，判断三角形的类型！";
 cout << endl;
 cout << "请输入三个点的坐标!";
 cout << endl;
 cout << "A的坐标：x1=";
 cin >> x1;
 cout << "A的坐标：y1=";
 cin >> y1;
 cout << "B的坐标：x2=";
 cin >> x2;
 cout << "B的坐标：y1=";
 cin >> y2;
 cout << "C的坐标：x3=";
 cin >> x3;
 cout << "C的坐标：y3=";
 cin >> y3;
 cout << "三个坐标分别为：A（" << x1 << "," << y1 << ")" << "    " << "B(" << x2 << "," << y2 << ")" << "    " << "C(" << x3 << "," << y3 << ")";
 cout << endl;
 a = (x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2);
 m = sqrt(a);
 cout << "三角形的第一条边：m=" << m;
 cout << endl;
 b = (x1 - x3)*(x1 - x3) + (y1 - y3)*(y1 - y3);
 n = sqrt(b);
 cout << "三角形的第二条边：n=" << n;
 cout << endl;
 c = (x3 - x2)*(x3 - x2) + (y3 - y2)*(y3 - y2);
 q = sqrt(c);
 cout << "三角形的第三条边：q=" << q;
 cout << endl;
 interpretationTriangle(m, n, q);  //判断能否构成三角形
 if (m + n > q&&n + q > m&&m + q > n)
 {
  interpretationTriangleone(a, b, c);//判断钝角三角形，锐角三角形，钝角三角形，
 }
 if (m + n > q&&n + q > m&&m + q > n)
 {
  interpretationTriangletwo(a, b, c);//判断等腰直角三角形，等边三角形，等腰三角形，
 }
 if (m + n > q&&n + q > m&&m + q > n)
 {
  interpretationTrianglethree(m, n, q);//计算三角形面积及周长
 }
 cout << endl;
 //设置循环结构，可以使程序多次运行！
    cout << "如果想继续执行，请输入wuluo=666,否则结束！"; 
 cout << endl;
 cout << "wuluo=";
 cin >> wuluo;
 while (wuluo==666)
 {
  main();
  interpretationTriangle(m, n, q);  //判断能否构成三角形
  if (m + n > q&&n + q > m&&m + q > n)
  {
   interpretationTriangleone(a, b, c);//判断钝角三角形，锐角三角形，钝角三角形，
  }
  if (m + n > q&&n + q > m&&m + q > n)
  {
   interpretationTriangletwo(a, b, c);//判断等腰直角三角形，等边三角形，等腰三角形，
  }
  cout << endl;
  cout << "如果想继续执行，请输入wuluo=666";
  cout << endl;
  cout << "wuluo=";
  cin >> wuluo;
 }
 cout << "结束运行！";
 cout << endl;
}

运行效果：