随机梯度下降（SGD）分类

一、数据导入

1.数据集

MNIST：是一组由美国高中生和人口调查局员工手写的70000个数字的图片。每张图像都用其代表的数字标记。这个数据集被广为使用，因此也被称作是机器学习领域的“Hello World”。

2.导入数据集

from sklearn.datasets import fetch_mldata
mnist=fetch_mldata('MNIST original',data_home='./')

不加data_home参数的话，代码下载的数据集不完整。可以通过其它方法获取mnist-original.mat文件，在当前文件夹下面新建mldata文件夹，并放入.mat文件。下载mnist-original.mat，链接：https://pan.baidu.com/s/1KH27t9hFuGOYnAXgmVgosA 提取码：y1pz 。

>>MNIST
{'COL_NAMES': ['label', 'data'],
 'DESCR': 'mldata.org dataset: mnist-original',
 'data': array([[0, 0, 0, ..., 0, 0, 0],
        [0, 0, 0, ..., 0, 0, 0],
        [0, 0, 0, ..., 0, 0, 0],
        ..., 
        [0, 0, 0, ..., 0, 0, 0],
        [0, 0, 0, ..., 0, 0, 0],
        [0, 0, 0, ..., 0, 0, 0]], dtype=uint8),
 'target': array([ 0.,  0.,  0., ...,  9.,  9.,  9.])}

Scikit-Learn加载的数据集通常具有类似的字典结构，包括：

• DESCR键，描述数据集
• data键，包含一个数组，每个实例为一行，每个特征为一列
• target键，包含一个带有标记的数组

3.测试数据集

共有7万张图片，每张图片有784个特征。因为图片是28X28像素，每个特征代表了一个像素点的强度，从0（白色）到255（黑色）。测试数据集中的一个数字，只需随手抓取一个实例的特征向量，将其重新形成一个28X28数组，然后使用Matplotlib的imshow()函数将其显示出来：

import matplotlib
import matplotlib.pyplot as plt

some_digit=x[36000]
some_digit_image=some_digit.reshape(28,28)

plt.imshow(some_digit_image,cmap=matplotlib.cm.binary,interpolation='nearest')
plt.axis('off')
plt.show()

看起来像一个5，而标签告诉我们没错：

二、准备测试集

MNIST数据集已经分成训练集（前6万张图像）和测试集（最后1万张图像）：

X_train,X_test,y_train,y_test=X[:60000],X[60000:],y[:60000],y[60000:]

将训练集洗牌（保证交叉验证时所有的折叠都差不多）：

import numpy as np
shuffle_index=np.random.permutation(60000)
X_train,y_train=X_train[shuffle_index],y_train[shuffle_index]

三、二元分类器

数字5检测器：区分两个类别：5和非5。
目标向量：

y_train_5=(y_train==5)
y_test_5=(y_test==5)

选择分类器：随机梯度下降（SGD）分类器。
优势：能够有效处理非常大型的数据集，适合在线学习。

创建一个SGDClassifier并在整个训练集上进行训练：

from sklearn.linear_model import SGDClassifier
sgd_clf=SGDClassifier(random_state=42)
sgd_clf.fit(X_train,y_train_5)

检测数字5的图像：

分类器输出一个True，这次猜对了。

四、性能考核

1.使用交叉验证测量精度

K-fold交叉验证法：将训练集分解成K个折叠（子集），然后每次留其中1个折叠进行预测，剩余的折叠用来训练。
用cross_val_score()函数来评估SGDClassifier模型，采用3个折叠：

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf,X_train,y_train_5,cv=3,scoring='accuracy')

所有折叠交叉验证的准确率都超过94%。

2.混淆矩阵

评估分类器性能的更好方法是混淆矩阵。总体思路就是统计A类别实例被分成B类别的次数。
要计算混淆矩阵，需要先有一组预测才能将其与实际目标进行比较，可以使用cross_val_predict()函数：

from sklearn.model_selection import cross_val_predict
y_train_pred=cross_val_predict(sgd_clf,X_train,y_train_5,cv=3)

该函数同样执行K-fold交叉验证，但返回的不是评估分数，而是每个折叠的预测。

要获取混淆矩阵可以使用confusion_matrix()：

from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5,y_train_pred)

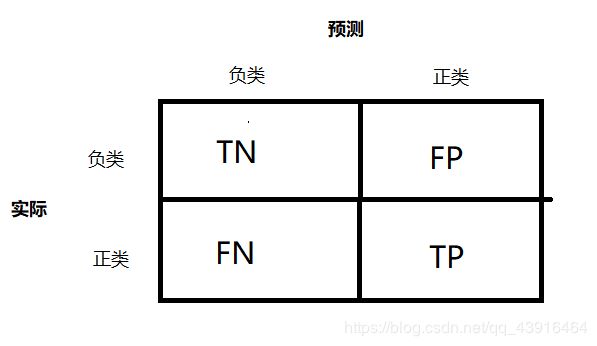
混淆矩阵中的行表示实际类别，列表示预测类别。一个完美的分类器只有真正类和真负类，所以它的混淆矩阵只会在其对角线（左上到右下）上有非零值：

混淆矩阵图解：

3.精度和召回率

精度：分类器正类预测的准确率。
$$精度=\frac{TP}{TP+FP}$$
TP是真正类的数量，FP是假正类的数量。

做一个单独的预测，并确保它是正确的，就可以得到完美精度（精度=1/1=100%）。但这没什么意义，因为分类器会忽略这个正类实例之外的所有内容。因此，精度通常与另一个指标一起使用，这个指标就是召回率（recall），也称为灵敏度（sensitivity）或者真正类率（TPR）：它是分类器正确检测到的正类实例的比率：
$$召回率=\frac{TP}{TP+FN}$$
FN是假负类的数量。

计算精度和召回率：

精度有75%，而召回率只有64%。

精度和召回率可以组合成一个单一的指标，称作F1分数。当你需要一个简单的方法来比较两种分类器时，这是个非常不错的指标。F1分数是精度和召回率的谐波平均值。正常的平均值平等对待所有的值，而谐波平均值会给予较低的值更高的权重。因此，只有当召回率和精度都很高时，分类器才能得到较高的F1分数。
$$F1=\frac{2}{\frac{1}{精度}+\frac{1}{召回率}}=\frac{2\ast 精度\ast 召回率}{精度+召回率}$$
要计算F1分数，只需调用f1_score()即可：

遗憾的是，鱼和熊掌不可兼得：我们不能同时增加精度并减少召回率，反之亦然。这称为精度/召回率权衡。
对于每个实例，SGDClassifier会基于决策函数计算出一个分值，如果该值大于阈值，则将该实例判为正类，否则便将其判为负类。
Scikit-Learn不允许直接设置阈值，但是可以访问它用于预测的分数。可以调用decison_function()方法返回每个实例的分数，然后就可以根据这些分数，使用任意阈值进行预测：

SGDClassifier分类器使用的阈值是0，所以predict()返回的结果是正类，但如果我们提升阈值：

这张图确实是5，当阈值为0时，分类器可以检测到该图，但是当阈值提高到100000时，就错过了这张图。

那么要如何决定使用什么阈值呢？首先，使用cross_val_predict()函数获取训练集中所有实例的分数，但是这次需要它返回的是决策分数而不是预测结果。有了这些分数，可以使用precision_recall_curve()函数来计算所有可能的阈值的精度和召回率。最后，使用Matplotlib绘制精度和召回率相对于阈值的函数图。
Python代码：

y_scores=cross_val_predict(sgd_clf,X_train,y_train_5,cv=3,method='decision_function')
from sklearn.metrics import precision_recall_curve
precisions,recalls,thresholds=precision_recall_curve(y_train_5,y_scores)
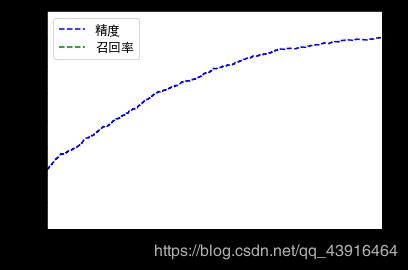
def plot_precision_recall_vs_threshold(precisions,recalls,thresholds):
    plt.plot(thresholds,precisions[:-1],'b--',label='精度')
    plt.plot(thresholds,recalls[:-1],'g--',label='召回率')
    plt.xlabel('阈值')
    plt.legend(loc='upper left')
    plt.ylim([0,1])
plot_precision_recall_vs_threshold(precisions,recalls,thresholds)
plt.show()

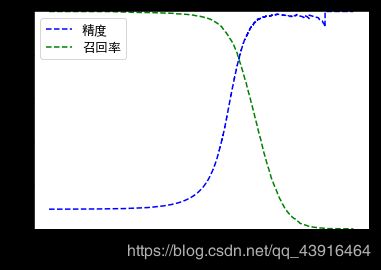
精度曲线比召回率曲线要崎岖一些，原因在于，当你提高阈值时，精度有时也有可能会下降（尽管总体趋势是上升的）。另一方面，当阈值上升时，召回率只会下降，这就解释了为什么召回率的曲线看起来很平滑。
现在，就可以通过轻松选择阈值来实现最佳的精度/召回率权衡了。还有一种找到好的精度/召回率权衡的方法是直接绘制精度和召回率的函数图：

plt.plot(recalls,precisions)
plt.xlabel('召回率')
plt.ylabel('精度')
plt.show()

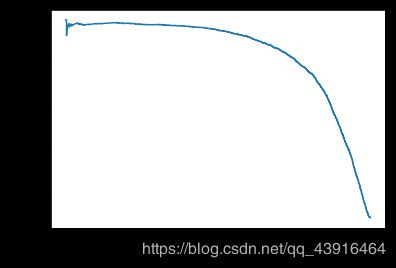
从图中可以看到，从80%的召回率往右，精度开始急剧下降。我们应该尽量在这个陡降之前选择一个精度/召回率权衡——比如召回率60%。

假设我们想要90%的精度目标。通过放大精度和召回率VS阈值图，得出需要使用的阈值大概是50000。要进行预测，除了调用分类器的predict()方法，也可以运行这段代码：

y_train_pred_90=(y_scores>50000)

局部放大图：

可以检查一下这些预测结果的精度和召回率：

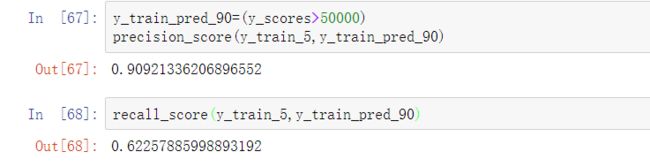
现在我们有一个90%精度的分类器了！由此可见，创建任意一个我们想要的精度的分类器是相当容易的事情：只要阈值足够高即可。然而，如果召回率太低，精度再高，其实也不怎么有用！

4.ROC曲线

还有一种经常与二元分类器一起使用的工具，叫作受试者工作特征曲线（简称ROC）。它与精度/召回率曲线非常相似，但绘制的不是精度和召回率，而是真正类率（TPR）和假正类率（FPR）。FPR是被错误分为正类的负类实例比率。

要绘制ROC曲线，首先需要使用roc_curve()函数计算多种阈值的TPR和FPR。然后，使用Matplotlib绘制FPR对TPR的曲线。
Python代码：

from sklearn.metrics import roc_curve
fpr,tpr,thresholds=roc_curve(y_train_5,y_scores)
def plot_roc_curve(fpr,tpr):
    plt.plot(fpr,tpr,linewidth=2)
    plt.plot([0,1],[0,1],'k--')
    plt.axis([0,1,0,1])
    plt.xlabel('假正类率')
    plt.ylabel('真正类率')
plot_roc_curve(fpr,tpr)
plt.show()

同样这里再次面临一个折中权衡：召回率（TPR）越高，分类器产生的假正类（FPR）就越多。虚线表示纯随机分类器的ROC曲线；一个优秀的分类器应该离这条线越远越好（向左上角）。

有一种比较分类器的方法是测量曲线下面积（AUC）。完美的分类器的ROC AUC等于1，而纯随机分类器的ROC AUC等于0.5。Scikit-Learn提供计算ROC AUC的函数：

• ROC曲线和精度/召回率曲线（PR）的选择：当正类非常少见或者我们更关注假正类而不是假负类时，我们应该选择PR曲线，反之则是ROC曲线。

五、多类别分类器

二元分类器在两个类别中区分，而多类别分类器（也称为多项分类器）可以区分两个以上的类别。

• 一对多（OvA）策略：根据系统要区分的类别数n训练n个二元分类器。然后，当需要对一个样本进行检测分类时，获取每个分类器的决策分数，哪个分类器给分最高，就将其分为哪个类。
• 一对一（OvO）策略：为每一对类别训练一个二元分类器：一个用于区分类别1和类别2，一个区分类别1和类别3，一个区分类别2和类别3，以此类推。如果存在n个类别，那么这需要训练nx(n-1)/2个分类器。当需要对一个样本进行分类时，我们需要运行所有分类器来对图片进行分类，最后看哪个类别获胜最多。OvO的主要优点在于，每个分类器只需要用到部分训练集对其必须区分的两个类别进行训练。

对于大多数二元分类器来说，OvA策略是更好的选择。Scikit-Learn可以检测到我们尝试使用二元分类算法进行多类别分类任务，它会自动运行OvA（SVM分类器除外，它会使用OvO）：

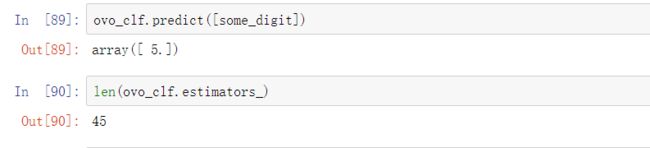
sgd_clf.fit(X_train,y_train)
sgd_clf.predict([some_digit])

这段代码使用原始目标类别0到9在训练集上对SGDClassifier进行训练，而不是以“5”和“剩余”作为目标类别。然后做出预测（类别5）。而在内部，Scikit-Learn实际上训练了10个二元分类器，获得它们对图片的决策分数，然后选择了分数最高的类别。

想知道是不是这样，可以调用decision_function()方法。它会返回10个分数，每个类别1个，而不再是每个实例返回1个分数：

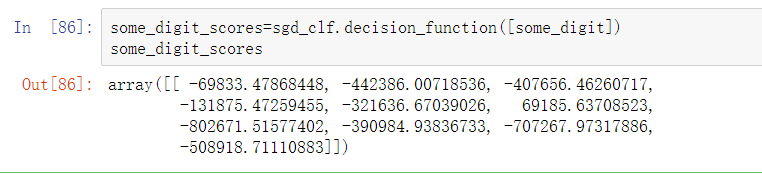
当训练分类器时，目标类别的列表会存储在classes_这个属性中，按值的大小排序：

如果想要强制Scikit-Learn使用一对一或一对多策略，可以使用OneVsOneClassifier或OneVsRestClassifier类。只需要创建一个实例，然后将二元分类器传给其构造函数。例如，使用OvO策略，基于SGDClassifier创建一个多类别分类器，代码如下：

from sklearn.multiclass import OneVsOneClassifier
ovo_clf=OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train,y_train)

看下预测结果和内部分类器数：

六、错误分析

对一个潜有力的模型进一步改进，方法之一就是分析其错误类型。首先，看看混淆矩阵：

y_train_pred=cross_val_predict(sgd_clf,X_train,y_train,cv=3)
conf_mx=confusion_matrix(y_train,y_train_pred)

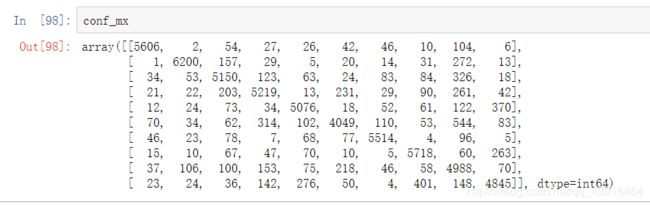
数字有点多，使用Matplotlib的matshow()函数来查看混淆矩阵的图像表示，通常更加方便：

plt.matshow(conf_mx,cmap=plt.cm.gray)
plt.show()

混淆矩阵看起来很不错，因为大多数图片都在主对角线上，这说明它们被正确分类。数字5看起来比其他数字稍暗一些，这可能意味着数据集中数字5的图片较少，也可能是分类器在数字5上的执行效果不如在其他数字上好。

让我们把焦点放在错误上。首先，我们需要将混淆矩阵中的每个值除以相应类别中的图片数量，这样我们比较的就是错误率而不是错误的绝对值（后者对图片数量较多的类别不公平），用0填充对角线，只保留错误，重新绘制结果：

row_sums=conf_mx.sum(axis=1,keepdims=True)
norm_conf_mx=conf_mx/row_sums
np.fill_diagonal(norm_conf_mx,0)
plt.matshow(norm_conf_mx,cmap=plt.cm.gray)
plt.show()

现在，我们可以清晰地看到分类器产生的错误种类了。每行代表实际类别，每列表示预测类别。
第8列和第9列整体看起来非常亮，说明有许多图片被错误地分类为数字8或数字9了。同样，类别8和类别9的行看起来也偏亮，说明数字8和数字9经常会跟其他数字混淆。

分析混淆矩阵通常可以帮助我们深入了解如何改进分类器。通过上面那张图来看，我们的精力可以花在改进数字8和数字9的分类，以及修正数字5和数字8的混淆上。例如，可以试着收集更多这些数字的训练数据。