一种智能车控制算法的设计和实现
1 巡线控制算法
1.1 运动模型
智能车的运动控制是通过控制驱动马达和伺服舵机实现的。在理想情况下,可以认为4个轮胎绕着同一个圆心做纯滚动,其离散运动模型公式为:
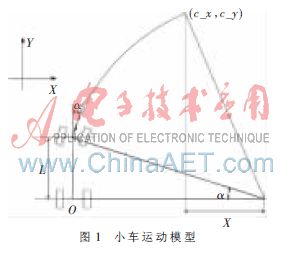
其中V是线速度,W为角速度, x(t)、y(t)为小车的坐标,angle(t)为智能车的方向角(以小车前进方向为起始线,逆时针为正),Δt为采样周期。模型如图1所示。
由于模型车的运动速度较高,在行驶过程中轮胎与赛道会发生一定侧滑,因此还需要引进侧滑修正。
1.2 舵机控制
方向控制是控制策略的难点。传统的PID算法[1,2]不需要对控制对象做细致分析,只需根据控制效果对参数进行调整[3].但由于控制器的输入量均对输出量产生影响,且高度耦合,很难根据控制效果准确地对参数进行修正,因此参数的整定工作十分繁重。此外,当车的状态不同时(如低速和高速时),最佳参数也有很大不同,这给进一步调试带来了困难。
本文采用"最优曲率法".控制思想是:模型车在一个控制周期内的运动轨迹可以近似为一段圆弧,整个运动轨迹可以看做由小段圆弧连接成的曲线。在假设线速度恒定的前提下,给定路径上的一个点就能确定出智能车到达该点所应具有的舵机角度[4].在每个控制周期内选择路径上的一点(或若干点),根据预先建立的圆弧运动模型计算出模型车在接下来的一个(或若干个)运动周期内要到达选定点所需的理想状态,此时该控制周期的输出量就是在未来几个控制周期内使模型车的实际状态尽可能逼近理想状态的控制量。
以车的后桥中点为原点建立坐标系,车的中轴为y轴,其正向为车的前方。设(c_x,c_y)为路径上的点在该坐标系中的坐标。则控制量的计算公式为[5]:
这种方法在车速较低时可以取得很好的效果,当车速较高时,有很多因素对控制效果的影响会显著增大,需要作出适当的补偿。其中主要因素是控制量的实际输出时刻与理想输出时刻的延时,这个延时是由图像处理和控制量的计算都需要一定时间造成的。对此,本文采取的方法是根据车的当前状态估算出控制量的输出时刻的路径信息,用这个路径信息计算控制量。
另一个重要因素是侧滑。智能车在行驶过程中存在侧滑,可以通过侧滑角作补偿。设车轮的角度为θ,加入侧滑后的等效车轮角度为θ′,本文假设二者符合如下关系:
还有一个重要因素是,当车速较高时,舵机的响应速度相对较慢。要克服这个问题,应使舵机提前做出反应。因此需要在控制器的输出量中引入路径的趋势。本文用前瞻点处的斜率k表示路径的趋势,在原控制量θ的基础上增加一个与路径趋势相关的分量θ″=para×v×k,其中para通过实验结果自动调整,如果需要,可以将para设为和其他变量相关的函数。
经过上述改进之后,最优曲率法在车速较高的时候依然能够取得很好的控制效果。此部分程序流程图如图3所示。
该算法的优点是参变量较少,且相互间的耦合很小,对控制效果的影响较为独立,可以根据实验结果快速确定调整量。只要对参数进行适当调整,就能取得较好的控制效果。
1.3 速度控制
在速度决策方面,首先尝试了基于有效前瞻的速度控制[6],即v=基准值+有效前瞻量×系数。这个策略的好处是简单有效。但事实上智能车通过路线的最佳速度和前瞻量并不呈简单的线性关系。如果处于弯道中,尤其是"十"字弯中时,由于车的阻力增大,车速也大大下降,同时由于车体运行较稳定,车轮不会发生大幅度转向,侧滑的风险很小,这时可以提速;当出弯时,如果检测或预测到前方较平缓,可以放心加速。由于局部快不一定整体快,因此还要做好衔接,使得整个跑的过程中各速度间过渡圆滑。基于这些想法,本文在前面的速度决策上做了改进,在保证安全性的前提下提高了整体速度。
1.4 仿真调试
为了便于分析控制效果,本文搭建了一个Matlab仿真环境。在这个仿真环境中,车模的参数和动态响应特性都是参照实验结果设计的,并引入了侧滑、延时、舵角死区等很多干扰因素,可以在很大程度上反映算法的真实情况。仿真界面如图4所示。
在实际的调试过程中,本文首先在仿真环境下设计算法,并分析模型车通过各种跑道时所需要的理想的舵机角度,测试通过后将算法移植到模型车上。如果实际控制效果与仿真结果差别较大,则将控制算法的执行情况与理想情况下的期望值进行比较,针对差别有目的地作出改进。这在很大程度上提高了调试效率。
2 贪婪路径规划
2.1 优化问题
优化问题中有两个约束条件:
(1)车不出边界。
(2)小车行驶路径最短。主要是弯道切弯行驶,大小S弯走最优路径。
对于一般问题,全局最优解是最好的结果,但是智能小车行驶的跑道是随机的,并且小车传感器获得的道路信息有限,要得到全局最优解很困难,所以根据贪婪算法思想,在局部的每一点获得最优解来逼近全局最优解。贪婪路径规划就是给出一些小车行驶路径点,保证小车行驶时最大程度地满足以上两个优化条件。
2.2 最优解分析求解
比赛用的路径只有两种:直道和圆弧道。关键在圆弧道,分单圆弧道和多圆弧道,单圆弧道指衔接两个直道的一个弯道,多圆弧道指S形弯道。
首先,分析单圆弧。单圆弧示意图如图5所示,已知路径宽为60 cm,T点为小车传感器识别出的最远前瞻路径点。
如果车向着T点行驶去,车有可能超出跑道。所以需要计算出最远前瞻点和车头连线(OT)与路径圆弧线(弧OT)之间的最远距离D,如果D超出20 cm(车模宽20 cm,当车模恰好压跑道边时,车模中心与路径线的距离是20 cm),就不满足约束条件(1)。
当D超出20 cm时,可以将前瞻点T后移,计算出使D=20 cm的T′点,如图5所示。在给出的直线上根据小车的速度可以选取一点作为贪婪规划的解路径点。速度快时,选点前移,反之后移。
其次,对于多圆弧S形道,需要找到两个圆弧的连接点,称为转折点。图6中T点为转折点。S形道路与一般弯道路径不同,不能用单圆弧的方法求出最优路径点,因为最远前瞻点可能跨两个圆弧,求取距离D困难,最重要的是用单圆弧的方法利用最远前瞻点求出的解不是最优的解。可以发现在圆弧转折点前面的圆弧(弧OT)是一个单圆弧,用这段单圆弧来求解才是合理的。利用最小二乘法可以对每一个点求出一个斜率,其中转折点的特点是转折点是斜率曲线的极值点。可以发现,对于90°小S弯,D等于14.65 cm,小车直线通过,而120°中等S弯,D等于25 cm.
需要注意,由于传感器的视野和图像处理的限制,有时最远前瞻点只能取到N点,如图5所示。这时可以使用广角镜头(实验中选取焦距f=2.8 mm)扩大视野,提高图像处理算法的精度来使前瞻点尽量靠前,到达T附近。
本文根据转向模型,提出了"最优曲率"算法及"贪婪路径规划"算法。实验表明,这两种算法结合起来能使小车更安全、快速地行驶,可作为除PID算法和模糊控制算法以外的第三种选择。
原文地址:http://www.dzsc.com/data/html/2011-7-8/90722.html